Circuits - College Physics
Card 0 of 12
A parallel plate capacitor with no dielectric has capacitance 
. The distance between the capacitor plates is halved. What is the new capacitance?
A parallel plate capacitor with no dielectric has capacitance
The capacitance of a parallel plate capacitor is proportional to the inverse of the distance between the plates. If the distance is halved, the capacitance is doubled.
The capacitance of a parallel plate capacitor is proportional to the inverse of the distance between the plates. If the distance is halved, the capacitance is doubled.
Compare your answer with the correct one above
An RC circuit is connected to a 
power supply. If the resistance of the resistor is 
and the capacitance is 
, how long will it take for this capacitor to become fully charged?
An RC circuit is connected to a
The formula for finding the voltage of a simple RC circuit is
, where 
is the capacitor voltage, 
is the source voltage, 
is the resistance, and 
is the capacitance.
We want to know when the capacitor will reach the voltage of the power source 
so
and thus 
Using the properties of natural logs yields
Solving for 
yields 
The formula for finding the voltage of a simple RC circuit is
We want to know when the capacitor will reach the voltage of the power source
Using the properties of natural logs yields
Solving for
Compare your answer with the correct one above
Which of the following expressions gives the capacitance for a capacitor in a circuit in which the only factors known are a) the current through the circuit, b) the resistance of the circuit, and c) the charge that has accumulated on the capacitor?
Which of the following expressions gives the capacitance for a capacitor in a circuit in which the only factors known are a) the current through the circuit, b) the resistance of the circuit, and c) the charge that has accumulated on the capacitor?
In this question, we're given a number of parameters of a circuit and are asked to find how we can use these various parameters to show the capacitance of the circuit's capacitor.
First, recall what a capacitor is; something that stores charge for a given voltage difference. In other words, when there is a voltage difference between the two plates of a capacitor, a certain amount of charge can be stored on these plates. The more charge that can be stored for a given voltage difference, the greater that capacitor's capacitance. This can be shown by the following equation.
From the above expression, 
is the capacitance which we are trying to find a proper expression for. 
is the charge accumulated on the plates, which is one parameter we're given. Voltage, 
, on the other hand, is not provided.
To put the voltage into different terms, we'll need to use Ohm's law, which states the following.
In other words, the voltage is proportional to both the current and the resistance of the circuit.
Since we are given both current and resistance as known parameters in the question stem, we can use these for our final answer. By substituting the 
in the capacitance expression with 
, we obtain the following answer.
In this question, we're given a number of parameters of a circuit and are asked to find how we can use these various parameters to show the capacitance of the circuit's capacitor.
First, recall what a capacitor is; something that stores charge for a given voltage difference. In other words, when there is a voltage difference between the two plates of a capacitor, a certain amount of charge can be stored on these plates. The more charge that can be stored for a given voltage difference, the greater that capacitor's capacitance. This can be shown by the following equation.
From the above expression,
To put the voltage into different terms, we'll need to use Ohm's law, which states the following.
In other words, the voltage is proportional to both the current and the resistance of the circuit.
Since we are given both current and resistance as known parameters in the question stem, we can use these for our final answer. By substituting the
Compare your answer with the correct one above
What size resistor should be connected across the terminals of a 
battery to produce a current of 
?
What size resistor should be connected across the terminals of a
Ohm's law is 
.
In this case, 
and 
.
Solving for the resistance, 
, we get:
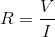
Substitute known values and solve for the unknown resistance:
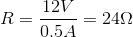
Ohm's law is
In this case,
Solving for the resistance,
Substitute known values and solve for the unknown resistance:
Compare your answer with the correct one above
A 
battery is connected to a small heater with constant resistance 
. How much current flows through the heater?
A
Ohm's law relates voltage to current and resistance, 
. To find the current, we simply divide the voltage by the resistance and get 
Ohm's law relates voltage to current and resistance,
Compare your answer with the correct one above
The picture below shows the electron energy levels of a hydrogen atom.
If an electron is excited to the 5th energy level, how many different transitions can it make to return to ground state?
The picture below shows the electron energy levels of a hydrogen atom.
If an electron is excited to the 5th energy level, how many different transitions can it make to return to ground state?
Electrons don't always drop from the top to the bottom, sometimes they can make 2 or more transitions during the journey. For example, it could drop to the n=4 then to the n=1 levels. Or n=4 to n=2 then n=1. So when you count up all the possible transitions that can be made between n=5 and n=1, you get 10.
Electrons don't always drop from the top to the bottom, sometimes they can make 2 or more transitions during the journey. For example, it could drop to the n=4 then to the n=1 levels. Or n=4 to n=2 then n=1. So when you count up all the possible transitions that can be made between n=5 and n=1, you get 10.
Compare your answer with the correct one above
Use this circuit diagram for the next question.
What is the current traveling through the R2 resistor?
Use this circuit diagram for the next question.
What is the current traveling through the R2 resistor?
So this problem has several steps to it. We need to think backwards. Ultimately we need to know the current going through R2. We will be using Ohms law so we need to know the voltage going through just that resistor.
Because it is in parallel with R3 and R4, all three must have the same voltage. However since it is in series with 2 other resistors, it will not be the voltage from the battery.
Lets reduce the parallel circuit to 1 resistor. Using the formula
, then remembering to invert the answer yields
.
That resistance is in series with R1 and R5 so to find the current going through each of them we need to add the resistances and use Ohm's law again.
Doing so yields a current of 
. This is the current going through the circuit. Now we can find the voltage drop of just our equivalent parallel resistor.
.
So all three of the resistors that are in parallel have a voltage of 
going through them.
Now we can go all the way back to the R3 resistor knowing that it has a resistance of 
and a voltage of 
. Use Ohm's Law one more time to solve for the current of the R3 resistor.
So this problem has several steps to it. We need to think backwards. Ultimately we need to know the current going through R2. We will be using Ohms law so we need to know the voltage going through just that resistor.
Because it is in parallel with R3 and R4, all three must have the same voltage. However since it is in series with 2 other resistors, it will not be the voltage from the battery.
Lets reduce the parallel circuit to 1 resistor. Using the formula
That resistance is in series with R1 and R5 so to find the current going through each of them we need to add the resistances and use Ohm's law again.
Doing so yields a current of
So all three of the resistors that are in parallel have a voltage of
Now we can go all the way back to the R3 resistor knowing that it has a resistance of
Compare your answer with the correct one above
Suppose that a circuit with a single resistor is connected to a 
battery. If 
of power is generated across this resistor, what is its resistance?
Suppose that a circuit with a single resistor is connected to a
For this problem, let's first take note of what we know and what we don't. We're given voltage and power, but we're not given resistance or current. Since we have two unknowns, we're going to need two equations.
One of the equations that we can use is the power generated by current flowing through a resistor.
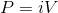
In addition, we also need to use Ohm's law.
With these two equations in mind, we can relate them to one another by isolating the variable for current in one equation and then substituting it into the other one.
Manipulating Ohm's law:
Then substituting this into the power equation:
And rearranging to isolate the variable for resistance:
Now we just need to plug in the values from the question stem to obtain the answer:
For this problem, let's first take note of what we know and what we don't. We're given voltage and power, but we're not given resistance or current. Since we have two unknowns, we're going to need two equations.
One of the equations that we can use is the power generated by current flowing through a resistor.
In addition, we also need to use Ohm's law.
With these two equations in mind, we can relate them to one another by isolating the variable for current in one equation and then substituting it into the other one.
Manipulating Ohm's law:
Then substituting this into the power equation:
And rearranging to isolate the variable for resistance:
Now we just need to plug in the values from the question stem to obtain the answer:
Compare your answer with the correct one above
A resistive heating element can be modeled as a resistor connected across the terminals of a battery.
If the battery is selected to be 
, what should the resistance of the heating element be if the radiated power is to total 
?
A resistive heating element can be modeled as a resistor connected across the terminals of a battery.
If the battery is selected to be
We are asked to calculate the power dissipated through a resistor connected to a battery. We know that 
. Substituting the values given above, 
. Solving for R yields 
.
We are asked to calculate the power dissipated through a resistor connected to a battery. We know that
Compare your answer with the correct one above
What is the RMS voltage of a 
peak-to-peak AC current?
What is the RMS voltage of a
This question requires two steps: the first is to calculate the peak voltage of the AC current, and the second requires conversion of the peak voltage to an RMS voltage. We are told that the current is 
peak-to-peak. Thus, the peak voltage is half of this, or 
. By definition, to convert peak voltage to RMS voltage, we must divide the peak voltage by 
:
This question requires two steps: the first is to calculate the peak voltage of the AC current, and the second requires conversion of the peak voltage to an RMS voltage. We are told that the current is
Compare your answer with the correct one above
A 
battery is connected to two 
light bulbs that are arrange in parallel. What is the total power dissipated by the light bulbs?
A
The power dissipated in each light bulb is 
. Since there are two light bulbs, the total power dissipated is 
The power dissipated in each light bulb is
Compare your answer with the correct one above
You are given three resistors with known values:
You are asked to create a circuit with a total resistance of between 
and 
. How should you arrange the resistors to accomplish this?
You are given three resistors with known values:
You are asked to create a circuit with a total resistance of between
This question requires no math to correctly answer! You should not need to 'brute force' it. Although it is designed to appear time consuming, it should be relatively easily once the principle of resistors in parallel is understood. Whenever two resistors are connected in parallel, the net resistance must be less than the resistance of either of the two alone. When resistors are connected in series, the net resistance must be more than the resistance of either alone.
Explanation of correct answer:
and 
in parallel, connected to 
in series - It is possible to 'eyeball' this to see that this is at least feasible. 
and 
in parallel must make a network with an overall resistance less than 
. When added in series with 
(
), the overall may fall between 
and 
. To confirm, one could do the math to calculate the overall resistance, but the point of this question is to use general principles to quickly eliminate the other, incorrect answer choices.
Explanations of incorrect answers:
, 
, and 
in parallel - This combination cannot possibly work since the overall resistance must be less than 
(the smallest resistor in parallel).
and 
in parallel, connected to 
in series - Regardless of the overall resistance of 
and 
in parallel, the connection with 
in series makes the total resistance more than 
.
and 
in parallel; 
is not necessary - Placing 
and 
in parallel must result in a resistance less than 
.
, 
, and 
in series - Connecting resistors in series results in an overall resistance greater than that of any one alone. Since 
and 
are included in series, the sum of the resistances is obviously much greater than what we are asked to produce and this choice can be immediately eliminated.
This question requires no math to correctly answer! You should not need to 'brute force' it. Although it is designed to appear time consuming, it should be relatively easily once the principle of resistors in parallel is understood. Whenever two resistors are connected in parallel, the net resistance must be less than the resistance of either of the two alone. When resistors are connected in series, the net resistance must be more than the resistance of either alone.
Explanation of correct answer:
Explanations of incorrect answers:
Compare your answer with the correct one above