Solving Equations and Inequallities - College Algebra
Card 0 of 20
Solve the following

Solve the following
We have to set up two equations, which are.


Now lets solve for x in each equation.




So the solutions are  and
and 
We have to set up two equations, which are.
Now lets solve for x in each equation.
So the solutions are 
Compare your answer with the correct one above
Solve:

Solve:
We need to set up two equations since we are dealing with absolute value

We solve for  , in each equation to get the solutions.
, in each equation to get the solutions.


We need to set up two equations since we are dealing with absolute value
We solve for 
Compare your answer with the correct one above
Solve:

Solve:
We need to set up two equations since we are dealing with absolute value

We solve for  , in each equation to get the solutions.
, in each equation to get the solutions.


We need to set up two equations since we are dealing with absolute value
We solve for 
Compare your answer with the correct one above
Solve the following:

Solve the following:
To solve, you must split the absolute value into the two following equations.
 and
and 
Now, solve for x and right it in interval form.



To solve, you must split the absolute value into the two following equations.

Now, solve for x and right it in interval form.
Compare your answer with the correct one above
Solve the following equation for  .
.

Solve the following equation for 
We first need to get rid of the absolute value symbol to solve the equation. TO break this absolute value, we assign two values to the right hand side, as shown below.


We now proceed to solve each equation independently.
Starting with the first equation, we get


Now for the second equation,


We first need to get rid of the absolute value symbol to solve the equation. TO break this absolute value, we assign two values to the right hand side, as shown below.
We now proceed to solve each equation independently.
Starting with the first equation, we get
Now for the second equation,
Compare your answer with the correct one above
Simplify the radical:

Simplify the radical:
To simplify the radical, break the radical in the numerator down into its factors. When doing so, the radical in the bottom will call with one from the numerator.

To simplify the radical, break the radical in the numerator down into its factors. When doing so, the radical in the bottom will call with one from the numerator.
Compare your answer with the correct one above
Solve the following equation:

Solve the following equation:
To solve for  first isolate the absolute value portion on one side of the equation and all other constants on the other side.
first isolate the absolute value portion on one side of the equation and all other constants on the other side.



Recall that the absolute value can come from either a negative or positive value therefore two possible equations are set up.



To solve for 
Recall that the absolute value can come from either a negative or positive value therefore two possible equations are set up.
Compare your answer with the correct one above
Solve the equation:

Solve the equation:
To solve for  first isolate the absolute value portion on one side of the equation and all other constants on the other side.
first isolate the absolute value portion on one side of the equation and all other constants on the other side.


Since absolute values can come from either negative or positive values, two equations need to be set up and solved for.



To solve for 
Since absolute values can come from either negative or positive values, two equations need to be set up and solved for.
Compare your answer with the correct one above
Solve for x:

Solve for x:
To solve  we need to find a way to reverse the operation of taking the absolute value. What we need to do is think about what the absolute value operation does to an expression. Since it makes everything positive,
we need to find a way to reverse the operation of taking the absolute value. What we need to do is think about what the absolute value operation does to an expression. Since it makes everything positive,  . So actually solving the original equation comes down to solving the following two equations:
. So actually solving the original equation comes down to solving the following two equations:


So we get the two solutions as:


To solve 

So we get the two solutions as:
Compare your answer with the correct one above
Solve the inequality:

Solve the inequality:
To solve for  first isolate the absolute value portion on one side of the equation and all other constants on the other side.
first isolate the absolute value portion on one side of the equation and all other constants on the other side.


Since absolute values can come from either negative or positive values, two equations need to be set up and solved for.



To solve for 
Since absolute values can come from either negative or positive values, two equations need to be set up and solved for.
Compare your answer with the correct one above
Solve: 
Solve:
Add  on both sides.
on both sides.


Add 8 on both sides.


Divide by two on both sides.

The answer is: 
Add 
Add 8 on both sides.
Divide by two on both sides.
The answer is:
Compare your answer with the correct one above
Quadratic equations appear often in physics. The basic kinematic equations for the position  of a particle as a function of time
of a particle as a function of time  , with an initial velocity
, with an initial velocity  (a constant) and constant acceleration
(a constant) and constant acceleration  can be written as,
can be written as,

This is a quadratic function in  . The function therefore gives the position as a quadratic function of time
. The function therefore gives the position as a quadratic function of time  . If we are dealing with a free-falling object under Earth's gravitational field, we might write this function in the form,
. If we are dealing with a free-falling object under Earth's gravitational field, we might write this function in the form,
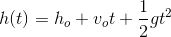
to express the "height"  of the object at a given time
of the object at a given time  falling with a constant acceleration
falling with a constant acceleration  . Here
. Here  the initial height (a constant). The units for acceleration are meters-per-square second
the initial height (a constant). The units for acceleration are meters-per-square second  . The negative acceleration is a convention to signify that the direction of the acceleration is downward.
. The negative acceleration is a convention to signify that the direction of the acceleration is downward.
Find the time required for a ball dropped from a height of 100 m from rest to reach the ground using the quadratic function for height written below,
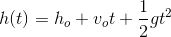
(Hint, what is the value of the height  when the ball strikes the ground?).
when the ball strikes the ground?).
Quadratic equations appear often in physics. The basic kinematic equations for the position 



This is a quadratic function in 

to express the "height" 




Find the time required for a ball dropped from a height of 100 m from rest to reach the ground using the quadratic function for height written below,
(Hint, what is the value of the height 
We're given the function,

We know that the gravitational acceleration on earth is:
 (meters-per-square second)
(meters-per-square second)
Because the ball starts at rest, the initial velocity  is zero,
is zero,
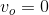 (meters-per-second)
(meters-per-second)
We are given the initial height,
 (meters)
(meters)
When the ball reaches the ground, the height is "zero," so the value of  is zero at this time, and so we have:
is zero at this time, and so we have:
 (units omitted in the equation).
(units omitted in the equation).
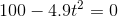


(Note that although taking the square root of both sides of an equation will produce positive and negative solutions, we ignore the negative solution since "negative time" makes no sense in the context of this problem).
We're given the function,
We know that the gravitational acceleration on earth is:

Because the ball starts at rest, the initial velocity 
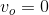
We are given the initial height,

When the ball reaches the ground, the height is "zero," so the value of 

(Note that although taking the square root of both sides of an equation will produce positive and negative solutions, we ignore the negative solution since "negative time" makes no sense in the context of this problem).
Compare your answer with the correct one above
A sidewalk on a street corner reaches from a library to a bookstore making an L shape around that corner. The L shaped path has one length that is twice as long as the other. The diagonal path being built between the two buildings will be 102 feet long. How many feet shorter is the diagonal path than the traditional L shaped path around the corner?
A sidewalk on a street corner reaches from a library to a bookstore making an L shape around that corner. The L shaped path has one length that is twice as long as the other. The diagonal path being built between the two buildings will be 102 feet long. How many feet shorter is the diagonal path than the traditional L shaped path around the corner?
Use Pythagorean Theorem to solve.
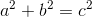



Since the path around the corner is 3x, 3 times the  is approximately 137. The distance saved is 137-102= 35 feet. Note that we only needed the positive square root since we cannot have a negative distance.
is approximately 137. The distance saved is 137-102= 35 feet. Note that we only needed the positive square root since we cannot have a negative distance.
Use Pythagorean Theorem to solve.
Since the path around the corner is 3x, 3 times the 
Compare your answer with the correct one above
Solve 
Solve
To make this problem easier, lets start off by doing a u-substitution.
Let  .
.


Now we can factor the left hand side.

We have two solutions for  , now we can plug those into
, now we can plug those into  , to get all the solutions.
, to get all the solutions.


To make this problem easier, lets start off by doing a u-substitution.
Let 
Now we can factor the left hand side.
We have two solutions for 

Compare your answer with the correct one above
Find all real roots of the polynomial function

Find all real roots of the polynomial function
Find the roots of the polynomial,

Set  equal to
equal to 

Factor out  ,
,

Notice that the the factor  is a quadratic even though it might not seem so at first glance. One way to think of this is as follows:
is a quadratic even though it might not seem so at first glance. One way to think of this is as follows:
Let 
Then we have  , substitute into
, substitute into  to get,
to get,

Notice that the change in variable from  to
to  has resulted in a quadratic equation that can be easily factored due to the fact that it is a square of a simple binomial:
has resulted in a quadratic equation that can be easily factored due to the fact that it is a square of a simple binomial:

The solution for  is,
is,

Because  we go back to the variable
we go back to the variable  ,
,

Therefore, the roots of the  factor are,
factor are,

The other root of  is
is  since the function clearly equals
since the function clearly equals  when
when  .
.
The solution set is therefore, 
Below is a plot of  . You can see where the function intersects the
. You can see where the function intersects the  -axis at points corresponding to our solutions.
-axis at points corresponding to our solutions.

Further Discussion
The change of variable was a tool we used to write the quadratic factor in a more familiar form, but we could have just factored the original function in terms of  as follows,
as follows,




Setting this to zero gives the same solution set, 
Find the roots of the polynomial,
Set 
Factor out 
Notice that the the factor 
Let
Then we have 

Notice that the change in variable from 

The solution for 
Because 

Therefore, the roots of the 
The other root of 



The solution set is therefore,
Below is a plot of 

Further Discussion
The change of variable was a tool we used to write the quadratic factor in a more familiar form, but we could have just factored the original function in terms of 
Setting this to zero gives the same solution set,
Compare your answer with the correct one above
Give the complete solution set for the equation:

Give the complete solution set for the equation:

can be rewritten in quadratic form by setting  , and, consequently,
, and, consequently,  ; the resulting equation is as follows:
; the resulting equation is as follows:

By the reverse-FOIL method we can factor the trinomial at left. We are looking for two integers with sum 8 and product 12; they are 2 and 6, so the equation becomes

Setting both binomials equal to 0, it follows that
 or
or  .
.
Substituting  for
for  , we get
, we get
 ,
,
in which case
 ,
,
or 
in which case
 .
.
The solution set is  .
.
can be rewritten in quadratic form by setting 

By the reverse-FOIL method we can factor the trinomial at left. We are looking for two integers with sum 8 and product 12; they are 2 and 6, so the equation becomes
Setting both binomials equal to 0, it follows that


Substituting 


in which case

or
in which case

The solution set is 
Compare your answer with the correct one above
Give the complete set of real solutions for the equation:

Give the complete set of real solutions for the equation:

can be rewritten in quadratic form by setting  , and, consequently,
, and, consequently,  ; the resulting equation is as follows:
; the resulting equation is as follows:

By the reverse-FOIL method we can factor the trinomial at left. We are looking for two integers with sum 8 and product 12; they are  and
and  , so the equation becomes
, so the equation becomes

Setting both binomials equal to 0, it follows that
 or
or  .
.
Substituting  for
for  , we get
, we get

in which case
 ,
,
and
 ,
,
in which case

The set of real solutions is therefore  .
.
can be rewritten in quadratic form by setting 

By the reverse-FOIL method we can factor the trinomial at left. We are looking for two integers with sum 8 and product 12; they are 

Setting both binomials equal to 0, it follows that


Substituting 

in which case

and

in which case
The set of real solutions is therefore 
Compare your answer with the correct one above
Solve for X:

Solve for X:
In  , if we're solving for x, we first need to get the "x" term isolated. We do this by subtracting 3 from both sides so:
, if we're solving for x, we first need to get the "x" term isolated. We do this by subtracting 3 from both sides so:

becomes

Now we divide both sides by 8

Re-written the answer becomes

In 
becomes
Now we divide both sides by 8
Re-written the answer becomes
Compare your answer with the correct one above
Larry has a handful of dimes and quarters. In total, he has 14 coins with a value of $2.60. How many of each coin does he have?
Larry has a handful of dimes and quarters. In total, he has 14 coins with a value of $2.60. How many of each coin does he have?
Since this problems has 2 variables (D-dimes and Q-quarters) we need 2 equations. Because Larry has 14 coins, the first equation can be written as:

The value of those coins equals $2.60 or 260 cents. If Dimes are worth 10C and quarters are 25C, the next equation can be written as

To solve this write both equations on top of each other


Now we eliminate 1 variable by multiplying 1 equation by the lowest common denominator (as a negative) and adding the equations together.
 becomes
becomes

adding the equations


-----------------------------------

now we solve for Q.

Since we know Q, now we plug it back in to an equation and find D

Larry has 6 dimes and 8 quarters
Since this problems has 2 variables (D-dimes and Q-quarters) we need 2 equations. Because Larry has 14 coins, the first equation can be written as:
The value of those coins equals $2.60 or 260 cents. If Dimes are worth 10C and quarters are 25C, the next equation can be written as
To solve this write both equations on top of each other
Now we eliminate 1 variable by multiplying 1 equation by the lowest common denominator (as a negative) and adding the equations together.

adding the equations
-----------------------------------
now we solve for Q.
Since we know Q, now we plug it back in to an equation and find D
Larry has 6 dimes and 8 quarters
Compare your answer with the correct one above
The town of Marysville is hosting its annual festival. For admission tickets, adults are charged $8, and children are charged $4. The town sold 2300 tickets and took in $13,688 in total ticket revenue. How many more children were admitted to the festival than adults?
The town of Marysville is hosting its annual festival. For admission tickets, adults are charged $8, and children are charged $4. The town sold 2300 tickets and took in $13,688 in total ticket revenue. How many more children were admitted to the festival than adults?
This question requires setting up two equations and then solving the system of two equations. One equation represents the total number of tickets sold, and the other equation represents the total revenue. Both equations will use the same two variables,  and
and  , for the number of children and adults who were admitted, respectively.
, for the number of children and adults who were admitted, respectively.
The first equation is the easier of the two. The sum of the number of children and the number of adults admitted to the fair will equal 2300.

The second equation will incorporate the price charged to children and adults
Children's tickets cost $4 and adults' tickets cost $8. The total amount of money raised was $13,688.

To solve the system of equations, you can eliminate one of the variables. One way to do this is via the elimination method. To eliminate 

Now add the two equations together to eliminate a variable.


--------------------------------

Solve for  .
.

Substitute  into either of the original equations and solve for
into either of the original equations and solve for  .
.


There were 1178 children and 1122 adults admitted to the festival. Finally, subtract the results.

This question requires setting up two equations and then solving the system of two equations. One equation represents the total number of tickets sold, and the other equation represents the total revenue. Both equations will use the same two variables, 

The first equation is the easier of the two. The sum of the number of children and the number of adults admitted to the fair will equal 2300.
The second equation will incorporate the price charged to children and adults
Children's tickets cost $4 and adults' tickets cost $8. The total amount of money raised was $13,688.
To solve the system of equations, you can eliminate one of the variables. One way to do this is via the elimination method. To eliminate
Now add the two equations together to eliminate a variable.
--------------------------------
Solve for 
Substitute 

There were 1178 children and 1122 adults admitted to the festival. Finally, subtract the results.
Compare your answer with the correct one above










