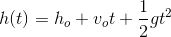College Algebra - Solving Equations and Inequallities

1

Solve:

2

Solve the inequality:

$8+\left | 4x-7\right |\geq17$

3

Solve:

4

Solve for X and Y with the following set of equations:

5

Solve the following equation for .

$\left |x^2-8 \right |=1$

6

Solve the following:

$\left | x-2 \right |>1$

7

Solve:

8

Solve the equation:

$-5\left | 4+2x\right |=-100$

9

Quadratic equations appear often in physics. The basic kinematic equations for the position of a particle as a function of time , with an initial velocity (a constant) and constant acceleration can be written as,

$x(t)=x_o +v_ot+\frac{1}{2}at^2$

This is a quadratic function in . The function therefore gives the position as a quadratic function of time . If we are dealing with a free-falling object under Earth's gravitational field, we might write this function in the form,

$h(t)=h_o +v_ot +\frac{1}{2}gt^2$

to express the "height" of the object at a given time falling with a constant acceleration . Here the initial height (a constant). The units for acceleration are meters-per-square second . The negative acceleration is a convention to signify that the direction of the acceleration is downward.