Solving for Time - CLEP Calculus

Card 0 of 20

Question

The position of a particle is defined by s(t) = 4t3 – 3t2 + 2t. At what time (to the nearest hundreth) is its velocity equal to 384?

Answer

The position of a particle is defined by s(t) = 4t3 – 3t2 + 2t. At what time (to the nearest hundreth) is its velocity equal to 384?

Start by finding the velocity function:

v(t) = s'(t) = 12t2 – 6t + 2

To find the time, set v(t) equal to 384: 384 = 12t2 – 6t + 2

To solve, set equal the equation equal to 0: 12t2 – 6t – 382 = 0

Use the quadratic formula:

(–(–6) ± √(36 – 412(–382)))/(2 * 12)

= (6 ± √(36 + 18336))/24 = (6 ± √(18372))/24 = (6 ± 2√(4593))/24

= (3 ± √(4593))/12

Compare your answer with the correct one above

Question

The initial position of a particle is 44.5. If its velocity is described by v(t) = 3t + 12, what is its position at the time when the velocity is equal to 8391?

Answer

The initial position of a particle is 44.5. If its velocity is described by v(t) = 3t + 12, what is its position (to the nearest hundreth) at the time when the velocity is equal to 8391?

To solve for t, set v(t) equal to 8391: 3t + 12 = 8391; 3t = 8379; t = 2793

Now, the position function is equal to ∫v(t)dt = ∫ 3t + 12 dt = (3/2)t2 + 12t + C

Now, since the initial position is 44.5, C is 44.5; therefore, s(t) = (3/2)t2 + 12t + 44.5

To solve for the position, solve s(2793) = (3/2)27932 + 122793 + 44.5 = 1.5 7800849 + 33516 + 44.5 = 11701273.5 + 33516 + 44.5

Compare your answer with the correct one above

Question

The initial position of a particle is 0. If its velocity is described by v(t) = 4t + 5, what is its position at the time when the velocity is equal to 45?

Answer

The position s(t) is equal to ∫v(t) dt = ∫ 4t + 5 dt = 2t2 + 5t + C

Now, since we know that the initial position of the particle (at t = 0) is 0, we know C is 0. Therefore, s(t) = 2t2 + 5t + C

To find the time t when at which the velocity is 45, set v(t) equal to 45. 45 = 4t + 5 → 40 = 4t → t = 10

The position of the particle is s(10) = 2 * 102 + 50 = 200 + 50 = 250

Compare your answer with the correct one above

Question

An eagle flies at a parabolic trajectory such that , where is in the height in meters and is the time in seconds. At what time will its velocity $v=-8 \frac{m}{s}$ ?

Answer

Take the derivative of the position function to obtain the velocity function.

$v(t)=\frac{\mathrm{d} }{\mathrm{d} t}h(t)=-4t$

We want to know the time when the velocity is -8. Substitute v into the equation to find t.

Compare your answer with the correct one above

Question

A ball is thrown in the air, modeled by the function . At what time will the ball hit the ground?

Answer

To find the time when the ball hits the ground, set and solve for .

Separate each term and solve for t.

$t=\frac{3}{2}$

Since negative time does not exist, the only possible answer is $t=\frac{3}{2}$ .

Compare your answer with the correct one above

Question

Suppose the acceleration function of a biker going uphill at the start of a race is , where is in seconds. When will it take the biker to reach constant velocity?

Answer

Constant velocity means there is neither an increase or decrease in acceleration.

Substitute acceleration and solve for time.

Compare your answer with the correct one above

Question

Assume the acceleration due to gravity is

If you throw a ball straight up with an initial velocity of how many seconds will it take before the ball returns to your hand?

Answer

Write out the equation for the height of the ball

$h=-\frac{9.8}{2}t^{2}+9.8t$ .

You can arrive at this by starting with the information that the acceleration on the ball is the constant acceleration due to gravity and integrating twice. Making sure to solve for your constants along the way.

$v(t)=\int a(t)dt = \int -9.8 dt = -9.8t+v_{0}$

$x(t)=\int v(t)dt =\int -9.8t+v_{0}dt=-\frac{9.8}{2}t^{2}+v_{0}t+x_{0}$

Your initial velocity of and your initial position of will help write out this equation.

$x(t)=-\frac{9.8}{2}t^2+9.8t+0$

Then solve for the two values of for which the ball is at height . Those are seconds and seconds.

$\x(t)=-\frac{9.8}{2}t^2+9.8t+0=0\ \ -4.9t^{2}+9.8t=0\ \ t(-4.9t+9.8)=0\ \t=0,t=2$

Compare your answer with the correct one above

Question

A ball is thrown upwards at a speed of from a building. Assume gravity is .

Which of the following is closest to the time after the initial throw before the ball hits the ground?

Answer

If we approximate gravity as we can simplify into and use the quadratic formula to find the time at which the position of the ball is zero (the ball hits the ground).

$t=\frac{-2\pm \sqrt{(2)^2-4(-1)(20)}}{2(-1)}=1\pm\frac{\sqrt{4+80}}{-2}=1\mp\sqrt{21}$

Compare your answer with the correct one above

Question

For this problem, the acceleration of gravity is simplified to $10 \frac{m}{s^2}$ .

I fire a cannon straight into the air. Assuming that the cannonball leaves the cannon at a velocity of $100 \frac{m}{s}$ , weighs kgs, and is fired from the ground (i.e. m), how long will it take before the cannonball reaches the ground again?

Answer

Initial velocity is given as 100 m/s and the acceleration due to gravity is $10\frac{m}{s^2}$ towards the Earth , or $-10 \frac{m}{s^2}$ .

We want to find how long it will take for the velocity of the cannonball to reach , so we set $v = 100 + a\cdot t = 0$ , where t is time and $a = -10 \frac{m}{s^2}$ .

So, , , .

Therefore, it takes ten seconds for the ball to reach a velocity of 0, and given that acceleration is uniform (i.e. a constant), we know that it will take the same amount of time to come down as it took to go up, or ten seconds. Therefore, the total time the cannonball spends in the air is,

seconds.

Compare your answer with the correct one above

Question

Given the instantaneous velocity and the position function, find the time at which the moving object reaches that instantaneous velocity.

Answer

We begin by finding the derivative of the position function using the power rule:

$f(x)=x^n \rightarrow f'(x)=nx^{n-1}$

We then set the given instantaneous velocity equal to the velocity function and solve for t:

$24t+29=125\Rightarrow t=4$

Compare your answer with the correct one above

Question

At what time will a particle whose position can be described by have minimum acceleration?

Answer

We need to take the derivative of acceleration and set it equal to zero because we want to minimize acceleration. In total, this will be three derivatives

$\small x(t)\rightarrow v(t) \rightarrow a(t)\rightarrow \frac{\mathrm{d} }{\mathrm{d} t}a(t)$ .

Using the power rule on each term which states to multiply the coefficient by the exponent then decrease the exponent by one we get the following derivatives.

This will give us

, which gives us $\small t=.27$ and $\small t=-.27$ . Now let's use the second derivative test to see where our minimum is. $\small 480t$ is our second derivative, which is positive at $\small t=.27$ and negative at $\small t=-.27$ , so $\small t=.27$ is our minimum.

Compare your answer with the correct one above

Question

A perfectly spherical hot air balloon is being filled up. If the balloon is empty at the start and has a radius of 50 meters when fully inflated, how fast is the volume of the balloon increasing when its radius is 10 meters and increasing at a rate of $1\frac{m}{min}$ ?

Answer

In order to solve this problem, we must first know that the volume of a sphere is equivalent to $\frac{4}{3}\pi r^3$ .

In order to find the rate of which the volume of this spherical hot air balloon is increasing at, we must take the derivative of the volume equation with respect to time in order to find the change in volume with respect to time.

Using the power rule

$\frac{d}{dt}x^n=nx^{n-1}$ ,

we find that the dervative is

$\frac{dV}{dt}=4\pi r^2\frac{dr}{dt}$ .

In the problem we are given the radius and rate of change of the radius, therefore by plugging those into the equation and solving for $\frac{dV}{dt}$ , we can find the rate at which the volume of the balloon is changing at.

Plugging and $\frac{dr}{dt}=1$ , we find that the volume of the baloon is increasing at a rate of $400 \pi \frac{m}{min}$ .

Compare your answer with the correct one above

Question

Car A starts driving north from point O with an acceleration of . After 2 hours, Car B start driving north from point O with an acceleration of . How long will it take for Car B to catch up with Car A?

Answer

We know that car A's acceleration formula is $a_{A}(t)=10$ and we know that car B's acceleration formula is $a_{B}(t)=30$ . To solve this equation we must realize that the integral of acceleration is velocity and the integral of velocity is position. Therefore by taking the double integral of both acceleration functions, we can determine the point at which car B will catch up to car A.

Using the general integral formula,

$\int x^n=\frac{x^{n+1}}{n+1}+C$

we find that the velocity functions for both cars are $v_{A}(t)=10t$ and $v_{B}(t)=30t$ . Because the initial velocity of both cars is 0, .

Taking the integral of the velocity function using the generla integral formula once again, we find that the position functions of both cars is $S_{A}(t)=5t^2$ and $S_{B}(t)=15t^2$ . Since the initial position of both cars is equivalent, we can arbitrarily say that they start from a initial position 0, therefore making . We know that car A had a head start of 2 hours on car B. Now all we have to do is set both equations equal to each other and solve for .

$t=1+\sqrt{3} hours$

Compare your answer with the correct one above

Question

The position of a particle as a function of time is .

At what time is the particle at rest?

Answer

The particle is at rest when its velocity, i.e. the derivative of its position, is equal to 0.

Thus, we have to solve the equation

.

Using the Power Rule,

.

Thus, either or , leading to the solutions and .

Note: The Power Rule says that for a function

, $p'(x)=knx^{n-1}$ .

Compare your answer with the correct one above

Question

Given the position function, at what time is the velocity going to be equal to zero?

Answer

Velocity is the derivative of position. The derivative of is $nx^{n-1}$ .

Using this information we can find te velocity function.

To find where the velocity is 0, we msut set the velocity function to 0 and factor to solve.

Compare your answer with the correct one above

Question

How much time does it take for a biker accelerating $5 \frac{m}{s^2}$ with initial velocity of $15 \frac{m}{s}$ , and initial position at to travel ?

Answer

First, recall that

$v(t)=\left[\int a(t)dt\right] +v_o$ ,

where is the initial velocity, is the acceleration function, and is velocity.

By the power rule, we know that

$\int at^n dt= \frac{a}{n+1}t^{(n+1)} +C$ ,

where are constants and 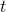is a variable.

In our case,

$v(t)=\left[\int 5dt\right]+15=5t+15$

Also recall that position is given as

$p(t)=\left[\int v(t)dt \right]+p_o$ ,

where is position at any given time and is the initial position.

In our case, where

$p(t)=\int [5t+15]dt= 2.5t^2+15t$ .

To travel , we set up the equation

.

This is equal to

To solve this we use the quadratic formula, which states that for any quadratic equation:

, where are constants, and is a variable

$x=\frac{-B+\sqrt{(B^2-4AC)}}{2A}$

Using the quadratic formula to solve ,

$t=\frac{-6+\sqrt{(6^2-(-4800))}}{21}= \frac{-6+\sqrt{3236}}{2}s$

Compare your answer with the correct one above

Question

A particle is accelerating at a rate given by the expression , where t is the time in seconds after the particle passes a gate inside of the particle accelerator. Two seconds after passing the gate, a radar detects that the particle was moving at a velocity of 50 m/s. The particle will continue to accelerate until it hits a lead wall found approximately 7,000 meters after passing the gate.

Find an expression in terms of t that gives the amount of time in seconds it takes for the particle to reach the wall after passing the gate.

Answer

The acceleration of the particle is given by the follwoing formula: . In order to find the velocity of the particle, this need to be indefinetely integrated.

$v(t)=\int a(t)dt=\int (6t^2+3t+8)dt$

When taking an integral, you can seperate the integral into the sum of the integral of each part.

$\int(6t^2+3t+8)dt= \int6t^2dt+\int3tdt+\int8dt+C$

$\rightarrow \int6t^2dt=\frac{6}{3}t^3$

$\rightarrow\int 3tdt=\frac{3}{2}t^2$

$\rightarrow\int 8dt=8t$

Therefore, the expression for the velocity of the particle is determined to be:

.

In order to find the constant C, you must use the conditions provided to you. The radar detects the velocity of the particle to be equal to 50 m/s two seconds after the particle passes the gate. Use this information to find the constant C.

$2t^3+1.5t^2+8t+C\rightarrow 2(2)^3+1.5(2)^2+8(2)+C= 50$

$\rightarrow16+6+16+C=50$

$\rightarrow C=12$

Now that the expression for velocity has been determined, the position function can be found by integrating the velocity function. The position function is used to find how long it takes for the particle to travel 7000 meters.

$p(t)=\int v(t)dt=\int (2t^3+1.5t^2+8t+12)dt$

Once again, this integral can be seperated into a sum of the integral of each part:

$\int v(t)dt=\int2t^3dt+\int1.5t^2dt+\int 8tdt+\int12dt+C$

$\rightarrow\int2t^3dt=\frac{2}{4}t^4$

$\rightarrow\int\frac{3}{2}t^2dt=\frac{3}{2*3}t^3$

$\rightarrow\int8tdt=\frac{8}{2}t^2$

$\rightarrow\int12dt=12t$

Since the start of the 7000 meters begins at the gate, the initial position of the particle is zero. Therefore, the constant C is equal to zero. This gives a position function for the particle:

By setting this equal to the total distance traveled, the time t that it takes to reach 7000 meters can be determined.

or

Compare your answer with the correct one above

Question

The position of an airplane is described by the function . How long does it take the airplane to travel ?

Answer

We need to find when .

To solve the above equation, use the quadratic equation

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

In this equation, , , , and . Substituting these variables into quadratic equation gives

$t=\frac{12\pm \sqrt{12^{2}-4\cdot3\cdot(-51)}}{2\cdot3}$

$t=\frac{12\pm \sqrt{144+612}}{6}$

$t=\frac{12\pm \sqrt{756}}{6}$

$t=2+\frac{ \sqrt{756}}{6}$ or $t=2-\frac{ \sqrt{756}}{6}$

Since time cannot be negative, the answer is

$t=2+\frac{ \sqrt{756}}{6}$

Compare your answer with the correct one above

Question

The position of a person running is described by the function $r(t)=\frac{1}{2}t^2+t+6$ . How long does it take the person to run miles?

Answer

$r(t)=\frac{1}{2}t^2+t+6$

We need to find when miles.

$10=\frac{1}{2}t^2+t+6$

$0=\frac{1}{2}t^2+t+6-10$

$0=\frac{1}{2}t^2+t-4$

To solve the above equation, use the quadratic equation

$x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}$

In this equation, , , , and . Substituting these variables into quadratic equation gives

$t=\frac{-1\pm \sqrt{1^{2}-4\cdot(1/2)\cdot(-4)}}{2\cdot(1/2)}$

$t=\frac{-1\pm \sqrt{1+8}}{1}$

$t=\frac{-1\pm \sqrt{9}}{1}$

or

Time cannot be negative, so the answer is

Compare your answer with the correct one above

Question

The velocity of a rocket shot into the air is described by the function . How long does it take the rocket to reach its highest point?

Answer

The rocket has reached it's highest point when . Substituting this into the equation gives

Solving for , gives

$t=\frac{100}{9.8}=10.2$

Compare your answer with the correct one above

Tap the card to reveal the answer