Increasing Intervals - CLEP Calculus
Card 0 of 20
On what intervals does f(x) = (1/3)x3 + 2.5x2 – 14x + 25 increase?
On what intervals does f(x) = (1/3)x3 + 2.5x2 – 14x + 25 increase?
We will use the tangent line slope to ascertain the increasing / decreasing of f(x). To this end, let us begin by taking the first derivative of f(x):
f'(x) = x2 + 5x – 14
Solve for the potential relative maxima and minima by setting f'(x) to 0 and solving:
x2 + 5x – 14 = 0; (x – 2)(x + 7) = 0
Potential relative maxima / minima: x = 2, x = –7
We must test the following intervals: (–∞, –7), (–7, 2), (2, ∞)
f'(–10) = 100 – 50 – 14 = 36
f'(0) = –14
f'(10) = 100 + 50 – 14 = 136
Therefore, the equation increases on (–∞, –7) and (2, ∞)
We will use the tangent line slope to ascertain the increasing / decreasing of f(x). To this end, let us begin by taking the first derivative of f(x):
f'(x) = x2 + 5x – 14
Solve for the potential relative maxima and minima by setting f'(x) to 0 and solving:
x2 + 5x – 14 = 0; (x – 2)(x + 7) = 0
Potential relative maxima / minima: x = 2, x = –7
We must test the following intervals: (–∞, –7), (–7, 2), (2, ∞)
f'(–10) = 100 – 50 – 14 = 36
f'(0) = –14
f'(10) = 100 + 50 – 14 = 136
Therefore, the equation increases on (–∞, –7) and (2, ∞)
Compare your answer with the correct one above
Find the interval(s) where the following function is increasing. Graph to double check your answer.

Find the interval(s) where the following function is increasing. Graph to double check your answer.
To find when a function is increasing, you must first take the derivative, then set it equal to 0, and then find between which zero values the function is positive.
First, take the derivative:

Set equal to 0 and solve:



Now test values on all sides of these to find when the function is positive, and therefore increasing. I will test the values of -6, 0, and 2.




Since the values that are positive is when x=-6 and 2, the interval is increasing on the intervals that include these values. Therefore, our answer is:

To find when a function is increasing, you must first take the derivative, then set it equal to 0, and then find between which zero values the function is positive.
First, take the derivative:
Set equal to 0 and solve:
Now test values on all sides of these to find when the function is positive, and therefore increasing. I will test the values of -6, 0, and 2.
Since the values that are positive is when x=-6 and 2, the interval is increasing on the intervals that include these values. Therefore, our answer is:
Compare your answer with the correct one above
Find the interval(s) where the following function is increasing. Graph to double check your answer.

Find the interval(s) where the following function is increasing. Graph to double check your answer.
To find when a function is increasing, you must first take the derivative, then set it equal to 0, and then find between which zero values the function is positive.
First, take the derivative:

Set equal to 0 and solve:



Now test values on all sides of these to find when the function is positive, and therefore increasing. I will test the values of 0, 2, and 10.




Since the value that is positive is when x=0 and 10, the interval is increasing in both of those intervals. Therefore, our answer is:

To find when a function is increasing, you must first take the derivative, then set it equal to 0, and then find between which zero values the function is positive.
First, take the derivative:
Set equal to 0 and solve:
Now test values on all sides of these to find when the function is positive, and therefore increasing. I will test the values of 0, 2, and 10.
Since the value that is positive is when x=0 and 10, the interval is increasing in both of those intervals. Therefore, our answer is:
Compare your answer with the correct one above
Is  increasing or decreasing on the interval
increasing or decreasing on the interval  ?
?

Is 

To find increasing and decreasing intervals, we need to find where our first derivative is greater than or less than zero. If our first derivative is positive, our original function is increasing and if g'(x) is negative, g(x) is decreasing.
Begin with:



If we plug in any number from 3 to 6, we get a positve number for g'(x), So, this function must be increasing on the interval {3,6}, because g'(x) is positive.
To find increasing and decreasing intervals, we need to find where our first derivative is greater than or less than zero. If our first derivative is positive, our original function is increasing and if g'(x) is negative, g(x) is decreasing.
Begin with:
If we plug in any number from 3 to 6, we get a positve number for g'(x), So, this function must be increasing on the interval {3,6}, because g'(x) is positive.
Compare your answer with the correct one above
Is  increasing or decreasing on the interval
increasing or decreasing on the interval ![[-5,-8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/325742/gif.latex) ?
?

Is 
![[-5,-8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/325742/gif.latex)
To find out if a function is increasing or decreasing, we need to find if the first derivative is positive or negative on the given interval.
So starting with:

We get:
 using the Power Rule
using the Power Rule  .
.
Find the function on each end of the interval.


So the first derivative is positive on the whole interval, thus g(t) is increasing on the interval.
To find out if a function is increasing or decreasing, we need to find if the first derivative is positive or negative on the given interval.
So starting with:
We get:


Find the function on each end of the interval.
So the first derivative is positive on the whole interval, thus g(t) is increasing on the interval.
Compare your answer with the correct one above
Is the following function increasing or decreasing on the interval ![[2,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/325776/gif.latex) ?
?

Is the following function increasing or decreasing on the interval ![[2,3]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/325776/gif.latex)
A function is increasing on an interval if for every point on that interval the first derivative is positive.
So we need to find the first derivative and then plug in the endpoints of our interval.

Find the first derivative by using the Power Rule 

Plug in the endpoints and evaluate the function.


Both are positive, so our function is increasing on the given interval.
A function is increasing on an interval if for every point on that interval the first derivative is positive.
So we need to find the first derivative and then plug in the endpoints of our interval.
Find the first derivative by using the Power Rule
Plug in the endpoints and evaluate the function.
Both are positive, so our function is increasing on the given interval.
Compare your answer with the correct one above
On which intervals is the following function increasing?

On which intervals is the following function increasing?
The first step is to find the first derivative.

Remember that the derivative of 
Next, find the critical points, which are the points where  or undefined. To find the
or undefined. To find the  points, set the numerator to
points, set the numerator to  , to find the undefined points, set the denomintor to
, to find the undefined points, set the denomintor to  . The critical points are
. The critical points are  and
and 
The final step is to try points in all the regions  to see which range gives a positive value for
to see which range gives a positive value for  .
.
If we plugin in a number from the first range, i.e  , we get a negative number.
, we get a negative number.
From the second range,  , we get a positive number.
, we get a positive number.
From the third range,  , we get a negative number.
, we get a negative number.
From the last range,  , we get a positive number.
, we get a positive number.
So the second and the last ranges are the ones where  is increasing.
is increasing.
The first step is to find the first derivative.
Remember that the derivative of
Next, find the critical points, which are the points where 




The final step is to try points in all the regions 

If we plugin in a number from the first range, i.e 
From the second range, 
From the third range, 
From the last range, 
So the second and the last ranges are the ones where 
Compare your answer with the correct one above
Below is the complete graph of  . On what interval(s) is
. On what interval(s) is  increasing?
increasing?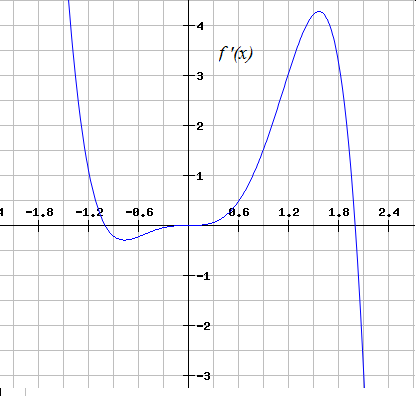
Below is the complete graph of 


 is increasing when
is increasing when  is positive (above the
is positive (above the  -axis). This occurs on the intervals
-axis). This occurs on the intervals  .
.




Compare your answer with the correct one above
Function A

Function B

Function C

**Function D

Function E

5 graphs of different functions are shown above. Which graph shows an increasing/non-decreasing function?
Function A
Function B
Function C
**Function D
Function E
5 graphs of different functions are shown above. Which graph shows an increasing/non-decreasing function?
A function  is increasing if, for any
is increasing if, for any  ,
,  (i.e the slope is always greater than or equal to zero)
(i.e the slope is always greater than or equal to zero)
Function E is the only function that has this property. Note that function E is increasing, but not strictly increasing
A function 


Function E is the only function that has this property. Note that function E is increasing, but not strictly increasing
Compare your answer with the correct one above
Find the increasing intervals of the following function on the interval  :
:

Find the increasing intervals of the following function on the interval 
To find the increasing intervals of a given function, one must determine the intervals where the function has a positive first derivative. To find these intervals, first find the critical values, or the points at which the first derivative of the function is equal to zero.
For the given function,  .
.
This derivative was found by using the power rule
 .
.
When set equal to zero,  . Because we are only considering the open interval (0,5) for this function, we can ignore
. Because we are only considering the open interval (0,5) for this function, we can ignore  . Next, we look the intervals around the critical value
. Next, we look the intervals around the critical value  , which are
, which are  and
and  . On the first interval, the first derivative of the function is negative (plugging in values gives us a negative number), which means that the function is decreasing on this interval. However for the second interval, the first derivative is positive, which indicates that the function is increasing on this interval
. On the first interval, the first derivative of the function is negative (plugging in values gives us a negative number), which means that the function is decreasing on this interval. However for the second interval, the first derivative is positive, which indicates that the function is increasing on this interval  .
.
To find the increasing intervals of a given function, one must determine the intervals where the function has a positive first derivative. To find these intervals, first find the critical values, or the points at which the first derivative of the function is equal to zero.
For the given function, 
This derivative was found by using the power rule

When set equal to zero, 





Compare your answer with the correct one above
Is  increasing, decreasing, or flat at
increasing, decreasing, or flat at  ?
?

Is 

Is f(x) increasing, decreasing, or flat at  ?
?

Recall that to find if a function is increasing or decreasing, we can use its first derivative. If f'(x) is positive, f(x) is increasing. If f'(x) is negative, f(x) is decreasing.
So, given:

We get

Then:

Therefore, f(x) is decreasing at the point, because f'(x) is negative.
Is f(x) increasing, decreasing, or flat at 
Recall that to find if a function is increasing or decreasing, we can use its first derivative. If f'(x) is positive, f(x) is increasing. If f'(x) is negative, f(x) is decreasing.
So, given:
We get
Then:
Therefore, f(x) is decreasing at the point, because f'(x) is negative.
Compare your answer with the correct one above
Tell whether  is increasing or decreasing on the interval
is increasing or decreasing on the interval ![[4,7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/384983/gif.latex) .
.

Tell whether 
![[4,7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/384983/gif.latex)
Tell whether g(t) is increasing or decreasing on the interval \[4,7\]

To find increasing and decreasing, find where the first derivative is positive and negative. If g'(t) is positive, then g(t) is increasing and vice-versa.


Then,plug in the endpoints of \[4,7\] and see what you get for a sign.


So, since g'(t) is positive on the interval, g(t) is increasing.
Tell whether g(t) is increasing or decreasing on the interval \[4,7\]
To find increasing and decreasing, find where the first derivative is positive and negative. If g'(t) is positive, then g(t) is increasing and vice-versa.
Then,plug in the endpoints of \[4,7\] and see what you get for a sign.
So, since g'(t) is positive on the interval, g(t) is increasing.
Compare your answer with the correct one above
Find the interval on which the function is increasing:

Find the interval on which the function is increasing:
To find the interval(s) on which the function is increasing, we must find the intervals on which the first derivative of the function is positive.
The first derivative of the function is:

and was found using the rule

Now we must find the critical value, at which the first derivative is equal to zero:

Now, we make the intervals on which we look at the sign of the first derivative:

On the first interval the first derivative is positive, while on the second it is negative. Thus, the first interval is our answer, because over this range of x values, the first derivative is positive and the function is increasing.
To find the interval(s) on which the function is increasing, we must find the intervals on which the first derivative of the function is positive.
The first derivative of the function is:
and was found using the rule
Now we must find the critical value, at which the first derivative is equal to zero:
Now, we make the intervals on which we look at the sign of the first derivative:
On the first interval the first derivative is positive, while on the second it is negative. Thus, the first interval is our answer, because over this range of x values, the first derivative is positive and the function is increasing.
Compare your answer with the correct one above
Deletable Note to the admin: I am virtually 100% sure the derivative has been correct. Derivative of the top is 6x. Derivative of the bottom is 1/x. So numerator of derivative by quotient rule is  . You will note the second term in this is 3x. Denominator is self explanatory. I do not see where it is wrong.
. You will note the second term in this is 3x. Denominator is self explanatory. I do not see where it is wrong.
Let  . On what subintervals of the interval
. On what subintervals of the interval  is
is  increasing?
increasing?
Deletable Note to the admin: I am virtually 100% sure the derivative has been correct. Derivative of the top is 6x. Derivative of the bottom is 1/x. So numerator of derivative by quotient rule is 
Let 


Take the first derivative of  :
:
 by quotient rule
by quotient rule
 is increasing whenever
is increasing whenever  is positive, that is, whenever both the numerator and denominator are of the same sign. The function
is positive, that is, whenever both the numerator and denominator are of the same sign. The function  is certainly positive for all values of
is certainly positive for all values of  greater than
greater than  because and since
because and since

is positive for all positive  , it is increasing on the interval, too. It will never be negative. For the same reason, the numerator is always positive. With the numerator and denominator always positive everywhere on the given interval, the derivative is always positive and the function is always increasing. So for any interval of nonzero length within
, it is increasing on the interval, too. It will never be negative. For the same reason, the numerator is always positive. With the numerator and denominator always positive everywhere on the given interval, the derivative is always positive and the function is always increasing. So for any interval of nonzero length within  ,
,  is increasing.
is increasing.
NOTE: Interestingly the opposite of the choice  >
>  is also true.
is also true.  on the entire interval because at
on the entire interval because at  , we have
, we have
 . So the numerator is larger to begin with, and since:
. So the numerator is larger to begin with, and since:
 for all
for all  (or any
(or any  for that matter), the derivative of the numerator is greater, too. This means the numerator will always be larger, so this condition coincides with the condition of
for that matter), the derivative of the numerator is greater, too. This means the numerator will always be larger, so this condition coincides with the condition of  being positive.
being positive.
Take the first derivative of 






is positive for all positive 


NOTE: Interestingly the opposite of the choice 








Compare your answer with the correct one above
Suppose  is continuous for all
is continuous for all  and known to have at least one root, and
and known to have at least one root, and  for all
for all  . Which of the following must be true?
. Which of the following must be true?
Suppose 



If  is continuous everywhere and always increasing (i.e.
is continuous everywhere and always increasing (i.e.  for all
for all  ), then it must be true that after
), then it must be true that after  has attained its root, it can never do so again because it can't "return" to the
has attained its root, it can never do so again because it can't "return" to the  -axis. NOTE: this is not automatically true of functions that aren't continuous. As for the other choices, the possibility of at least having one more root is automatically false and a simple counterexample to the notion thay
-axis. NOTE: this is not automatically true of functions that aren't continuous. As for the other choices, the possibility of at least having one more root is automatically false and a simple counterexample to the notion thay  has to have an inflection point is a simple increasing lines. It has a constant positive derivative, but possesses no upward or downward concavity and has no inflection points.
has to have an inflection point is a simple increasing lines. It has a constant positive derivative, but possesses no upward or downward concavity and has no inflection points.
If 





Compare your answer with the correct one above
Find the intervals on which the following function is increasing:

Find the intervals on which the following function is increasing:
To find the intervals on which the function is increasing, we must find the intervals where the first derivative is positive. To do this, we must find the first derivative, and find its critical values (at which the first derivative is equal to zero):


The derivative was found using the following rule:

Now, write the intervals of the function for which c is the upper and lower bound:

Note that at the critical value, the derivative is neither positive nor negative.
Now, we analyze the sign of the derivative within each interval; on the first interval, the derivative is always negative, but on the second interval, the first derivative is always positive. In other words, for this set of values -  - the function is increasing.
- the function is increasing.
To find the intervals on which the function is increasing, we must find the intervals where the first derivative is positive. To do this, we must find the first derivative, and find its critical values (at which the first derivative is equal to zero):
The derivative was found using the following rule:
Now, write the intervals of the function for which c is the upper and lower bound:
Note that at the critical value, the derivative is neither positive nor negative.
Now, we analyze the sign of the derivative within each interval; on the first interval, the derivative is always negative, but on the second interval, the first derivative is always positive. In other words, for this set of values - 
Compare your answer with the correct one above
Determint the intervals on which the following function is increasing:

Determint the intervals on which the following function is increasing:
To determine the intervals on which the function is increasing, we must determine the intervals on which the first derivative of the function is positive. To start, we must find the first derivative:

The derivative was found using the following rule:

The first derivative is a positive constant, therefore the function is increasing on the entire domain,  .
.
To determine the intervals on which the function is increasing, we must determine the intervals on which the first derivative of the function is positive. To start, we must find the first derivative:
The derivative was found using the following rule:
The first derivative is a positive constant, therefore the function is increasing on the entire domain, 
Compare your answer with the correct one above
When is the function  increasing?
increasing?
When is the function 
To find where the function is increasing, you must first find the derivative of the function so you can test critical points. The derivative of the function is  . Then, set that equal to
. Then, set that equal to  to find the critical points. When you set that equal to
to find the critical points. When you set that equal to  , you get
, you get  . Then set up a number line so you can test values to determine when the function is increasing and decreasing. We know it's changing direction at our critical point,
. Then set up a number line so you can test values to determine when the function is increasing and decreasing. We know it's changing direction at our critical point,  . So let's pick a point to the left of
. So let's pick a point to the left of  and plug it in to the derivative. I'll pick
and plug it in to the derivative. I'll pick  :
:  . Since the answer is negative, we know that the function is decreasing. Pick a point to the right of 2. I'll pick 3:
. Since the answer is negative, we know that the function is decreasing. Pick a point to the right of 2. I'll pick 3:  . Since the answer is positive, the function is increasing. Therefore, the function is increasing from
. Since the answer is positive, the function is increasing. Therefore, the function is increasing from  .
.
To find where the function is increasing, you must first find the derivative of the function so you can test critical points. The derivative of the function is 









Compare your answer with the correct one above
Find the intervals on which the function is increasing:

Find the intervals on which the function is increasing:
To find the intervals on which the function is increasing, we must find the intervals on which the first derivative is positive.
To start, we must first find where the first derivative of the function is zero:

The first derivative was found using the following rule:

Now, set this function equal to zero to get the critical values (values at which the first derivative is equal to zero):

Next, we create the intervals using the critical value as the upper and lower bound of the limits, respectively:

On the first interval, the first derivative is negative, but on the second interval, the first derivative is positive, meaning that on this interval the function is increasing. (Simply plug in any point on the interval into the first derivative function and check the sign.)
The answer is 
To find the intervals on which the function is increasing, we must find the intervals on which the first derivative is positive.
To start, we must first find where the first derivative of the function is zero:
The first derivative was found using the following rule:
Now, set this function equal to zero to get the critical values (values at which the first derivative is equal to zero):
Next, we create the intervals using the critical value as the upper and lower bound of the limits, respectively:
On the first interval, the first derivative is negative, but on the second interval, the first derivative is positive, meaning that on this interval the function is increasing. (Simply plug in any point on the interval into the first derivative function and check the sign.)
The answer is
Compare your answer with the correct one above
Find the interval on which the following function is increasing.

Find the interval on which the following function is increasing.
To solve, you must first differentiate the function once and then find where the derivative is positive. To differentiate, use the power rule:

Thus,

Now you must find where this is greater than 0, and therefore increasing.



Therefore, our answer is when x is greater than 2. Thus,  .
.
To solve, you must first differentiate the function once and then find where the derivative is positive. To differentiate, use the power rule:
Thus,
Now you must find where this is greater than 0, and therefore increasing.
Therefore, our answer is when x is greater than 2. Thus, 
Compare your answer with the correct one above