Equations - CLEP Calculus

Card 0 of 20

Question

Determine given that .

Answer

This problem requires you to evaluate an indefinite integral of the given function f’(x). Integrating each term of the function with respect to x, we simply divide each coefficient by (n+1), where n is the value of the exponent on x for that particular term, and then add 1 to the value of the exponent on each x. This gives us:

$f(x)=\int f'(x)dx=\int (15x^4+14x^3-9x^2+5x-16)dx$

$f(x)=3x^5+\frac{7}{2}x^4-3x^3+\frac{5}{2}x^2-16x+C$

A correct answer must include a constant C, as the original function may have had a constant that is not reflected in the equation for its derivative.

Compare your answer with the correct one above

Question

What is the area under the curve for ?

Answer

By normal exponent rules $2^x = e^{x \ln 2}$ , and so we set up the definite integral

$\int_{-\infty}^{0} e^{x \ln 2} ~dx$ ,

which integrates to:

$\left[ \frac{e^{x \ln 2}}{\ln 2}\right]_{-\infty}^0 = \frac{2^0 - 2^{-\infty}}{\ln 2} = \frac{1 - 0}{\ln 2}$

Compare your answer with the correct one above

Question

The Gaussian integral formula states that

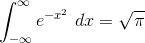$\int_{-\infty}^{\infty} e^{-x^2} ~ dx = \sqrt{\pi}$ .

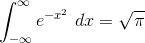
What is the integral of

$\int_{-\infty}^{\infty} x^2 ~ e^{-x^2} ~ dx$ ?

Answer

Integrating by parts with

,

$v = - \frac{1}{2} e^{-x^2}$ , $dv = x ~e^{-x^2}~dx$ ,

we get:

$\int_{-\infty}^{\infty} x^2 e^{-x^2} dx = \int_A^B u ~ dv = \left[ u v\right ]_A^B - \int_A^B v ~ du$

$= \left[ \frac{-x}{2} e^{-x^2} \right ]_{-\infty}^{\infty} - \int_{-\infty}^{\infty} \frac{-1}{2} e^{-x^2}~ dx = [0 - 0] - \frac{-1}{2} \sqrt{\pi} = \frac{\sqrt{\pi}}{2}$

Compare your answer with the correct one above

Question

What is the value of the following definite integral?

$\int_{0}^{\pi /2}\bigg(-5sin(x)-3cos(x)+\frac{4}{\pi }\bigg)dx$

Answer

We start by integrating the function in parentheses with respect to x, and we then subtract the evaluation of the lower limit from the evaluation of the upper limit:

$\int_{0}^{\pi /2}\bigg(-5sin(x)-3cos(x)+\frac{4}{\pi })dx=(5cos(x)-3sin(x)+\frac{4}{\pi }x\bigg)_{0}^{\pi /2}$

$=(5cos(\frac{\pi }{2})-3sin(\frac{\pi }{2})+\frac{4}{\pi }(\frac{\pi }{2}))-(5cos(0)-3sin(0)+\frac{4}{\pi}(0))$

Compare your answer with the correct one above

Question

Determine the amount of work required to push a box from meters to meters, given the function for force below:

$F(x)=x^2-sin(2x)+\frac{1}{x}$

Answer

This problem intends to demonstrate one possible application of calculus to the field of physics. An equation for work as given in physics is as follows:

$W=\int F(x)dx$

Using this equation, we simply set up a definite integral with our bounds given by the interval of interest in the problem:

$W=\int_{2}^{5}\bigg(x^2-sin(2x)+\frac{1}{x}\bigg)dx$

$W=\bigg(\frac{1}{3}x^3+\frac{1}{2}cos(2x)+ln(x)\bigg)_{2}^{5}$

$W=\bigg(\frac{1}{3}(5)^3+\frac{1}{2}cos(10)+ln(5)\bigg)-\bigg(\frac{1}{3}(2)^3+\frac{1}{2}cos(4)+ln(2)\bigg)$

Joules

After evaluating our integral, we can see that the work required to push the box from x=2 meters to x=5 meters is 39.8 Joules.

Compare your answer with the correct one above

Question

Write out the expression of the area under the following curve from to .

Answer

Simply use an integral expression with the given x values as your bounds.

Don't forget to add the dx!

$\int_{1}^{4}(6x^2+4x+5)dx$

Compare your answer with the correct one above

Question

Evaluate the definite integral within the interval $0\leq x \leq 1$ .

$\int(5x^{4}+x^{2}-x)dx$

Answer

In order to solve this problem we must know that

$\int_{a}^{b}f(x)=F(b)-F(a)$

In this case we have:

$\int_{0}^{1} (5x^{4}+x^{2}-x)dx$

Our first step is to integrate:

$\int(5x^{4}+x^{2}-x) dx=x^{5}+\frac{1}{3}x^{3}-\frac{1}{2}x^{2}$

We then arrive to our solution by plugging in our values

$\left [ (1)^{5}+\frac{1}3{(1)^{3}-\frac{1}{2}(1)^{2}} \right ]-\left [ (0)^{5}+\frac{1}{3}(0)^{3}-\frac{1}{2}(0)^{2} \right ]$

$\left ( 1+\frac{1}{3}-\frac{1}{2} \right )-0=\frac{5}{6}$

Compare your answer with the correct one above

Question

Suppose a student wants to find the area under the curve between functions , , and . Find the correct integral that will determine the area.

Answer

The region bounded by the three functions represents a triangle. It will be easier to determine the bounded region by subtracting the left curve from the right curve, and using to integrate. In order to integrate in terms of , any equation in terms of must be rewritten in terms of .

Isolate .

$x=\frac{y}{2}$

Find the intersection of the lines $x=\frac{y}{2}$ and .

$2=\frac{y}{2}$

The correct bounds are from . Write the correct integral.

$\int_{0}^{4}2-\frac{y}{2}: dy$

Compare your answer with the correct one above

Question

Evaluate the definite integral within the interval $1\leq x \leq 2$ .

$\int (2x^{3}+\frac{1}{2}x^{2}+7)dx$

Answer

In order to solve this problem we must remember that:

$\int_{a}^{b}f(x)=F(b)-F(a)$

In this case we have:

$\int_{1}^{2}(2x^{3}+\frac{1}{2}x^{2}+7) dx$

Our first step is to integrate:

$\int (2x^3+\frac{1}{2}x^2+7)dx= \frac{1}{2}x^4+\frac{1}{6}x^3+7x$

We then arrive at our solution by plugging in our values

$\left[\frac{1}{2}(2)^4+\frac{1}{6}(2)^3+7(2)\right]-\left[\frac{1}{2}(1)^4+\frac{1}{6}(1)^3+7(1)\right]$

$\left ( 8+\frac{4}{3} +14 \right)-\left(\frac{1}{2}+\frac{1}{6}+7 \right)=\frac{47}{3}$

Compare your answer with the correct one above

Question

Evaluate the definite integral within the interval $4\leq x \leq 9$

$\int \left(\frac{1}{\sqrt{x}}+3x^2-4\right)dx$

Answer

In order to solve this problem we must remember that:

$\int_{a}^{b}f(x)=F(b)-F(a)$

In this case we have:

$\int_{4}^{9}\left(\frac{1}{\sqrt{x}}+3x^2-4\right)dx$

Our first step is to integrate:

$\int\left(\frac{1}{\sqrt{x}}+3x^2-4\right)dx=2\sqrt{x}+x^{3}-4x$

We then arrive to our solution by plugging in our values

$\left [ 2\sqrt{9}+(9)^{3}-4(9) \right ]-\left [ 2\sqrt{4}+(4)^{3}-4(4) \right ]$

Compare your answer with the correct one above

Question

Evaluate the indefinite integral.

$\int (5+4x)dx$

Answer

We are being asked to integrate the function.

To do this we need to remember the power rule of integrals,

$\int (a+bx)dx=ax+\frac{bx^n+1}{n+1}+c$

Using this rule, we can evaluate the following integral:

$\int (5+4x)dx = 5x+2x^2+c$

Compare your answer with the correct one above

Question

Evaluate the indefinite integral.

$\int \left(\frac{1}{\sqrt{x}}+5\right)dx$

Answer

In this problem we are being asked to integrate the function.

In order to do this we need to remember,

$\int (x^{-n}+a)dx=\frac{x^{-n+1}}{-n+1}+ax+c$ .

Since

$\frac{1}{\sqrt x}=x^{-1/2} \rightarrow \int x^{-1/2}=\frac{x^{1/2}}{\frac{1}{2}}=2x^{1/2}=2\sqrt x$

then the integral,

$\int \left(\frac{1}{\sqrt{x}}+5\right)dx= 2\sqrt{x}+5x+c$ .

Compare your answer with the correct one above

Question

Evaluate the indefinite integral.

$\int(10x) dx$

Answer

This problem is asking us to integrate the function.

In order to do this we need to remember,

$\int (ax )dx=\frac{ax^{n+1}}{n+1}+c$ .

Therefore,

$\int(10x) dx=5x^2+c$

Compare your answer with the correct one above

Question

Which of the following integrals could be evaluated to find the area under the curve of the following function from 3 to 13?

Answer

We are asked to set up an integral without solving it. We want to evaluate the function from 3 to 13, so 3 goes at the bottom of the integral and 13 goes at the top. No other options have this correct.

Compare your answer with the correct one above

Question

Write an integral expression which will solve the area under the curve of , bounded by , from .

Answer

Recall that area under the curve requires integration from either top minus bottom curve, or right minus left curve.

The top curve is:

The bottom curve is:

The interval indicates that the lower bound is 2 and the upper bound is 5.

Write the integral.

$\int_{2}^{5}(1+x )dx$

Compare your answer with the correct one above

Question

Write the correct expression to find the area of from .

Answer

This is a tricky question.

If we chose $\int_{-2}^{2}xdx$ , the region in the third quadrant of is negative area, since is no longer the top curve. Evaluating this integral will cancel out the negative area in the third quadrant with the positive area on the first quadrant. This integral will give zero area, which is incorrect.

The correct method is to split this interval into 2 separate integrations: One from and the other from .

From interval , the top curve is minus the bottom curve, , is .

From interval , the top curve is minus the bottom curve, , is .

Set up the integral.

$\int_{-2}^{0}-xdx+\int_{0}^{2}xdx$

Compare your answer with the correct one above

Question

Which of the following expressions could be evaluated to find the area under on the interval ?

$f(x)=\sqrt{3x} + 17x^3+5x^2-14$

Answer

To find the area under a curve, we usually want to use an integral. All of our answer choices are integrals though, so this doesn't narrow things down. Then next thing to look for are our limits of integration. In this case, we are on the interval \[360,540\], so look for an option that has the lower limit of integration as 360 and the higher limit as 540. Only one option has this:

$\int_{360}^{540}\sqrt{3x} + 17x^3+5x^2-14dx$

For further clarification, to set up an integral, we want our function within the integral and our limits of integration on the integral sign itself. Once we have the correct integral set up, we can evaluate it to find the area under the curve.

Compare your answer with the correct one above

Question

Evaluate:

$\ \int x^2+x+1$

Answer

We get this by applying the inverse power rule to each polynomial term.

$\int x^n=\frac{x^{n+1}}{n+1}$

Therefore we get,

$\ \int x^2+x+1=\frac{1}{3}x^3+\frac{1}{2}x^2+x+C$

Since this is an indefinite integral, we need to add a constant term at the end of the function.

Compare your answer with the correct one above

Question

Evaluate the following definite integral:

$\int_{0}^{1}3x^2+5$

Answer

There are two steps to evaluating a definite integral. The first step is finding the anti-derivative of the function that we are integrating. In this problem, we are integrating the function , and the anti-derivative of this function is . (To check that your anti-derivative is correct, derive it. If you do not arrive back at the original function, go back and find where you may have made a mistake).

The second step is evaluating the anti-derivative at the given endpoints, and subtracting the second from the first. To do this, we look at the two endpoints, or "limits of integration," and decide which is higher. In this case, the two limits are and , and so we first evaluate the anti-derivative at . So, we get . Next, we evaluate at , and get , and subtracting this from the first value, we get .

Compare your answer with the correct one above

Question

Suppose a function . Setup an integral that will evaluate the area under the curve if this parabola is bounded by .

Answer

First, in order to find the zeros of the function, we need to use the quadratic formula.

$\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

In our case,

.

$\frac{-8\pm \sqrt{8^2-4(-1)(-9)}}{2(-1)}$

$\frac{-8\pm\sqrt{28}}{-2}=1.35, 6.65$

These will be the lower and upper bounds of the integral.

Set up the integral in terms of .

$\int_{1.35}^{6.65}-x^2+8x-9:dx$

Compare your answer with the correct one above

Tap the card to reveal the answer