Functions - CLEP Calculus
Card 0 of 20
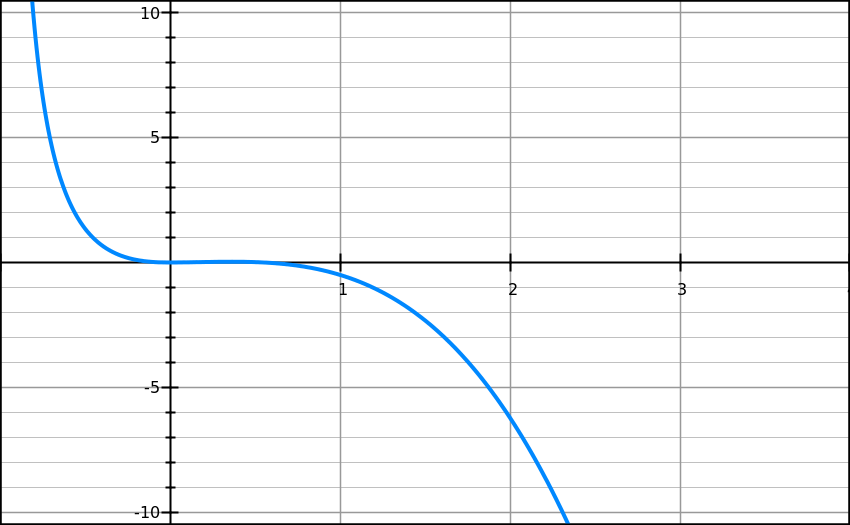
Suppose a point on the curve given above has the property that  .
.
Based solely on the graph above, which of the following is most likely the 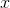 value of the point in question?
value of the point in question?

Suppose a point on the curve given above has the property that 
Based solely on the graph above, which of the following is most likely the 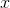
If then the graph must be concave up at the point. Based on the picture, we know that the curve is concave up on
then the graph must be concave up at the point. Based on the picture, we know that the curve is concave up on 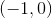 at best. The only value that falls on this interval is
at best. The only value that falls on this interval is  , which is
, which is 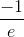 . Since
. Since  , this definitely falls on the interval given and we can be sure it is concave up based on the picture.
, this definitely falls on the interval given and we can be sure it is concave up based on the picture.
If


Compare your answer with the correct one above
What is the critical point for  ?
?
What is the critical point for 
To find the critical point, you must find the derivative first. To do that, multiply the exponent by the coefficient in front of the  and then subtract the exponent by
and then subtract the exponent by  . Therefore, the derivative is:
. Therefore, the derivative is:  . Then, to find the critical point, set the derivative equal to
. Then, to find the critical point, set the derivative equal to  .
.
 .
.
To find the critical point, you must find the derivative first. To do that, multiply the exponent by the coefficient in front of the 




Compare your answer with the correct one above

Suppose a point on the curve given above has the property that  .
.
Based solely on the graph above, which of the following is most likely the 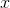 value of the point in question?
value of the point in question?

Suppose a point on the curve given above has the property that 
Based solely on the graph above, which of the following is most likely the 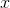
If then the graph must be concave up at the point. Based on the picture, we know that the curve is concave up on
then the graph must be concave up at the point. Based on the picture, we know that the curve is concave up on 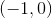 at best. The only value that falls on this interval is
at best. The only value that falls on this interval is  , which is
, which is 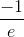 . Since
. Since  , this definitely falls on the interval given and we can be sure it is concave up based on the picture.
, this definitely falls on the interval given and we can be sure it is concave up based on the picture.
If
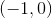

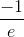

Compare your answer with the correct one above
What is the critical point for  ?
?
What is the critical point for 
To find the critical point, you must find the derivative first. To do that, multiply the exponent by the coefficient in front of the  and then subtract the exponent by
and then subtract the exponent by  . Therefore, the derivative is:
. Therefore, the derivative is:  . Then, to find the critical point, set the derivative equal to
. Then, to find the critical point, set the derivative equal to  .
.
 .
.
To find the critical point, you must find the derivative first. To do that, multiply the exponent by the coefficient in front of the 




Compare your answer with the correct one above
Find the average rate of change for  over the interval
over the interval ![x=[0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/448743/gif.latex) .
.
Find the average rate of change for 
![x=[0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/448743/gif.latex)
The rate of change of a function is the amount it changes over a given amount of time.
In mathematical terms, this can be written as

we plug in our values:

Note that this is only an average because quadratic functions change at different rates depending on where you are in the function's domain.
The rate of change of a function is the amount it changes over a given amount of time.
In mathematical terms, this can be written as
we plug in our values:
Note that this is only an average because quadratic functions change at different rates depending on where you are in the function's domain.
Compare your answer with the correct one above
Let  . Use linear approximation to estimate
. Use linear approximation to estimate  .
.
Let 

Note that:

Therefore, for values relatively close to 1, we can use the formula for dy (the differential form of the derivative) to estimate f at close values.
 From log derivative with chain rule.
From log derivative with chain rule.
Since  lies
lies  to the right of
to the right of  ,
,  and
and  for the estimation, so:
for the estimation, so:

So then:

Note that:
Therefore, for values relatively close to 1, we can use the formula for dy (the differential form of the derivative) to estimate f at close values.

Since 




So then:
Compare your answer with the correct one above
Using  , approximate the value of
, approximate the value of 
Using 
First, we need to rearrange the given to match the approximation formula.  Therefore,
Therefore, 
First, we need to rearrange the given to match the approximation formula. 
Compare your answer with the correct one above
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length  ?
?
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length 
Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:

The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:

Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:



Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:
The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:
Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:
Compare your answer with the correct one above
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length  ?
?
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length 
Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:

The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:

Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:



Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:
The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:
Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:
Compare your answer with the correct one above
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length  ?
?
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length 
Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:

The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:

Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:



Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:
The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:
Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:
Compare your answer with the correct one above
Find the average rate of change for  over the interval
over the interval ![x=[0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/448743/gif.latex) .
.
Find the average rate of change for 
![x=[0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/448743/gif.latex)
The rate of change of a function is the amount it changes over a given amount of time.
In mathematical terms, this can be written as

we plug in our values:

Note that this is only an average because quadratic functions change at different rates depending on where you are in the function's domain.
The rate of change of a function is the amount it changes over a given amount of time.
In mathematical terms, this can be written as
we plug in our values:
Note that this is only an average because quadratic functions change at different rates depending on where you are in the function's domain.
Compare your answer with the correct one above
Let  . Use linear approximation to estimate
. Use linear approximation to estimate  .
.
Let 

Note that:

Therefore, for values relatively close to 1, we can use the formula for dy (the differential form of the derivative) to estimate f at close values.
 From log derivative with chain rule.
From log derivative with chain rule.
Since  lies
lies  to the right of
to the right of  ,
,  and
and  for the estimation, so:
for the estimation, so:

So then:

Note that:
Therefore, for values relatively close to 1, we can use the formula for dy (the differential form of the derivative) to estimate f at close values.

Since 




So then:
Compare your answer with the correct one above
Using  , approximate the value of
, approximate the value of 
Using 
First, we need to rearrange the given to match the approximation formula.  Therefore,
Therefore, 
First, we need to rearrange the given to match the approximation formula. 
Compare your answer with the correct one above
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length  ?
?
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length 
Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:

The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:

Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:



Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:
The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:
Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:
Compare your answer with the correct one above
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length  ?
?
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length 
Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:

The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:

Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:



Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:
The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:
Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:
Compare your answer with the correct one above
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length  ?
?
A cube is diminishing in size. What is the ratio of the rate of loss of the cube's volume to the rate of loss of its sides when its sides have length 
Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:

The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:

Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:



Begin by writing the equations for a cube's dimensions. Namely its volume in terms of the length of its sides:
The rates of change of the volume can be found by taking the derivative of each side of the equation with respect to time:
Now, knowing the length of the sides, simply divide to find the ratio between the rate of change of the volume and sides:
Compare your answer with the correct one above
What is the area of the region bounded by  and
and  ?
?
What is the area of the region bounded by 

To find the area under the curve, we need to perform a definite integral. Essentially, this integral will be summing up all the infinitesimally small rectangles that make up the region. The entire region is in the first quadrant, so we don't have to worry about splitting our region up.
When we take the integral we will need to use,
 then plug in the upper and lower bounds into the function and take the difference.
then plug in the upper and lower bounds into the function and take the difference.
Therefore,

To find the area under the curve, we need to perform a definite integral. Essentially, this integral will be summing up all the infinitesimally small rectangles that make up the region. The entire region is in the first quadrant, so we don't have to worry about splitting our region up.
When we take the integral we will need to use,

Therefore,
Compare your answer with the correct one above
Find the area of the curve  from
from  to
to 

Find the area of the curve 


Written in words, solve:

To solve:
1. Find the indefinite integral of the function.
2. Plug in the upper and lower limit values and take the difference of the two values.
1. Using the power rule which states,
 to the term
to the term  and recalling the integral of
and recalling the integral of  is
is  we find,
we find,
 .
.
2. Plug in  and
and  for
for  and then take the difference.
and then take the difference.
 =
= 
note:

Written in words, solve:
To solve:
1. Find the indefinite integral of the function.
2. Plug in the upper and lower limit values and take the difference of the two values.
1. Using the power rule which states,





2. Plug in 



note:
Compare your answer with the correct one above
What is the average value of the function f(x) = 12x3 + 15x + 5 on the interval \[3, 6\]?
What is the average value of the function f(x) = 12x3 + 15x + 5 on the interval \[3, 6\]?
To find the average value, we must take the integral of f(x) between 3 and 6 and then multiply it by 1/(6 – 3) = 1/3.
The indefinite form of the integral is: 3x4 + 7.5x2 + 5x
The integral from 3 to 6 is therefore: (3(6)4 + 7.5(6)2 + 5(6)) - (3(3)4 + 7.5(3)2 + 5(3)) = (3888 + 270 + 30) – (243 + 22.5 + 15) = 3907.5
The average value is 3907.5/3 = 1302.5
To find the average value, we must take the integral of f(x) between 3 and 6 and then multiply it by 1/(6 – 3) = 1/3.
The indefinite form of the integral is: 3x4 + 7.5x2 + 5x
The integral from 3 to 6 is therefore: (3(6)4 + 7.5(6)2 + 5(6)) - (3(3)4 + 7.5(3)2 + 5(3)) = (3888 + 270 + 30) – (243 + 22.5 + 15) = 3907.5
The average value is 3907.5/3 = 1302.5
Compare your answer with the correct one above
Find the dot product of a = <2,2,-1> and b = <5,-3,2>.
Find the dot product of a = <2,2,-1> and b = <5,-3,2>.
To find the dot product, we multiply the individual corresponding components and add.
Here, the dot product is found by:
2 * 5 + 2 * (-3) + (-1) * 2 = 2.
To find the dot product, we multiply the individual corresponding components and add.
Here, the dot product is found by:
2 * 5 + 2 * (-3) + (-1) * 2 = 2.
Compare your answer with the correct one above