How to find if right triangles are congruent - Basic Geometry
Card 0 of 14
Which of the following is not sufficient to show that two right triangles are congruent?
Which of the following is not sufficient to show that two right triangles are congruent?
Two right triangles can have all the same angles and not be congruent, merely scaled larger or smaller. If all the side lengths are multiplied by the same number, the angles will remain unchanged, but the triangles will not be congruent.
Two right triangles can have all the same angles and not be congruent, merely scaled larger or smaller. If all the side lengths are multiplied by the same number, the angles will remain unchanged, but the triangles will not be congruent.
Compare your answer with the correct one above
Which of the following pieces of information would not allow the conclusion that


Which of the following pieces of information would not allow the conclusion that

To determine the answer choice that does not lead to congruence, we should simply use process of elimination.
If  , then subtracting tells us that
, then subtracting tells us that  .; therefore
.; therefore  . Given the fact that reflexively
. Given the fact that reflexively  and that both
and that both  and
and  are both right angles and thus congruent, we can establish congruence by way of Side-Angle-Side.
are both right angles and thus congruent, we can establish congruence by way of Side-Angle-Side.
Similarly, if  , then
, then  , and given the other information we determined with our last choice, we can establish conguence by way of Hypotenuse-Leg.
, and given the other information we determined with our last choice, we can establish conguence by way of Hypotenuse-Leg.
If  , given what we already know we can establish congruence by Angle-Angle-Side
, given what we already know we can establish congruence by Angle-Angle-Side
Finally, if  is an angle bisector, then our two halves are congruent.
is an angle bisector, then our two halves are congruent.  . Given what we know, we can establish congruence by Angle-Side-Angle
. Given what we know, we can establish congruence by Angle-Side-Angle
The only remaining choice is the case where  . This does not tell us how the two parts of this angle are related, we lack enough information for congruence.
. This does not tell us how the two parts of this angle are related, we lack enough information for congruence.
To determine the answer choice that does not lead to congruence, we should simply use process of elimination.
If 





Similarly, if 

If 
Finally, if 

The only remaining choice is the case where 
Compare your answer with the correct one above
Complete the congruence statement


Complete the congruence statement

Since we know that  , we know that
, we know that  is also a right angle and is thus congruent to
is also a right angle and is thus congruent to  .
.
We are given that  . Furthermore, since
. Furthermore, since  and
and  are vertical angles, they are also congruent.
are vertical angles, they are also congruent.
Therefore, we have enough evidence to conclude congruence by Angle-Side-Angle. Vertex  matches up with
matches up with  , vertex
, vertex  matches up with
matches up with  , and
, and  matches up to
matches up to  . Thus, our congruence statement should look the following
. Thus, our congruence statement should look the following

Since we know that 


We are given that 


Therefore, we have enough evidence to conclude congruence by Angle-Side-Angle. Vertex 





Compare your answer with the correct one above
Figures  and
and  are triangles.
are triangles.



Are  and
and  congruent?
congruent?
Figures 


Are 

We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal, and the measures of two angles. We know that  and
and  because the sum of the angles of a triangle must equal
because the sum of the angles of a triangle must equal  . So the corresponding angles are also equal. Therefore, the triangles are congruent.
. So the corresponding angles are also equal. Therefore, the triangles are congruent.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal, and the measures of two angles. We know that 


Compare your answer with the correct one above
Figures  and
and  are triangles.
are triangles.


Are  and
and  congruent?
congruent?
Figures 


Are 

We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of  . A triangle whose sides are in this ratio is a
. A triangle whose sides are in this ratio is a  , where the shortest side lies opposite the
, where the shortest side lies opposite the  angle, the longest side is the hypotenuse and lies opposite the right angle, and the third side lies opposite the
angle, the longest side is the hypotenuse and lies opposite the right angle, and the third side lies opposite the  angle. (Remember
angle. (Remember  .) So we know the corresponding angles are equal. Therefore, the triangles are congruent.
.) So we know the corresponding angles are equal. Therefore, the triangles are congruent.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of 




Compare your answer with the correct one above
Figures  and
and  are triangles.
are triangles.


Are  and
and  congruent?
congruent?
Figures 


Are 

We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of  .
.
Simplify the ratio by dividing by 




Thus, the corresponding sides are in the ratio  and we know both triangles are
and we know both triangles are  triangles. Since the corresponding angles and the corresponding sides are equal, the triangles are congruent.
triangles. Since the corresponding angles and the corresponding sides are equal, the triangles are congruent.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of 
Simplify the ratio by dividing by
Thus, the corresponding sides are in the ratio 

Compare your answer with the correct one above
Figures  and
and  are triangles.
are triangles.



Are  and
and  congruent?
congruent?
Figures 


Are 

We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal, and the measures of two angles. We know that  and
and  because the sum of the angles of a triangle must equal
because the sum of the angles of a triangle must equal  . So the corresponding angles are also equal. Therefore, the triangles are congruent.
. So the corresponding angles are also equal. Therefore, the triangles are congruent.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal, and the measures of two angles. We know that 


Compare your answer with the correct one above
Figures  and
and  are triangles.
are triangles.


Are  and
and  congruent?
congruent?
Figures 


Are 

We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of  . A triangle whose sides are in this ratio is a
. A triangle whose sides are in this ratio is a  , where the shorter sides lies opposite the
, where the shorter sides lies opposite the  angles, and the longer side is the hypotenuse and lies opposite the right angle. So we know the corresponding angles are equal. Therefore, the triangles are congruent.
angles, and the longer side is the hypotenuse and lies opposite the right angle. So we know the corresponding angles are equal. Therefore, the triangles are congruent.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of 


Compare your answer with the correct one above
Figures  and
and  are triangles.
are triangles.


Are  and
and  congruent?
congruent?
Figures 


Are 

We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of  .
.
Simplify the ratio by dividing by 



Thus, the corresponding sides are in the ratio  and we know both triangles are
and we know both triangles are  triangles. Since the corresponding angles and the corresponding sides are equal, the triangles are congruent.
triangles. Since the corresponding angles and the corresponding sides are equal, the triangles are congruent.
We know that congruent triangles have equal corresponding angles and equal corresponding sides. We are given that the corresponding sides are equal and are in the ratio of 
Simplify the ratio by dividing by
Thus, the corresponding sides are in the ratio 

Compare your answer with the correct one above
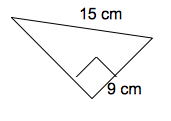
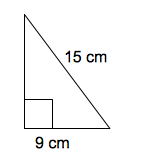
Are these right triangles congruent?

Are these right triangles congruent?
Right now we can't directly compare these triangles because we do not know all three side lengths. However, we can use Pythagorean Theorem to determine both missing sides. The left triangle is missing the hypotenuse:




The right triangle is missing one of the legs:

 subtract 2,304 from both sides
subtract 2,304 from both sides


This means that the two triangles both have side lengths 48, 55, 73, so they must be congruent.
Right now we can't directly compare these triangles because we do not know all three side lengths. However, we can use Pythagorean Theorem to determine both missing sides. The left triangle is missing the hypotenuse:
The right triangle is missing one of the legs:

This means that the two triangles both have side lengths 48, 55, 73, so they must be congruent.
Compare your answer with the correct one above
The hypotenuse and acute angle are given for several triangles. Which if any are congruent? Triangle A- Hypotenuse=15; acute angle=56 degrees. Triangle B- Hypotenuse=18; acute angle=56 degrees. Triangle C-Hypotenuse=18; acute angle= 45 degrees.
The hypotenuse and acute angle are given for several triangles. Which if any are congruent? Triangle A- Hypotenuse=15; acute angle=56 degrees. Triangle B- Hypotenuse=18; acute angle=56 degrees. Triangle C-Hypotenuse=18; acute angle= 45 degrees.
The correct answer is none of these. There are several pairs of angles and sides or sides and angles that must be the same in order for two triangles to be congruent.
In our case, we need the acute angle and the hypotenuse to both be equal. No two triangles above have this relationship and therefore no two are congruent.
The correct answer is none of these. There are several pairs of angles and sides or sides and angles that must be the same in order for two triangles to be congruent.
In our case, we need the acute angle and the hypotenuse to both be equal. No two triangles above have this relationship and therefore no two are congruent.
Compare your answer with the correct one above
Given:  and
and  .
.
 and
and  are both right angles.
are both right angles.


True or false: From the above information, it follows that  .
.
Given: 



True or false: From the above information, it follows that 
If we seek to prove that  , then
, then  ,
,  , and
, and  correspond to
correspond to  ,
,  , and
, and  , respectively.
, respectively.
By the Hypotenuse-Leg Theorem (HL), if the hypotenuse and one leg of a triangle are congruent to those of another, the triangles are congruent.
 and
and  are both right angles, so
are both right angles, so  and
and  are both right triangles.
are both right triangles.  and
and  are congruent corresponding sides, and moreover, since, each includes the right-angle vertex as an endpoint, they are congruent corresponding legs.
are congruent corresponding sides, and moreover, since, each includes the right-angle vertex as an endpoint, they are congruent corresponding legs.  and
and  are opposite the right angles, making them congruent corresponding hypotenuses.
are opposite the right angles, making them congruent corresponding hypotenuses.
The conditions of HL are satisfied, so  .
.
If we seek to prove that 






By the Hypotenuse-Leg Theorem (HL), if the hypotenuse and one leg of a triangle are congruent to those of another, the triangles are congruent.








The conditions of HL are satisfied, so 
Compare your answer with the correct one above
Given:  and
and  .
.
 and
and  are both right angles.
are both right angles.


True or false: From the given information, it follows that  .
.
Given: 



True or false: From the given information, it follows that 
The congruence of  and
and  cannot be proved from the given information alone. Examine the two triangles below:
cannot be proved from the given information alone. Examine the two triangles below:

 ,
,  , and
, and  and
and  are both right angles, so the conditions of the problem are met; however, since the sides are not congruent between triangles - for example,
are both right angles, so the conditions of the problem are met; however, since the sides are not congruent between triangles - for example,  - the triangles are not congruent either.
- the triangles are not congruent either.
The congruence of 







Compare your answer with the correct one above