Understanding Electrostatics - AP Physics C Electricity & Magnetism
Card 0 of 8
A hollow metal sphere with a diameter of 10cm has a net charge of 
distributed uniformly across its surface. What is the magnitude of the field a distance 2.0m from the center of the sphere?
A hollow metal sphere with a diameter of 10cm has a net charge of
Relevant equations:
(electric field of point charge)
Anywhere outside the metal sphere, the electric field is the same as it would be for a point charge of the same magnitude, located at the center of the sphere. So, calculate the electric field of a point charge given:
Plugging in gives:
Relevant equations:
Anywhere outside the metal sphere, the electric field is the same as it would be for a point charge of the same magnitude, located at the center of the sphere. So, calculate the electric field of a point charge given:
Plugging in gives:
Compare your answer with the correct one above
Two infinite parallel conducting sheets each have positive charge density 
. What is the magnitude and direction of the electric field to the right of the right sheet?
Two infinite parallel conducting sheets each have positive charge density
Relevant equations:
(field due to single infinite plane)
Electric field is additive; in other words, the total electric field from the two planes is the sum of their individual fields:
The direction of the electric field is away from positive source charges. Thus, to the right of these positively charged planes, the field points away to the right.
Relevant equations:
Electric field is additive; in other words, the total electric field from the two planes is the sum of their individual fields:
The direction of the electric field is away from positive source charges. Thus, to the right of these positively charged planes, the field points away to the right.
Compare your answer with the correct one above
Consider a spherical capacitor made of two nested spheres. The smaller sphere has a radius of 
and a charge of 
, and lies within a larger sphere with radius 
and a charge of 
.
Which of the following equations accurately describes the capacitance of this spherical capacitor?
Consider a spherical capacitor made of two nested spheres. The smaller sphere has a radius of
Which of the following equations accurately describes the capacitance of this spherical capacitor?
To solve this problem, we will need to derive an equation.
We know that:
We can use Gauss's law to derive the electric field between the two circles yielding:
Doing our integration with respect to 
from 
to 
, we get:
We can plug this back into our equation for capacitance to get:
To solve this problem, we will need to derive an equation.
We know that:
We can use Gauss's law to derive the electric field between the two circles yielding:
Doing our integration with respect to
We can plug this back into our equation for capacitance to get:
Compare your answer with the correct one above
Four particles, each of charge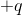 
, make up the four corners of a square with equal side lengths of 
. For the charge in the top left corner of the square, in what direction is the net force that it experiences due to its interactions with the other three particles?
Four particles, each of charge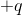
The correct answer is 45 degrees upwards of left. Since all particles have charge 
, all forces will be repulsive (there will be no attracting forces). The particle in the top-right corner creates a repulsive force directly to the left, and the particle in the bottom-left corner creates a repulsive force directly upwards. These are equal in magnitude, since they are both at distance 
from the top left corner. The bottom-right corner also creates a repulsive force, but acts along the same direction as the vector sum of a leftwards and upwards force.
The correct answer is 45 degrees upwards of left. Since all particles have charge
Compare your answer with the correct one above
A hollow metal sphere with a diameter of 10cm has a net charge of distributed uniformly across its surface. What is the magnitude of the field a distance 2.0m from the center of the sphere?
A hollow metal sphere with a diameter of 10cm has a net charge of
Relevant equations:
(electric field of point charge)
Anywhere outside the metal sphere, the electric field is the same as it would be for a point charge of the same magnitude, located at the center of the sphere. So, calculate the electric field of a point charge given:
Plugging in gives:
Relevant equations:
Anywhere outside the metal sphere, the electric field is the same as it would be for a point charge of the same magnitude, located at the center of the sphere. So, calculate the electric field of a point charge given:
Plugging in gives:
Compare your answer with the correct one above
Two infinite parallel conducting sheets each have positive charge density . What is the magnitude and direction of the electric field to the right of the right sheet?
Two infinite parallel conducting sheets each have positive charge density
Relevant equations:
(field due to single infinite plane)
Electric field is additive; in other words, the total electric field from the two planes is the sum of their individual fields:
The direction of the electric field is away from positive source charges. Thus, to the right of these positively charged planes, the field points away to the right.
Relevant equations:
Electric field is additive; in other words, the total electric field from the two planes is the sum of their individual fields:
The direction of the electric field is away from positive source charges. Thus, to the right of these positively charged planes, the field points away to the right.
Compare your answer with the correct one above
Consider a spherical capacitor made of two nested spheres. The smaller sphere has a radius of and a charge of , and lies within a larger sphere with radius and a charge of .
Which of the following equations accurately describes the capacitance of this spherical capacitor?
Consider a spherical capacitor made of two nested spheres. The smaller sphere has a radius of
Which of the following equations accurately describes the capacitance of this spherical capacitor?
To solve this problem, we will need to derive an equation.
We know that:
We can use Gauss's law to derive the electric field between the two circles yielding:
Doing our integration with respect to from to , we get:
We can plug this back into our equation for capacitance to get:
To solve this problem, we will need to derive an equation.
We know that:
We can use Gauss's law to derive the electric field between the two circles yielding:
Doing our integration with respect to
We can plug this back into our equation for capacitance to get:
Compare your answer with the correct one above
Four particles, each of charge 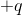, make up the four corners of a square with equal side lengths of . For the charge in the top left corner of the square, in what direction is the net force that it experiences due to its interactions with the other three particles?
Four particles, each of charge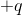
The correct answer is 45 degrees upwards of left. Since all particles have charge , all forces will be repulsive (there will be no attracting forces). The particle in the top-right corner creates a repulsive force directly to the left, and the particle in the bottom-left corner creates a repulsive force directly upwards. These are equal in magnitude, since they are both at distance from the top left corner. The bottom-right corner also creates a repulsive force, but acts along the same direction as the vector sum of a leftwards and upwards force.
The correct answer is 45 degrees upwards of left. Since all particles have charge
Compare your answer with the correct one above