Circular and Rotational Motion - AP Physics C Electricity & Magnetism
Card 0 of 20
A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?
A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?
The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.

Remember that centripetal acceleration is given by the following equation.

Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.

Since we're trying to find the speed of the ball, we solve for v.

We know the following information from the question.



We can use this information in our equation to solve for the speed of the ball.


The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.
Remember that centripetal acceleration is given by the following equation.
Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.
Since we're trying to find the speed of the ball, we solve for v.
We know the following information from the question.
We can use this information in our equation to solve for the speed of the ball.
Compare your answer with the correct one above
In uniform circular motion, the net force is always directed ___________.
In uniform circular motion, the net force is always directed ___________.
The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.

In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.
The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.
In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.
Compare your answer with the correct one above
A car moves around a circular path of radius 100m at a velocity of  . What is the coefficient of friction between the car and the road?
. What is the coefficient of friction between the car and the road?
A car moves around a circular path of radius 100m at a velocity of 
The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.



We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:


We can use our given values to solve:

The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.
We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:
We can use our given values to solve:
Compare your answer with the correct one above
An object of mass 10kg undergoes uniform circular motion with a constant velocity of  at a radius of 10m. How long does it take for the object to make one full revolution?
at a radius of 10m. How long does it take for the object to make one full revolution?
An object of mass 10kg undergoes uniform circular motion with a constant velocity of 
The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation:

Use the given radius and velocity to solve for the time per revolution:

The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation:
Use the given radius and velocity to solve for the time per revolution:
Compare your answer with the correct one above
A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?
A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?
The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.

Remember that centripetal acceleration is given by the following equation.

Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.

Since we're trying to find the speed of the ball, we solve for v.

We know the following information from the question.



We can use this information in our equation to solve for the speed of the ball.


The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.
Remember that centripetal acceleration is given by the following equation.
Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.
Since we're trying to find the speed of the ball, we solve for v.
We know the following information from the question.
We can use this information in our equation to solve for the speed of the ball.
Compare your answer with the correct one above
In uniform circular motion, the net force is always directed ___________.
In uniform circular motion, the net force is always directed ___________.
The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.

In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.
The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.
In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.
Compare your answer with the correct one above
A car moves around a circular path of radius 100m at a velocity of  . What is the coefficient of friction between the car and the road?
. What is the coefficient of friction between the car and the road?
A car moves around a circular path of radius 100m at a velocity of 
The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.



We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:


We can use our given values to solve:

The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.
We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:
We can use our given values to solve:
Compare your answer with the correct one above
An object of mass 10kg undergoes uniform circular motion with a constant velocity of  at a radius of 10m. How long does it take for the object to make one full revolution?
at a radius of 10m. How long does it take for the object to make one full revolution?
An object of mass 10kg undergoes uniform circular motion with a constant velocity of 
The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation:

Use the given radius and velocity to solve for the time per revolution:

The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation:
Use the given radius and velocity to solve for the time per revolution:
Compare your answer with the correct one above

A ball of mass  is tied to a rope and moves along a horizontal circular path of radius
is tied to a rope and moves along a horizontal circular path of radius  as shown in the diagram (view from above). The maximum tension the rope can stand before breaking is given by
as shown in the diagram (view from above). The maximum tension the rope can stand before breaking is given by  . Which of the following represents the ball's linear velocity given that the rope does not break?
. Which of the following represents the ball's linear velocity given that the rope does not break?

A ball of mass 


This is a centripetal force problem. In this case the tension on the rope is the centripetal force that keeps the ball moving on a circle.
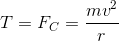
If we want for the rope not to break, then the tension should never exceed  .
.

Now we just solve for velocity:

This is a centripetal force problem. In this case the tension on the rope is the centripetal force that keeps the ball moving on a circle.
If we want for the rope not to break, then the tension should never exceed 
Now we just solve for velocity:
Compare your answer with the correct one above

A ball of mass  is tied to a rope and moves along a horizontal circular path of radius
is tied to a rope and moves along a horizontal circular path of radius  as shown in the diagram (view from above). The maximum tension the rope can stand before breaking is given by
as shown in the diagram (view from above). The maximum tension the rope can stand before breaking is given by  . Which of the following represents the ball's linear velocity given that the rope does not break?
. Which of the following represents the ball's linear velocity given that the rope does not break?

A ball of mass 


This is a centripetal force problem. In this case the tension on the rope is the centripetal force that keeps the ball moving on a circle.
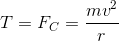
If we want for the rope not to break, then the tension should never exceed  .
.

Now we just solve for velocity:

This is a centripetal force problem. In this case the tension on the rope is the centripetal force that keeps the ball moving on a circle.
If we want for the rope not to break, then the tension should never exceed 
Now we just solve for velocity:
Compare your answer with the correct one above
A mechanic is using a wrench to loosen and tighten screws on an engine block and wants to increase the amount of torque he puts on the screws to adjust them more easily. Which of the following steps will not help him to do so?
A mechanic is using a wrench to loosen and tighten screws on an engine block and wants to increase the amount of torque he puts on the screws to adjust them more easily. Which of the following steps will not help him to do so?
Remember the torque equation:

Exerting force on the wrench at an angle less perpendicular to the wrench will reduce  and thus reduce the torque.
and thus reduce the torque.
The other answer options will all increase the torque being applied, making the twisting motion easier.
Remember the torque equation:
Exerting force on the wrench at an angle less perpendicular to the wrench will reduce 
The other answer options will all increase the torque being applied, making the twisting motion easier.
Compare your answer with the correct one above
A mechanic is using a wrench to loosen and tighten screws on an engine block and wants to increase the amount of torque he puts on the screws to adjust them more easily. Which of the following steps will not help him to do so?
A mechanic is using a wrench to loosen and tighten screws on an engine block and wants to increase the amount of torque he puts on the screws to adjust them more easily. Which of the following steps will not help him to do so?
Remember the torque equation:

Exerting force on the wrench at an angle less perpendicular to the wrench will reduce  and thus reduce the torque.
and thus reduce the torque.
The other answer options will all increase the torque being applied, making the twisting motion easier.
Remember the torque equation:
Exerting force on the wrench at an angle less perpendicular to the wrench will reduce 
The other answer options will all increase the torque being applied, making the twisting motion easier.
Compare your answer with the correct one above
Doing which of the following would allow you to find the center of mass of an object?
Doing which of the following would allow you to find the center of mass of an object?
Center of mass can be found by spinning an object. It will naturally spin around its center of mass, due to the concept of even distribution of mass in relation to the center of mass. Shape and mass are important factors in this property, but the most improtant factor is the mass distribution.
Center of mass can be found by spinning an object. It will naturally spin around its center of mass, due to the concept of even distribution of mass in relation to the center of mass. Shape and mass are important factors in this property, but the most improtant factor is the mass distribution.
Compare your answer with the correct one above
If two masses,  and
and  are placed on a seesaw of length
are placed on a seesaw of length  , where must the fulcrum be placed such that the seesaw remains level?
, where must the fulcrum be placed such that the seesaw remains level?
If two masses, 


This question asks us to find the center of mass for this system. We know that the center of mass resides a distance  from the first mass such that:
from the first mass such that:

In this case:


Plug in known values and solve.

This question asks us to find the center of mass for this system. We know that the center of mass resides a distance 
In this case:
Plug in known values and solve.
Compare your answer with the correct one above
If the fulcrum of a balanced scale is shifted to the left, what type of adjustment must be made to rebalance the scale?
If the fulcrum of a balanced scale is shifted to the left, what type of adjustment must be made to rebalance the scale?
Changing the position of the fulcrum by moving it to the left means the center of mass will be to the right of the new position. Therefore, the scale will tip right. Adding more mass to the left end will rebalance the scale. None of the other options make sense. Adding more mass to the new fulcrum position will not change the balance of the scale because that mass is a negligible distance from the new fulcrum position and does nothing to change the masses on either side.
Changing the position of the fulcrum by moving it to the left means the center of mass will be to the right of the new position. Therefore, the scale will tip right. Adding more mass to the left end will rebalance the scale. None of the other options make sense. Adding more mass to the new fulcrum position will not change the balance of the scale because that mass is a negligible distance from the new fulcrum position and does nothing to change the masses on either side.
Compare your answer with the correct one above
Three  point masses are at the points
point masses are at the points  ,
,  and
and
 and a
and a  point mass is at the point
point mass is at the point  .
.
How far from the origin is the center of mass of the system?
Three 





How far from the origin is the center of mass of the system?
To find the center of mass, we have to take the weighted average of the x coordinates and the y coordinates.
 Measures:
Measures:  Measures
Measures




First, we take the weighted measurement of the x-axis:

We can see that the result of the x-axis contribution is equal to  .
.
Now, let's look at the y-axis contribution:

This equals to 
Now that we have the x and y components, we take the root of squares to get the final answer:

This will give us 
To find the center of mass, we have to take the weighted average of the x coordinates and the y coordinates.



First, we take the weighted measurement of the x-axis:
We can see that the result of the x-axis contribution is equal to 
Now, let's look at the y-axis contribution:
This equals to
Now that we have the x and y components, we take the root of squares to get the final answer:
This will give us
Compare your answer with the correct one above
Doing which of the following would allow you to find the center of mass of an object?
Doing which of the following would allow you to find the center of mass of an object?
Center of mass can be found by spinning an object. It will naturally spin around its center of mass, due to the concept of even distribution of mass in relation to the center of mass. Shape and mass are important factors in this property, but the most improtant factor is the mass distribution.
Center of mass can be found by spinning an object. It will naturally spin around its center of mass, due to the concept of even distribution of mass in relation to the center of mass. Shape and mass are important factors in this property, but the most improtant factor is the mass distribution.
Compare your answer with the correct one above
If two masses,  and
and  are placed on a seesaw of length
are placed on a seesaw of length  , where must the fulcrum be placed such that the seesaw remains level?
, where must the fulcrum be placed such that the seesaw remains level?
If two masses, 


This question asks us to find the center of mass for this system. We know that the center of mass resides a distance  from the first mass such that:
from the first mass such that:

In this case:


Plug in known values and solve.

This question asks us to find the center of mass for this system. We know that the center of mass resides a distance 
In this case:
Plug in known values and solve.
Compare your answer with the correct one above
If the fulcrum of a balanced scale is shifted to the left, what type of adjustment must be made to rebalance the scale?
If the fulcrum of a balanced scale is shifted to the left, what type of adjustment must be made to rebalance the scale?
Changing the position of the fulcrum by moving it to the left means the center of mass will be to the right of the new position. Therefore, the scale will tip right. Adding more mass to the left end will rebalance the scale. None of the other options make sense. Adding more mass to the new fulcrum position will not change the balance of the scale because that mass is a negligible distance from the new fulcrum position and does nothing to change the masses on either side.
Changing the position of the fulcrum by moving it to the left means the center of mass will be to the right of the new position. Therefore, the scale will tip right. Adding more mass to the left end will rebalance the scale. None of the other options make sense. Adding more mass to the new fulcrum position will not change the balance of the scale because that mass is a negligible distance from the new fulcrum position and does nothing to change the masses on either side.
Compare your answer with the correct one above
Three  point masses are at the points
point masses are at the points  ,
,  and
and
 and a
and a  point mass is at the point
point mass is at the point  .
.
How far from the origin is the center of mass of the system?
Three 





How far from the origin is the center of mass of the system?
To find the center of mass, we have to take the weighted average of the x coordinates and the y coordinates.
 Measures:
Measures:  Measures
Measures




First, we take the weighted measurement of the x-axis:

We can see that the result of the x-axis contribution is equal to  .
.
Now, let's look at the y-axis contribution:

This equals to 
Now that we have the x and y components, we take the root of squares to get the final answer:

This will give us 
To find the center of mass, we have to take the weighted average of the x coordinates and the y coordinates.



First, we take the weighted measurement of the x-axis:
We can see that the result of the x-axis contribution is equal to 
Now, let's look at the y-axis contribution:
This equals to
Now that we have the x and y components, we take the root of squares to get the final answer:
This will give us
Compare your answer with the correct one above