Motion - AP Physics C Electricity & Magnetism
Card 0 of 20
A man runs with a velocity described by the function below.

What is the function for his acceleration?
A man runs with a velocity described by the function below.
What is the function for his acceleration?
The function for acceleration is the derivative of the function for velocity.



The function for acceleration is the derivative of the function for velocity.
Compare your answer with the correct one above
A man runs with a velocity as described by the function below.

How far does he travel in 1 minute?
A man runs with a velocity as described by the function below.
How far does he travel in 1 minute?
Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.



Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.
Compare your answer with the correct one above
A particle traveling in a straight line accelerates uniformly from rest to  in
in  and then continues at constant speed for an additional for an additional
and then continues at constant speed for an additional for an additional  . What is the total distance traveled by the particle during the
. What is the total distance traveled by the particle during the  ?
?
A particle traveling in a straight line accelerates uniformly from rest to 



First off we have to convert  to meters per second.
to meters per second.

Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be  . The acceleration of the object at this time can be calculated using:
. The acceleration of the object at this time can be calculated using:
 , substituting the values, we get:
, substituting the values, we get:

Next, we use the distance equation to find the distance in the first 5 seconds:

 because the initial speed is
because the initial speed is  .
.
If we plug in  ,
,  , we get:
, we get: 
Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:

 in this case is not equal to
in this case is not equal to  , it is equal to
, it is equal to  and
and 
Plugging in the equation, we get 
Adding  and
and  we get the total distance to be
we get the total distance to be 
First off we have to convert 
Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be 

Next, we use the distance equation to find the distance in the first 5 seconds:


If we plug in 

Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:



Plugging in the equation, we get
Adding 

Compare your answer with the correct one above
A man runs with a velocity described by the function below.

What is the function for his acceleration?
A man runs with a velocity described by the function below.
What is the function for his acceleration?
The function for acceleration is the derivative of the function for velocity.



The function for acceleration is the derivative of the function for velocity.
Compare your answer with the correct one above
A man runs with a velocity as described by the function below.

How far does he travel in 1 minute?
A man runs with a velocity as described by the function below.
How far does he travel in 1 minute?
Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.



Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.
Compare your answer with the correct one above
A particle traveling in a straight line accelerates uniformly from rest to  in
in  and then continues at constant speed for an additional for an additional
and then continues at constant speed for an additional for an additional  . What is the total distance traveled by the particle during the
. What is the total distance traveled by the particle during the  ?
?
A particle traveling in a straight line accelerates uniformly from rest to 



First off we have to convert  to meters per second.
to meters per second.

Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be  . The acceleration of the object at this time can be calculated using:
. The acceleration of the object at this time can be calculated using:
 , substituting the values, we get:
, substituting the values, we get:

Next, we use the distance equation to find the distance in the first 5 seconds:

 because the initial speed is
because the initial speed is  .
.
If we plug in  ,
,  , we get:
, we get: 
Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:

 in this case is not equal to
in this case is not equal to  , it is equal to
, it is equal to  and
and 
Plugging in the equation, we get 
Adding  and
and  we get the total distance to be
we get the total distance to be 
First off we have to convert 
Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be 

Next, we use the distance equation to find the distance in the first 5 seconds:


If we plug in 

Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:



Plugging in the equation, we get
Adding 

Compare your answer with the correct one above
A  ball is thrown horizontally from the top of a
ball is thrown horizontally from the top of a 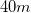 high building. It has an initial velocity of
high building. It has an initial velocity of 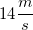 and lands on the ground
and lands on the ground  away from the base of the building. Assuming air resistance is negligible, which of the following changes would cause the range of this projectile to increase?
away from the base of the building. Assuming air resistance is negligible, which of the following changes would cause the range of this projectile to increase?
I. Increasing the initial horizontal velocity
II. Decreasing the mass of the ball
III. Throwing the ball from an identical building on the moon
A 
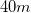
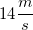

I. Increasing the initial horizontal velocity
II. Decreasing the mass of the ball
III. Throwing the ball from an identical building on the moon
Relevant equations:


Choice I is true because  is proportional to the range
is proportional to the range  , so increasing
, so increasing  increases
increases  if
if  is constant. This relationship is given by the equation:
is constant. This relationship is given by the equation:

Choice II is false because the motion of a projectile is independent of mass.
Choice III is true because the vertical acceleration on the moon  would be less. Decreasing
would be less. Decreasing 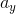 increases the time the ball is in the air, thereby increasing
increases the time the ball is in the air, thereby increasing  if
if  is constant. This relationship is also shown in the equation:
is constant. This relationship is also shown in the equation:

Relevant equations:
Choice I is true because 




Choice II is false because the motion of a projectile is independent of mass.
Choice III is true because the vertical acceleration on the moon 
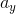


Compare your answer with the correct one above
Water emerges horizontally from a hole in a tank 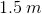 above the ground. If the water hits the ground
above the ground. If the water hits the ground 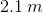 from the base of the tank, at what speed is the water emerging from the hole? (Hint: Treat the water droplets as projectiles.)
from the base of the tank, at what speed is the water emerging from the hole? (Hint: Treat the water droplets as projectiles.)
Water emerges horizontally from a hole in a tank 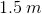
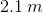
To understand this problem, we have to understand that the water has a x-velocity and a y-veloctiy. The x-velocity never changes.
First we want to find the time it took for the water to hit the ground. We can use this equation: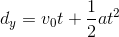
We know that the y-velocity is 0 to start with, acceleration is  and
and  .
.
Substituting into the equation, we get:

Next we have to substitute the time into the equation for the x component

We know that  and
and 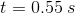 , so we can conclude that:
, so we can conclude that:
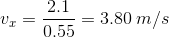
To understand this problem, we have to understand that the water has a x-velocity and a y-veloctiy. The x-velocity never changes.
First we want to find the time it took for the water to hit the ground. We can use this equation:
We know that the y-velocity is 0 to start with, acceleration is 

Substituting into the equation, we get:
Next we have to substitute the time into the equation for the x component
We know that 
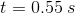
Compare your answer with the correct one above
A  ball is thrown horizontally from the top of a
ball is thrown horizontally from the top of a 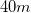 high building. It has an initial velocity of
high building. It has an initial velocity of 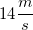 and lands on the ground
and lands on the ground  away from the base of the building. Assuming air resistance is negligible, which of the following changes would cause the range of this projectile to increase?
away from the base of the building. Assuming air resistance is negligible, which of the following changes would cause the range of this projectile to increase?
I. Increasing the initial horizontal velocity
II. Decreasing the mass of the ball
III. Throwing the ball from an identical building on the moon
A 
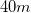
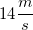

I. Increasing the initial horizontal velocity
II. Decreasing the mass of the ball
III. Throwing the ball from an identical building on the moon
Relevant equations:


Choice I is true because  is proportional to the range
is proportional to the range  , so increasing
, so increasing  increases
increases  if
if  is constant. This relationship is given by the equation:
is constant. This relationship is given by the equation:

Choice II is false because the motion of a projectile is independent of mass.
Choice III is true because the vertical acceleration on the moon  would be less. Decreasing
would be less. Decreasing 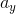 increases the time the ball is in the air, thereby increasing
increases the time the ball is in the air, thereby increasing  if
if  is constant. This relationship is also shown in the equation:
is constant. This relationship is also shown in the equation:

Relevant equations:
Choice I is true because 




Choice II is false because the motion of a projectile is independent of mass.
Choice III is true because the vertical acceleration on the moon 


Compare your answer with the correct one above
Water emerges horizontally from a hole in a tank 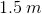 above the ground. If the water hits the ground
above the ground. If the water hits the ground 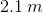 from the base of the tank, at what speed is the water emerging from the hole? (Hint: Treat the water droplets as projectiles.)
from the base of the tank, at what speed is the water emerging from the hole? (Hint: Treat the water droplets as projectiles.)
Water emerges horizontally from a hole in a tank 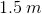
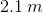
To understand this problem, we have to understand that the water has a x-velocity and a y-veloctiy. The x-velocity never changes.
First we want to find the time it took for the water to hit the ground. We can use this equation: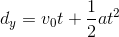
We know that the y-velocity is 0 to start with, acceleration is  and
and  .
.
Substituting into the equation, we get:

Next we have to substitute the time into the equation for the x component

We know that  and
and 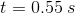 , so we can conclude that:
, so we can conclude that:
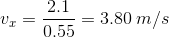
To understand this problem, we have to understand that the water has a x-velocity and a y-veloctiy. The x-velocity never changes.
First we want to find the time it took for the water to hit the ground. We can use this equation:
We know that the y-velocity is 0 to start with, acceleration is 

Substituting into the equation, we get:
Next we have to substitute the time into the equation for the x component
We know that 
Compare your answer with the correct one above
A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?
A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?
The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.

Remember that centripetal acceleration is given by the following equation.

Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.

Since we're trying to find the speed of the ball, we solve for v.

We know the following information from the question.



We can use this information in our equation to solve for the speed of the ball.


The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.
Remember that centripetal acceleration is given by the following equation.
Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.
Since we're trying to find the speed of the ball, we solve for v.
We know the following information from the question.
We can use this information in our equation to solve for the speed of the ball.
Compare your answer with the correct one above
In uniform circular motion, the net force is always directed ___________.
In uniform circular motion, the net force is always directed ___________.
The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.

In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.
The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.
In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.
Compare your answer with the correct one above
A car moves around a circular path of radius 100m at a velocity of  . What is the coefficient of friction between the car and the road?
. What is the coefficient of friction between the car and the road?
A car moves around a circular path of radius 100m at a velocity of 
The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.



We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:


We can use our given values to solve:

The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.
We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:
We can use our given values to solve:
Compare your answer with the correct one above
An object of mass 10kg undergoes uniform circular motion with a constant velocity of  at a radius of 10m. How long does it take for the object to make one full revolution?
at a radius of 10m. How long does it take for the object to make one full revolution?
An object of mass 10kg undergoes uniform circular motion with a constant velocity of 
The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation:

Use the given radius and velocity to solve for the time per revolution:

The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation:
Use the given radius and velocity to solve for the time per revolution:
Compare your answer with the correct one above
A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?
A 1.6kg ball is attached to a 1.8m string and is swinging in circular motion horizontally at the string's full length. If the string can withstand a tension force of 87N, what is the maximum speed the ball can travel without the string breaking?
The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.

Remember that centripetal acceleration is given by the following equation.

Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.

Since we're trying to find the speed of the ball, we solve for v.

We know the following information from the question.



We can use this information in our equation to solve for the speed of the ball.


The ball is experiencing centripetal force so that it can travel in a circular path. This centripetal force is written as the equation below.
Remember that centripetal acceleration is given by the following equation.
Since the centripetal force is coming from the tension of the string, set the tension force equal to the centripetal force.
Since we're trying to find the speed of the ball, we solve for v.
We know the following information from the question.
We can use this information in our equation to solve for the speed of the ball.
Compare your answer with the correct one above
In uniform circular motion, the net force is always directed ___________.
In uniform circular motion, the net force is always directed ___________.
The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.

In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.
The correct answer is "toward the center of the circle." Newton's second law tells us that the direction of the net force will be the same as the direction of the acceleration of the object.
In uniform circular motion, the object accelerates towards the center of the circle (centripetal acceleration); the net force acts in the same direction.
Compare your answer with the correct one above
A car moves around a circular path of radius 100m at a velocity of  . What is the coefficient of friction between the car and the road?
. What is the coefficient of friction between the car and the road?
A car moves around a circular path of radius 100m at a velocity of 
The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.



We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:


We can use our given values to solve:

The force of friction is what keeps the car in circular motion, preventing it from flying off the track. In other words, the frictional force will be equal to the centripetal force.
We can cancel mass from either side of the equation and rearrange to solve for the coefficient of friction:
We can use our given values to solve:
Compare your answer with the correct one above
An object of mass 10kg undergoes uniform circular motion with a constant velocity of  at a radius of 10m. How long does it take for the object to make one full revolution?
at a radius of 10m. How long does it take for the object to make one full revolution?
An object of mass 10kg undergoes uniform circular motion with a constant velocity of 
The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation:

Use the given radius and velocity to solve for the time per revolution:

The time for one full revolution can be calculated simply by manipulating the defintion of velocity, where the distance is just the circumference of the circlular path. The time it takes is modeled by the following equation:
Use the given radius and velocity to solve for the time per revolution:
Compare your answer with the correct one above

A ball of mass  is tied to a rope and moves along a horizontal circular path of radius
is tied to a rope and moves along a horizontal circular path of radius  as shown in the diagram (view from above). The maximum tension the rope can stand before breaking is given by
as shown in the diagram (view from above). The maximum tension the rope can stand before breaking is given by  . Which of the following represents the ball's linear velocity given that the rope does not break?
. Which of the following represents the ball's linear velocity given that the rope does not break?

A ball of mass 


This is a centripetal force problem. In this case the tension on the rope is the centripetal force that keeps the ball moving on a circle.
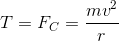
If we want for the rope not to break, then the tension should never exceed  .
.

Now we just solve for velocity:

This is a centripetal force problem. In this case the tension on the rope is the centripetal force that keeps the ball moving on a circle.
If we want for the rope not to break, then the tension should never exceed 
Now we just solve for velocity:
Compare your answer with the correct one above

A ball of mass  is tied to a rope and moves along a horizontal circular path of radius
is tied to a rope and moves along a horizontal circular path of radius  as shown in the diagram (view from above). The maximum tension the rope can stand before breaking is given by
as shown in the diagram (view from above). The maximum tension the rope can stand before breaking is given by  . Which of the following represents the ball's linear velocity given that the rope does not break?
. Which of the following represents the ball's linear velocity given that the rope does not break?

A ball of mass 


This is a centripetal force problem. In this case the tension on the rope is the centripetal force that keeps the ball moving on a circle.
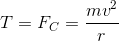
If we want for the rope not to break, then the tension should never exceed  .
.

Now we just solve for velocity:

This is a centripetal force problem. In this case the tension on the rope is the centripetal force that keeps the ball moving on a circle.
If we want for the rope not to break, then the tension should never exceed 
Now we just solve for velocity:
Compare your answer with the correct one above