Mechanics Exam - AP Physics C Electricity & Magnetism
Card 0 of 20
With what minimum velocity must a rocket be launched from the surface of the moon in order to not fall back down due to the moon's gravity?
The mass of the moon is  and its radius is
and its radius is  .
.

With what minimum velocity must a rocket be launched from the surface of the moon in order to not fall back down due to the moon's gravity?
The mass of the moon is 

Relevant equations:



For the rocket to escape the moon's gravity, its minimum total energy is zero. If the total energy is zero, the rocket will have zero final velocity when it is infinitely far from the moon. If total energy is less than zero, the rocket will fall back to the moon's surface. If total energy is greater than zero, the rocket will have some final velocity when it is infinitely far away.
For the minimum energy case as the rocket leaves the surface:

Rearrange energy equation to isolate the velocity term.


Substitute in the given values to solve for the velocity.

Relevant equations:
For the rocket to escape the moon's gravity, its minimum total energy is zero. If the total energy is zero, the rocket will have zero final velocity when it is infinitely far from the moon. If total energy is less than zero, the rocket will fall back to the moon's surface. If total energy is greater than zero, the rocket will have some final velocity when it is infinitely far away.
For the minimum energy case as the rocket leaves the surface:
Rearrange energy equation to isolate the velocity term.
Substitute in the given values to solve for the velocity.
Compare your answer with the correct one above
What is the gravitational force of the sun on a  book on the earth's surface if the sun's mass is
book on the earth's surface if the sun's mass is  and the earth-sun distance is
and the earth-sun distance is  ?
?

What is the gravitational force of the sun on a 


Relevant equations:

Use the given values to solve for the force.

Relevant equations:
Use the given values to solve for the force.
Compare your answer with the correct one above
Two spheres of equal mass are isolated in space, and are separated by a distance  . If that distance is doubled, by what factor does the gravitational force between the two spheres change?
. If that distance is doubled, by what factor does the gravitational force between the two spheres change?
Two spheres of equal mass are isolated in space, and are separated by a distance 
Newton's law of universal gravitation states:

We can write two equations for the gravity experienced before and after the doubling:


The equation for gravity after the doubling can be simplified:


Because the masses of the spheres remain the same, as does the universal gravitation constant, we can substitute the definition of Fg1 into that equation:

The the gravitational force decreases by a factor of 4 when the distance between the two spheres is doubled.
Newton's law of universal gravitation states:
We can write two equations for the gravity experienced before and after the doubling:
The equation for gravity after the doubling can be simplified:
Because the masses of the spheres remain the same, as does the universal gravitation constant, we can substitute the definition of Fg1 into that equation:
The the gravitational force decreases by a factor of 4 when the distance between the two spheres is doubled.
Compare your answer with the correct one above
Two spheres of equal mass are isolated in space. If the mass of one sphere is doubled, by what factor does the gravitational force experienced by the two spheres change?
Two spheres of equal mass are isolated in space. If the mass of one sphere is doubled, by what factor does the gravitational force experienced by the two spheres change?
Newton's law of universal gravitation states that:

We can write two equations representing the force of gravity before and after the doubling of the mass:


The problem gives us  and we can assume that all other variables stay constant.
and we can assume that all other variables stay constant.
Substituting these defintions into the second equation:

This equation simplifies to:

Substituting the definition of Fg1, we see:

Thus the gravitational forces doubles when the mass of one object doubles.
Newton's law of universal gravitation states that:
We can write two equations representing the force of gravity before and after the doubling of the mass:
The problem gives us 
Substituting these defintions into the second equation:
This equation simplifies to:
Substituting the definition of Fg1, we see:
Thus the gravitational forces doubles when the mass of one object doubles.
Compare your answer with the correct one above
You are riding in an elevator that is accelerating upwards at  , when you note that a block suspended vertically from a spring scale gives a reading of
, when you note that a block suspended vertically from a spring scale gives a reading of  .
.
What does the spring scale read when the elevator is descending at constant speed?
You are riding in an elevator that is accelerating upwards at 

What does the spring scale read when the elevator is descending at constant speed?
When the elevator accelerates upward, we know that an object would appear heavier. The normal force is the sum of all the forces added up, and in this case it is  . We know that the normal force has two components, a component from gravity, and a component from the acceleration of the elevator. Using this equation, we can determine the mass of the block, which doesn't change:
. We know that the normal force has two components, a component from gravity, and a component from the acceleration of the elevator. Using this equation, we can determine the mass of the block, which doesn't change:

 is acceleration due to gravity and
is acceleration due to gravity and  is the acceleration of the elevator.
is the acceleration of the elevator.
When substituting in the values, we get 
Solving for  , we get
, we get 
Since the elevator is descending at constant speed, no additional force is applied, therefore the force that the spring scale reads is only due to gravity, which is calculated by:


When the elevator accelerates upward, we know that an object would appear heavier. The normal force is the sum of all the forces added up, and in this case it is 


When substituting in the values, we get
Solving for 
Since the elevator is descending at constant speed, no additional force is applied, therefore the force that the spring scale reads is only due to gravity, which is calculated by:
Compare your answer with the correct one above
The mass and radius of a planet’s moon are  and
and  respectively.
respectively.
With what minimum speed would a bullet have to be fired horizontally near the surface of this moon in order for it to never hit the ground?
(Note: You can treat the moon as a smooth sphere, and assume there’s no atmosphere.)
The mass and radius of a planet’s moon are 

With what minimum speed would a bullet have to be fired horizontally near the surface of this moon in order for it to never hit the ground?
(Note: You can treat the moon as a smooth sphere, and assume there’s no atmosphere.)
To do this problem we have to realize that the force of gravity acting on the bullet is equal to the centripetal force. The equations for gravitational force and centripetal force are as follows:

If we set the two equations equal to each other, the small  (mass of the bullet) will cancel out and
(mass of the bullet) will cancel out and  will disappear from the right side of the equation.
will disappear from the right side of the equation.

 is the universal gravitational constant
is the universal gravitational constant 
 is given to be
is given to be  and
and  to be
to be  .
.
If we plug everything in, we get
 or
or 
To do this problem we have to realize that the force of gravity acting on the bullet is equal to the centripetal force. The equations for gravitational force and centripetal force are as follows:
If we set the two equations equal to each other, the small 






If we plug everything in, we get

Compare your answer with the correct one above
With what minimum velocity must a rocket be launched from the surface of the moon in order to not fall back down due to the moon's gravity?
The mass of the moon is  and its radius is
and its radius is  .
.

With what minimum velocity must a rocket be launched from the surface of the moon in order to not fall back down due to the moon's gravity?
The mass of the moon is 

Relevant equations:



For the rocket to escape the moon's gravity, its minimum total energy is zero. If the total energy is zero, the rocket will have zero final velocity when it is infinitely far from the moon. If total energy is less than zero, the rocket will fall back to the moon's surface. If total energy is greater than zero, the rocket will have some final velocity when it is infinitely far away.
For the minimum energy case as the rocket leaves the surface:

Rearrange energy equation to isolate the velocity term.


Substitute in the given values to solve for the velocity.

Relevant equations:
For the rocket to escape the moon's gravity, its minimum total energy is zero. If the total energy is zero, the rocket will have zero final velocity when it is infinitely far from the moon. If total energy is less than zero, the rocket will fall back to the moon's surface. If total energy is greater than zero, the rocket will have some final velocity when it is infinitely far away.
For the minimum energy case as the rocket leaves the surface:
Rearrange energy equation to isolate the velocity term.
Substitute in the given values to solve for the velocity.
Compare your answer with the correct one above
What is the gravitational force of the sun on a  book on the earth's surface if the sun's mass is
book on the earth's surface if the sun's mass is  and the earth-sun distance is
and the earth-sun distance is  ?
?

What is the gravitational force of the sun on a 


Relevant equations:

Use the given values to solve for the force.

Relevant equations:
Use the given values to solve for the force.
Compare your answer with the correct one above
Two spheres of equal mass are isolated in space, and are separated by a distance  . If that distance is doubled, by what factor does the gravitational force between the two spheres change?
. If that distance is doubled, by what factor does the gravitational force between the two spheres change?
Two spheres of equal mass are isolated in space, and are separated by a distance 
Newton's law of universal gravitation states:

We can write two equations for the gravity experienced before and after the doubling:


The equation for gravity after the doubling can be simplified:


Because the masses of the spheres remain the same, as does the universal gravitation constant, we can substitute the definition of Fg1 into that equation:

The the gravitational force decreases by a factor of 4 when the distance between the two spheres is doubled.
Newton's law of universal gravitation states:
We can write two equations for the gravity experienced before and after the doubling:
The equation for gravity after the doubling can be simplified:
Because the masses of the spheres remain the same, as does the universal gravitation constant, we can substitute the definition of Fg1 into that equation:
The the gravitational force decreases by a factor of 4 when the distance between the two spheres is doubled.
Compare your answer with the correct one above
Two spheres of equal mass are isolated in space. If the mass of one sphere is doubled, by what factor does the gravitational force experienced by the two spheres change?
Two spheres of equal mass are isolated in space. If the mass of one sphere is doubled, by what factor does the gravitational force experienced by the two spheres change?
Newton's law of universal gravitation states that:

We can write two equations representing the force of gravity before and after the doubling of the mass:


The problem gives us  and we can assume that all other variables stay constant.
and we can assume that all other variables stay constant.
Substituting these defintions into the second equation:

This equation simplifies to:

Substituting the definition of Fg1, we see:

Thus the gravitational forces doubles when the mass of one object doubles.
Newton's law of universal gravitation states that:
We can write two equations representing the force of gravity before and after the doubling of the mass:
The problem gives us 
Substituting these defintions into the second equation:
This equation simplifies to:
Substituting the definition of Fg1, we see:
Thus the gravitational forces doubles when the mass of one object doubles.
Compare your answer with the correct one above
You are riding in an elevator that is accelerating upwards at  , when you note that a block suspended vertically from a spring scale gives a reading of
, when you note that a block suspended vertically from a spring scale gives a reading of  .
.
What does the spring scale read when the elevator is descending at constant speed?
You are riding in an elevator that is accelerating upwards at 

What does the spring scale read when the elevator is descending at constant speed?
When the elevator accelerates upward, we know that an object would appear heavier. The normal force is the sum of all the forces added up, and in this case it is  . We know that the normal force has two components, a component from gravity, and a component from the acceleration of the elevator. Using this equation, we can determine the mass of the block, which doesn't change:
. We know that the normal force has two components, a component from gravity, and a component from the acceleration of the elevator. Using this equation, we can determine the mass of the block, which doesn't change:

 is acceleration due to gravity and
is acceleration due to gravity and  is the acceleration of the elevator.
is the acceleration of the elevator.
When substituting in the values, we get 
Solving for  , we get
, we get 
Since the elevator is descending at constant speed, no additional force is applied, therefore the force that the spring scale reads is only due to gravity, which is calculated by:


When the elevator accelerates upward, we know that an object would appear heavier. The normal force is the sum of all the forces added up, and in this case it is 


When substituting in the values, we get
Solving for 
Since the elevator is descending at constant speed, no additional force is applied, therefore the force that the spring scale reads is only due to gravity, which is calculated by:
Compare your answer with the correct one above
The mass and radius of a planet’s moon are  and
and  respectively.
respectively.
With what minimum speed would a bullet have to be fired horizontally near the surface of this moon in order for it to never hit the ground?
(Note: You can treat the moon as a smooth sphere, and assume there’s no atmosphere.)
The mass and radius of a planet’s moon are 

With what minimum speed would a bullet have to be fired horizontally near the surface of this moon in order for it to never hit the ground?
(Note: You can treat the moon as a smooth sphere, and assume there’s no atmosphere.)
To do this problem we have to realize that the force of gravity acting on the bullet is equal to the centripetal force. The equations for gravitational force and centripetal force are as follows:

If we set the two equations equal to each other, the small  (mass of the bullet) will cancel out and
(mass of the bullet) will cancel out and  will disappear from the right side of the equation.
will disappear from the right side of the equation.

 is the universal gravitational constant
is the universal gravitational constant 
 is given to be
is given to be  and
and  to be
to be  .
.
If we plug everything in, we get
 or
or 
To do this problem we have to realize that the force of gravity acting on the bullet is equal to the centripetal force. The equations for gravitational force and centripetal force are as follows:
If we set the two equations equal to each other, the small 






If we plug everything in, we get

Compare your answer with the correct one above
A man runs with a velocity described by the function below.

What is the function for his acceleration?
A man runs with a velocity described by the function below.
What is the function for his acceleration?
The function for acceleration is the derivative of the function for velocity.



The function for acceleration is the derivative of the function for velocity.
Compare your answer with the correct one above
A man runs with a velocity as described by the function below.

How far does he travel in 1 minute?
A man runs with a velocity as described by the function below.
How far does he travel in 1 minute?
Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.



Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.
Compare your answer with the correct one above
A particle traveling in a straight line accelerates uniformly from rest to  in
in  and then continues at constant speed for an additional for an additional
and then continues at constant speed for an additional for an additional  . What is the total distance traveled by the particle during the
. What is the total distance traveled by the particle during the  ?
?
A particle traveling in a straight line accelerates uniformly from rest to 



First off we have to convert  to meters per second.
to meters per second.

Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be  . The acceleration of the object at this time can be calculated using:
. The acceleration of the object at this time can be calculated using:
 , substituting the values, we get:
, substituting the values, we get:

Next, we use the distance equation to find the distance in the first 5 seconds:

 because the initial speed is
because the initial speed is  .
.
If we plug in  ,
,  , we get:
, we get: 
Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:

 in this case is not equal to
in this case is not equal to  , it is equal to
, it is equal to  and
and 
Plugging in the equation, we get 
Adding  and
and  we get the total distance to be
we get the total distance to be 
First off we have to convert 
Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be 

Next, we use the distance equation to find the distance in the first 5 seconds:


If we plug in 

Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:



Plugging in the equation, we get
Adding 

Compare your answer with the correct one above
A man runs with a velocity described by the function below.

What is the function for his acceleration?
A man runs with a velocity described by the function below.
What is the function for his acceleration?
The function for acceleration is the derivative of the function for velocity.



The function for acceleration is the derivative of the function for velocity.
Compare your answer with the correct one above
A man runs with a velocity as described by the function below.

How far does he travel in 1 minute?
A man runs with a velocity as described by the function below.
How far does he travel in 1 minute?
Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.



Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.
Compare your answer with the correct one above
A particle traveling in a straight line accelerates uniformly from rest to  in
in  and then continues at constant speed for an additional for an additional
and then continues at constant speed for an additional for an additional  . What is the total distance traveled by the particle during the
. What is the total distance traveled by the particle during the  ?
?
A particle traveling in a straight line accelerates uniformly from rest to 



First off we have to convert  to meters per second.
to meters per second.

Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be  . The acceleration of the object at this time can be calculated using:
. The acceleration of the object at this time can be calculated using:
 , substituting the values, we get:
, substituting the values, we get:

Next, we use the distance equation to find the distance in the first 5 seconds:

 because the initial speed is
because the initial speed is  .
.
If we plug in  ,
,  , we get:
, we get: 
Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:

 in this case is not equal to
in this case is not equal to  , it is equal to
, it is equal to  and
and 
Plugging in the equation, we get 
Adding  and
and  we get the total distance to be
we get the total distance to be 
First off we have to convert 
Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be 

Next, we use the distance equation to find the distance in the first 5 seconds:


If we plug in 

Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:



Plugging in the equation, we get
Adding 

Compare your answer with the correct one above
A  ball is thrown horizontally from the top of a
ball is thrown horizontally from the top of a 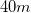 high building. It has an initial velocity of
high building. It has an initial velocity of 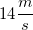 and lands on the ground
and lands on the ground  away from the base of the building. Assuming air resistance is negligible, which of the following changes would cause the range of this projectile to increase?
away from the base of the building. Assuming air resistance is negligible, which of the following changes would cause the range of this projectile to increase?
I. Increasing the initial horizontal velocity
II. Decreasing the mass of the ball
III. Throwing the ball from an identical building on the moon
A 
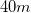
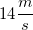

I. Increasing the initial horizontal velocity
II. Decreasing the mass of the ball
III. Throwing the ball from an identical building on the moon
Relevant equations:


Choice I is true because  is proportional to the range
is proportional to the range  , so increasing
, so increasing  increases
increases  if
if  is constant. This relationship is given by the equation:
is constant. This relationship is given by the equation:

Choice II is false because the motion of a projectile is independent of mass.
Choice III is true because the vertical acceleration on the moon  would be less. Decreasing
would be less. Decreasing 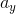 increases the time the ball is in the air, thereby increasing
increases the time the ball is in the air, thereby increasing  if
if  is constant. This relationship is also shown in the equation:
is constant. This relationship is also shown in the equation:

Relevant equations:
Choice I is true because 




Choice II is false because the motion of a projectile is independent of mass.
Choice III is true because the vertical acceleration on the moon 


Compare your answer with the correct one above
Water emerges horizontally from a hole in a tank 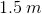 above the ground. If the water hits the ground
above the ground. If the water hits the ground 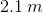 from the base of the tank, at what speed is the water emerging from the hole? (Hint: Treat the water droplets as projectiles.)
from the base of the tank, at what speed is the water emerging from the hole? (Hint: Treat the water droplets as projectiles.)
Water emerges horizontally from a hole in a tank 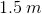
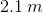
To understand this problem, we have to understand that the water has a x-velocity and a y-veloctiy. The x-velocity never changes.
First we want to find the time it took for the water to hit the ground. We can use this equation: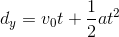
We know that the y-velocity is 0 to start with, acceleration is  and
and  .
.
Substituting into the equation, we get:

Next we have to substitute the time into the equation for the x component

We know that  and
and 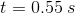 , so we can conclude that:
, so we can conclude that:
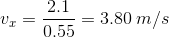
To understand this problem, we have to understand that the water has a x-velocity and a y-veloctiy. The x-velocity never changes.
First we want to find the time it took for the water to hit the ground. We can use this equation:
We know that the y-velocity is 0 to start with, acceleration is 

Substituting into the equation, we get:
Next we have to substitute the time into the equation for the x component
We know that 
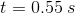
Compare your answer with the correct one above