Magnetism - AP Physics C Electricity & Magnetism

Card 0 of 20

Question

An infinitely long wire has a current of running through it. Calculate the magnetic field at a distance away from the wire.

$\mu_0=4\pi *10^{-7}\frac{Tm}{A}$

Answer

For infinitely long wires, the formula for the magnetic field is $B=\frac{\mu_0I}{2\pi r}$ , where is the current and is the distance from the wire.

The magnetic field is calculated using our given values.

$B=\frac{(4\pi10^{-7}\frac{\text{Tm}}{\text{A}})(3\text{A})}{2\pi(0.02\text{m})}$

$B=310^{-5}\ \text{T}$

Compare your answer with the correct one above

Question

A solenoid is long and it is made up of turns of wire. How much current must run through the solenoid to generate a magnetic field of inside of the solenoid?

$\mu_0=4\pi*10^{-7}\frac{Tm}{A}$

Answer

The formula for the magnetic field inside the solenoid is $B=\frac{N}{L}\mu_0I$ , where is the number of turns of wire, is the length of the solenoid, and is the current.

We want to find the current so we solve for .

$I=\frac{BL}{N\mu_0}$

Plug in the values.

$I=\frac{(1\text{T})(0.5\text{m})}{(800)(4\pi*10^{-7}\frac{\text{Tm}}{\text{A}{}})}$

$I=497\ \text{A}$

Compare your answer with the correct one above

Question

Two parallel wires a distance apart each carry a current , and repel each other with a force per unit length. If the current in each wire is doubled to , and the distance between them is halved to $\frac{R}{2}$ , by what factor does the force per unit length change?

Answer

Relevant equations:

$\oint B\cdot dl = \mu _o I$

$F = I L \times B$

Step 1: Find the original and new magnetic fields created by wire 1 at wire 2, using Ampere's law with an Amperian loop of radius or $\frac{R}{2}$ , respectively.

Original

$B (2\pi R) = \mu _o I \rightarrow B = \frac{\mu _o I}{2 \pi R}$

New

$B (2\pi (\frac{R}{2})) = \mu _o (2I) \rightarrow B = \frac{\mu _o (2I)}{2\pi \frac{R}{2}} = \frac{4\mu _o I}{2\pi R}$

Since the wires are parallel to each other and wire 1's field is directed circularly around it, in each case wire 1's field is perpendicular to wire 2.

Step 2: Find the original and new magnetic forces per unit length on wire 2, due to the field created by wire 1.

$F = IL \times B \rightarrow \frac{F}{L} = IB$

Original

$\frac{F}{L} = I * \frac{\mu _o I }{2 \pi R} = \frac{\mu _o I^2}{2\pi R}\textup{}$

New

$\frac{F}{L} = 2I * \frac{4\mu _o I}{2\pi R} = \frac{8 \mu _o I^2}{2 \pi R}$

So, the new force per unit length is 8 times greater than the original.

Compare your answer with the correct one above

Question

A region of uniform magnetic field, , is represented by the grey area of the box in the diagram. The magnetic field is oriented into the page.

A stream of protons moving at velocity $\vec{v}$ is directed into the region of the magnetic field, as shown. Identify the correct path of the stream of protons after they enter the region of magnetic field.

Answer

The magnetic force on a moving charged particle is given by the equation:

$\vec{F}=q,\vec{v}\times \vec{B}$

Isolating the directional component of this equation yields the understanding that the resulting force on a moving charged particle is perpendicular to the plane of the velocity vector and magnetic field vector. Using the right-hand-rule on this cross-product shows that the velocity vector right-crossed into the magnetic field vector into the page yields a magnetic force vector upward on a positive charge. This will result in a semi-circular path oriented vertically upward.

Compare your answer with the correct one above

Question

An infinitely long wire has a current of running through it. Calculate the magnetic field at a distance away from the wire.

$\mu_0=4\pi *10^{-7}\frac{Tm}{A}$

Answer

For infinitely long wires, the formula for the magnetic field is $B=\frac{\mu_0I}{2\pi r}$ , where is the current and is the distance from the wire.

The magnetic field is calculated using our given values.

$B=\frac{(4\pi10^{-7}\frac{\text{Tm}}{\text{A}})(3\text{A})}{2\pi(0.02\text{m})}$

$B=310^{-5}\ \text{T}$

Compare your answer with the correct one above

Question

A solenoid is long and it is made up of turns of wire. How much current must run through the solenoid to generate a magnetic field of inside of the solenoid?

$\mu_0=4\pi*10^{-7}\frac{Tm}{A}$

Answer

The formula for the magnetic field inside the solenoid is $B=\frac{N}{L}\mu_0I$ , where is the number of turns of wire, is the length of the solenoid, and is the current.

We want to find the current so we solve for .

$I=\frac{BL}{N\mu_0}$

Plug in the values.

$I=\frac{(1\text{T})(0.5\text{m})}{(800)(4\pi*10^{-7}\frac{\text{Tm}}{\text{A}{}})}$

$I=497\ \text{A}$

Compare your answer with the correct one above

Question

Two parallel wires a distance apart each carry a current , and repel each other with a force per unit length. If the current in each wire is doubled to , and the distance between them is halved to $\frac{R}{2}$ , by what factor does the force per unit length change?

Answer

Relevant equations:

$\oint B\cdot dl = \mu _o I$

$F = I L \times B$

Step 1: Find the original and new magnetic fields created by wire 1 at wire 2, using Ampere's law with an Amperian loop of radius or $\frac{R}{2}$ , respectively.

Original

$B (2\pi R) = \mu _o I \rightarrow B = \frac{\mu _o I}{2 \pi R}$

New

$B (2\pi (\frac{R}{2})) = \mu _o (2I) \rightarrow B = \frac{\mu _o (2I)}{2\pi \frac{R}{2}} = \frac{4\mu _o I}{2\pi R}$

Since the wires are parallel to each other and wire 1's field is directed circularly around it, in each case wire 1's field is perpendicular to wire 2.

Step 2: Find the original and new magnetic forces per unit length on wire 2, due to the field created by wire 1.

$F = IL \times B \rightarrow \frac{F}{L} = IB$

Original

$\frac{F}{L} = I * \frac{\mu _o I }{2 \pi R} = \frac{\mu _o I^2}{2\pi R}\textup{}$

New

$\frac{F}{L} = 2I * \frac{4\mu _o I}{2\pi R} = \frac{8 \mu _o I^2}{2 \pi R}$

So, the new force per unit length is 8 times greater than the original.

Compare your answer with the correct one above

Question

A region of uniform magnetic field, , is represented by the grey area of the box in the diagram. The magnetic field is oriented into the page.

A stream of protons moving at velocity $\vec{v}$ is directed into the region of the magnetic field, as shown. Identify the correct path of the stream of protons after they enter the region of magnetic field.

Answer

The magnetic force on a moving charged particle is given by the equation:

$\vec{F}=q,\vec{v}\times \vec{B}$

Isolating the directional component of this equation yields the understanding that the resulting force on a moving charged particle is perpendicular to the plane of the velocity vector and magnetic field vector. Using the right-hand-rule on this cross-product shows that the velocity vector right-crossed into the magnetic field vector into the page yields a magnetic force vector upward on a positive charge. This will result in a semi-circular path oriented vertically upward.

Compare your answer with the correct one above

Question

A proton traveling $600\frac{m}{s}$ enters a uniform magnetic field and experiences a magnetic force, causing it to travel in a circular path. Taking the magnetic field to be , what is the radius of this circular path (shown in red)?

$m_{proton}=1.6710^{-27}\ \text{kg}$

$q_{proton}=1.610^{-19}\ \text{C}$

Answer

To calculate the magnetic force of a single charge, we use , where is the charge of the proton, is its velocity, is the uniform magnetic field.

Since this magnetic force causes the proton to travel in a circular path, we set this magnetic force equation equal to the centripetal force equation.

$qvB=\frac{mv^2}{r}$

is the mass of the proton and is the radius of the circular path. Solve for .

$r=\frac{mv}{qB}$

Using the values given in the question, we can solve for the radius.

$r=\frac{(1.6710^{-27}kg)(600\frac{m}{s})}{(1.610^{-19}C)(0.0002T)}$

$r=0.031\ \text{m}=3.1\ \text{cm}$

Compare your answer with the correct one above

Question

Which of the following best describes the net magnetic flux through a closed sphere, in the presence of a magnet?

Answer

The net magnetic flux (or net field flowing in and out) through any closed surface must always be zero. This is because magnetic field lines have no starting or ending points, so any field line going into the surface must also come out. In other words, "there are no magnetic monopoles."

Compare your answer with the correct one above

Question

A particle of charge and mass moves with a speed of perpendicular to a uniform magnetic field, . What is the period of the particle's orbit in the field?

Answer

Relevant equations:

$F_m = qv \times B$

$F_c = \frac{mv^2}{r}$

Set the magnetic force equal to the centripetal force, since the magnetic force is directed towards the center of the particle's circular path and centripetal force is defined as the net force towards the center of a circular path.

$qvB = \frac{mv^2}{r}$

Rearrange to isolate the velocity:

$v = \frac{qBr}{m}$

Determine the distance, , traveled in one revolution, which is the circumference of a circle of radius :

$D = 2\pi r$

Plug this distance and velocity into , to solve for the period :

$D = v * T \rightarrow T = \frac{D}{v} = \frac{m}{qBr} * \frac{2\pi r}{1} = \frac{2\pi m}{qB}$

Compare your answer with the correct one above

Question

Consider a current-carrying loop with current , radius , and center .

A particle with charge flies through the center and into the page with velocity . What is the total electromagnetic force on the particle at the instant that it flies through the loop, in terms of the variables given?

Answer

The correct answer is zero. To calculate the force of a magnetic field on a moving charged particle, we use the cross product. We know that if the magnetic field is parallel to the velocity vector of the particle, then the force produced is zero.

$\vec F=Q\vec v\times \vec B$

Because our magnetic field in this case is going in the same direction as the velocity of the particle, we know that the magnetic force on the particle is zero.

Compare your answer with the correct one above

Question

Consider two long, straight, current-carrying wires at distance from each other, each with a current of magnitude going in opposite directions.

If the two wires described are not held in place, what motion will result from the magnetic fields produced?

Answer

The answer is that the wires will move from each other. Using our right hand rule, we know that the magnetic fields produced by each wire are in the same direction, as long as their currents oppose. Using the right hand rule again to determine the direction of the force exerted on each wire by the magnetic field with which they are interacting yields a force in the direction away from the other wire for each wire.

Compare your answer with the correct one above

Question

A proton traveling $600\frac{m}{s}$ enters a uniform magnetic field and experiences a magnetic force, causing it to travel in a circular path. Taking the magnetic field to be , what is the radius of this circular path (shown in red)?

$m_{proton}=1.6710^{-27}\ \text{kg}$

$q_{proton}=1.610^{-19}\ \text{C}$

Answer

To calculate the magnetic force of a single charge, we use , where is the charge of the proton, is its velocity, is the uniform magnetic field.

Since this magnetic force causes the proton to travel in a circular path, we set this magnetic force equation equal to the centripetal force equation.

$qvB=\frac{mv^2}{r}$

is the mass of the proton and is the radius of the circular path. Solve for .

$r=\frac{mv}{qB}$

Using the values given in the question, we can solve for the radius.

$r=\frac{(1.6710^{-27}kg)(600\frac{m}{s})}{(1.610^{-19}C)(0.0002T)}$

$r=0.031\ \text{m}=3.1\ \text{cm}$

Compare your answer with the correct one above

Question

Which of the following best describes the net magnetic flux through a closed sphere, in the presence of a magnet?

Answer

The net magnetic flux (or net field flowing in and out) through any closed surface must always be zero. This is because magnetic field lines have no starting or ending points, so any field line going into the surface must also come out. In other words, "there are no magnetic monopoles."

Compare your answer with the correct one above

Question

A particle of charge and mass moves with a speed of perpendicular to a uniform magnetic field, . What is the period of the particle's orbit in the field?

Answer

Relevant equations:

$F_m = qv \times B$

$F_c = \frac{mv^2}{r}$

Set the magnetic force equal to the centripetal force, since the magnetic force is directed towards the center of the particle's circular path and centripetal force is defined as the net force towards the center of a circular path.

$qvB = \frac{mv^2}{r}$

Rearrange to isolate the velocity:

$v = \frac{qBr}{m}$

Determine the distance, , traveled in one revolution, which is the circumference of a circle of radius :

$D = 2\pi r$

Plug this distance and velocity into , to solve for the period :

$D = v * T \rightarrow T = \frac{D}{v} = \frac{m}{qBr} * \frac{2\pi r}{1} = \frac{2\pi m}{qB}$

Compare your answer with the correct one above

Question

Consider a current-carrying loop with current , radius , and center .

A particle with charge flies through the center and into the page with velocity . What is the total electromagnetic force on the particle at the instant that it flies through the loop, in terms of the variables given?

Answer

The correct answer is zero. To calculate the force of a magnetic field on a moving charged particle, we use the cross product. We know that if the magnetic field is parallel to the velocity vector of the particle, then the force produced is zero.

$\vec F=Q\vec v\times \vec B$

Because our magnetic field in this case is going in the same direction as the velocity of the particle, we know that the magnetic force on the particle is zero.

Compare your answer with the correct one above

Question

Consider two long, straight, current-carrying wires at distance from each other, each with a current of magnitude going in opposite directions.

If the two wires described are not held in place, what motion will result from the magnetic fields produced?

Answer

The answer is that the wires will move from each other. Using our right hand rule, we know that the magnetic fields produced by each wire are in the same direction, as long as their currents oppose. Using the right hand rule again to determine the direction of the force exerted on each wire by the magnetic field with which they are interacting yields a force in the direction away from the other wire for each wire.

Compare your answer with the correct one above

Question

Two infinitely long wires having currents and are separated by a distance .

The current is 6A into the page. The current is 9A into the page. The distance of separation is 1.5mm. The point lies 1.5mm away from on a line connecting the centers of the two wires.

What is the magnitude and direction of the net magnetic field at the point ?

$\mu_0=4\pi*10^{-7}\frac{T\cdot m}{A}$

Answer

At point , the magnetic field due to points right (via the right hand rule) with a magnitude given by:

$B_{1}=\left| \frac{\mu_{o} I_{1}}{2\pi r_{1}} \right|$

$B_{1}=\left| \frac{(4\pi10^{-7}\frac{T\cdot m}{A})(6A)}{2\pi (1.5mm)} \right|=810^{-4}T$

At point , the magnetic field due to points right (via the right hand rule) with a magnitude given by:

$B_{2}=\left| \frac{\mu_{o} I_{2}}{2\pi r_{2}} \right|$

$B_{2}=\left| \frac{(4\pi10^{-7}\frac{T\cdot m}{A})(9A)}{2\pi (3.0mm)} \right|=610^{-4}T$

The addition of these two vectors, both pointing in the same direction, results in a net magnetic field vector of magnitude $1.410^{-3}T$ to the right.

$810^{-4}T+610^{-4}T=1.410^{-3}T$

Compare your answer with the correct one above

Question

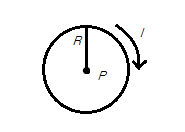
Consider a current-carrying loop with current , radius , and center .

What is the direction of the magnetic field produced?

Answer

The correct answer is into the page. As the current is moving clockwise, we can use our right hand rule for magnetic fields produced by a current-carrying loop. Curl the fingers of your right hand in the direction of the current. This should result in your thumb pointing toward the screen, indicating the direction of the magnetic field.

Compare your answer with the correct one above

Tap the card to reveal the answer