Electric Circuits - AP Physics C Electricity & Magnetism
Card 0 of 20
A straight copper wire has a fixed voltage applied across its length. Which of the following changes would increase the power dissipated by this wire?
A straight copper wire has a fixed voltage applied across its length. Which of the following changes would increase the power dissipated by this wire?
Relevant equations:



Current and resistance are inversely proportional to one another, assuming voltage is fixed. Since  , changes in current effect the power more than changes in resistance do. Thus, we need current to increase, meaning that resistance must decrease.
, changes in current effect the power more than changes in resistance do. Thus, we need current to increase, meaning that resistance must decrease.
To decrease resistance, we could:
1. Change the material of the wire to one of lesser resistivity
2. Decrease the length of the wire
3. Increase the cross-sectional area of the wire
4. Decrease the temperature of the wire (very slight effect on resistance)
Relevant equations:
Current and resistance are inversely proportional to one another, assuming voltage is fixed. Since 
To decrease resistance, we could:
1. Change the material of the wire to one of lesser resistivity
2. Decrease the length of the wire
3. Increase the cross-sectional area of the wire
4. Decrease the temperature of the wire (very slight effect on resistance)
Compare your answer with the correct one above
A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.
If the current through the wire is measured to be 2A, how much thermal energy is being lost per second as soon as the wire is connected to the battery?
A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.
If the current through the wire is measured to be 2A, how much thermal energy is being lost per second as soon as the wire is connected to the battery?
First, we must know that the wire has some internal resistance  . To calculate this, we need to know the potential drop through the wire, which must be the difference we saw from the initial voltage reading to the second. This value, 0.1V, we plug into Ohm's law to calculate the resistance of the wire.
. To calculate this, we need to know the potential drop through the wire, which must be the difference we saw from the initial voltage reading to the second. This value, 0.1V, we plug into Ohm's law to calculate the resistance of the wire.



The question asks for energy lost per second; this value is equivalent to the power.

Use our values to solve.

First, we must know that the wire has some internal resistance 
The question asks for energy lost per second; this value is equivalent to the power.
Use our values to solve.
Compare your answer with the correct one above
A simple circuit contains two  resistors in parallel, connected to a 20V source. What power is being provided by the source to the circuit?
resistors in parallel, connected to a 20V source. What power is being provided by the source to the circuit?
A simple circuit contains two 
The power supplied to the circuit can be calculated using the equation:

To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:



Now that we have the resistance and the voltage, we can solve for the power.

The power supplied to the circuit can be calculated using the equation:
To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:
Now that we have the resistance and the voltage, we can solve for the power.
Compare your answer with the correct one above
A straight copper wire has a fixed voltage applied across its length. Which of the following changes would increase the power dissipated by this wire?
A straight copper wire has a fixed voltage applied across its length. Which of the following changes would increase the power dissipated by this wire?
Relevant equations:



Current and resistance are inversely proportional to one another, assuming voltage is fixed. Since  , changes in current effect the power more than changes in resistance do. Thus, we need current to increase, meaning that resistance must decrease.
, changes in current effect the power more than changes in resistance do. Thus, we need current to increase, meaning that resistance must decrease.
To decrease resistance, we could:
1. Change the material of the wire to one of lesser resistivity
2. Decrease the length of the wire
3. Increase the cross-sectional area of the wire
4. Decrease the temperature of the wire (very slight effect on resistance)
Relevant equations:
Current and resistance are inversely proportional to one another, assuming voltage is fixed. Since 
To decrease resistance, we could:
1. Change the material of the wire to one of lesser resistivity
2. Decrease the length of the wire
3. Increase the cross-sectional area of the wire
4. Decrease the temperature of the wire (very slight effect on resistance)
Compare your answer with the correct one above
A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.
If the current through the wire is measured to be 2A, how much thermal energy is being lost per second as soon as the wire is connected to the battery?
A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.
If the current through the wire is measured to be 2A, how much thermal energy is being lost per second as soon as the wire is connected to the battery?
First, we must know that the wire has some internal resistance  . To calculate this, we need to know the potential drop through the wire, which must be the difference we saw from the initial voltage reading to the second. This value, 0.1V, we plug into Ohm's law to calculate the resistance of the wire.
. To calculate this, we need to know the potential drop through the wire, which must be the difference we saw from the initial voltage reading to the second. This value, 0.1V, we plug into Ohm's law to calculate the resistance of the wire.



The question asks for energy lost per second; this value is equivalent to the power.

Use our values to solve.

First, we must know that the wire has some internal resistance 
The question asks for energy lost per second; this value is equivalent to the power.
Use our values to solve.
Compare your answer with the correct one above
A simple circuit contains two  resistors in parallel, connected to a 20V source. What power is being provided by the source to the circuit?
resistors in parallel, connected to a 20V source. What power is being provided by the source to the circuit?
A simple circuit contains two 
The power supplied to the circuit can be calculated using the equation:

To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:



Now that we have the resistance and the voltage, we can solve for the power.

The power supplied to the circuit can be calculated using the equation:
To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:
Now that we have the resistance and the voltage, we can solve for the power.
Compare your answer with the correct one above
A lamp has a  bulb. If the house wiring provides
bulb. If the house wiring provides  to light up that bulb, how much current does the bulb draw?
to light up that bulb, how much current does the bulb draw?
A lamp has a 

The formula for power is , and we are given the following values.
and we are given the following values.


Solve for the current, 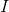 .
.

The formula for power is ,
Solve for the current, 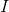
Compare your answer with the correct one above
A particle accelerator with a radius of 500 meters can have up to  protons circulating within it at once.
protons circulating within it at once.

How fast must the protons in the accelerator move in order to produce a current of 1A?
A particle accelerator with a radius of 500 meters can have up to 
How fast must the protons in the accelerator move in order to produce a current of 1A?
The current produced is the total charge that circulates the particle accelerator per unit time.
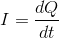
We calculate this by the equation:
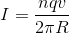
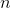 is the number of protons,
is the number of protons,  is the charge per proton,
is the charge per proton,  is the velocity of each proton, and
is the velocity of each proton, and  is the radius of the particle accelerator.
is the radius of the particle accelerator.
Using the given current, we then solve for the velocity:
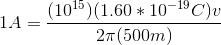

The current produced is the total charge that circulates the particle accelerator per unit time.
We calculate this by the equation:
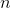



Using the given current, we then solve for the velocity:
Compare your answer with the correct one above
A lamp has a  bulb. If the house wiring provides
bulb. If the house wiring provides  to light up that bulb, how much current does the bulb draw?
to light up that bulb, how much current does the bulb draw?
A lamp has a 

The formula for power is , and we are given the following values.
and we are given the following values.


Solve for the current, 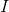 .
.

The formula for power is ,
Solve for the current, 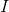
Compare your answer with the correct one above
A particle accelerator with a radius of 500 meters can have up to  protons circulating within it at once.
protons circulating within it at once.

How fast must the protons in the accelerator move in order to produce a current of 1A?
A particle accelerator with a radius of 500 meters can have up to 
How fast must the protons in the accelerator move in order to produce a current of 1A?
The current produced is the total charge that circulates the particle accelerator per unit time.
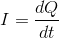
We calculate this by the equation:
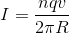
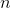 is the number of protons,
is the number of protons,  is the charge per proton,
is the charge per proton,  is the velocity of each proton, and
is the velocity of each proton, and  is the radius of the particle accelerator.
is the radius of the particle accelerator.
Using the given current, we then solve for the velocity:
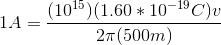

The current produced is the total charge that circulates the particle accelerator per unit time.
We calculate this by the equation:
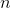



Using the given current, we then solve for the velocity:
Compare your answer with the correct one above
Three resistors and a battery form the following circuit.

Calculate the equivalent resistance if the resistors have the following values.



Three resistors and a battery form the following circuit.

Calculate the equivalent resistance if the resistors have the following values.
First, calculate the equivalent resistance of  and
and  . Since these two resistors are arranged in series, we just take the sum of their values.
. Since these two resistors are arranged in series, we just take the sum of their values.
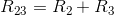


With resistors 2 and 3 combined together in a single value, the following circuit is formed.

Notice that  and
and  are arranged in parallel. To calculate the equivalent resistance of this parallel pair, we use the following equation.
are arranged in parallel. To calculate the equivalent resistance of this parallel pair, we use the following equation.

Plug in the values, and solve for 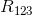 .
.


This is just like the circuit shown below.

First, calculate the equivalent resistance of 

With resistors 2 and 3 combined together in a single value, the following circuit is formed.

Notice that 

Plug in the values, and solve for 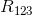
This is just like the circuit shown below.

Compare your answer with the correct one above
Three resistors and a battery form the following circuit.

Calculate the equivalent resistance if the resistors have the following values.



Three resistors and a battery form the following circuit.

Calculate the equivalent resistance if the resistors have the following values.
First, calculate the equivalent resistance of  and
and  . Since these two resistors are arranged in series, we just take the sum of their values.
. Since these two resistors are arranged in series, we just take the sum of their values.
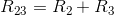


With resistors 2 and 3 combined together in a single value, the following circuit is formed.

Notice that  and
and  are arranged in parallel. To calculate the equivalent resistance of this parallel pair, we use the following equation.
are arranged in parallel. To calculate the equivalent resistance of this parallel pair, we use the following equation.

Plug in the values, and solve for 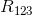 .
.


This is just like the circuit shown below.

First, calculate the equivalent resistance of 

With resistors 2 and 3 combined together in a single value, the following circuit is formed.

Notice that 

Plug in the values, and solve for 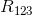
This is just like the circuit shown below.

Compare your answer with the correct one above
Three resistors R1, R2, and R3 and the capacitor, C, are connected to an ideal battery V to complete the circuit as shown.

After the circuit has been connected for a very long time, the currents in each branch of the circuit are measured to be some values  ,
,  , and
, and  , and the charge on the capacitor some value
, and the charge on the capacitor some value  .
.
Which of the following equations is a correct expression regarding the voltage of the circuit after a long time?
Three resistors R1, R2, and R3 and the capacitor, C, are connected to an ideal battery V to complete the circuit as shown.

After the circuit has been connected for a very long time, the currents in each branch of the circuit are measured to be some values 



Which of the following equations is a correct expression regarding the voltage of the circuit after a long time?
Identifying the sum of the voltage drops and rises (Kirchoff's Loop Law) around the three possible loops of this circuit is the key to answering this question correctly. The following signs can be assigned to each of the circuit elements based on the direction of the currents given.
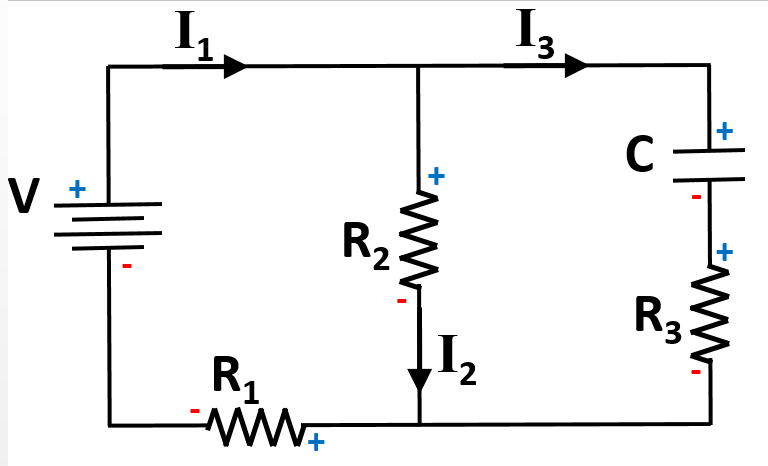
Use Ohm's law and the equation for capacitance to derive terms for the voltage across each element of the circuit.


There are three possible paths through the circuit, resulting in three correct equations that could be derived:



Only one of the given answer options matches up correctly to these.
Identifying the sum of the voltage drops and rises (Kirchoff's Loop Law) around the three possible loops of this circuit is the key to answering this question correctly. The following signs can be assigned to each of the circuit elements based on the direction of the currents given.

Use Ohm's law and the equation for capacitance to derive terms for the voltage across each element of the circuit.
There are three possible paths through the circuit, resulting in three correct equations that could be derived:
Only one of the given answer options matches up correctly to these.
Compare your answer with the correct one above
Three resistors R1, R2, and R3 and the capacitor, C, are connected to an ideal battery V to complete the circuit as shown.

After the circuit has been connected for a very long time, the currents in each branch of the circuit are measured to be some values  ,
,  , and
, and  , and the charge on the capacitor some value
, and the charge on the capacitor some value  .
.
Which of the following equations is a correct expression regarding the voltage of the circuit after a long time?
Three resistors R1, R2, and R3 and the capacitor, C, are connected to an ideal battery V to complete the circuit as shown.

After the circuit has been connected for a very long time, the currents in each branch of the circuit are measured to be some values 



Which of the following equations is a correct expression regarding the voltage of the circuit after a long time?
Identifying the sum of the voltage drops and rises (Kirchoff's Loop Law) around the three possible loops of this circuit is the key to answering this question correctly. The following signs can be assigned to each of the circuit elements based on the direction of the currents given.

Use Ohm's law and the equation for capacitance to derive terms for the voltage across each element of the circuit.


There are three possible paths through the circuit, resulting in three correct equations that could be derived:



Only one of the given answer options matches up correctly to these.
Identifying the sum of the voltage drops and rises (Kirchoff's Loop Law) around the three possible loops of this circuit is the key to answering this question correctly. The following signs can be assigned to each of the circuit elements based on the direction of the currents given.

Use Ohm's law and the equation for capacitance to derive terms for the voltage across each element of the circuit.
There are three possible paths through the circuit, resulting in three correct equations that could be derived:
Only one of the given answer options matches up correctly to these.
Compare your answer with the correct one above
A parallel plate capacitor has a capacitance of  . If the plates are
. If the plates are  apart, what is the area of the plates?
apart, what is the area of the plates?

A parallel plate capacitor has a capacitance of 

The relationship between capacitance, distance, and area is  . We can rearrange this equation to solve for area.
. We can rearrange this equation to solve for area.

Now, we can use the values given in teh question to solve.

The relationship between capacitance, distance, and area is 
Now, we can use the values given in teh question to solve.
Compare your answer with the correct one above
Charge is distributed uniformly over the area of the two plates of a parallel plate capacitor, resulting in a surface area charge density of  on the plates (the top plate is positive and the bottom is negative, as shown below). Each plate has area
on the plates (the top plate is positive and the bottom is negative, as shown below). Each plate has area  and are separated by distance
and are separated by distance  . A material of dielectric constant
. A material of dielectric constant  has been placed between the two plates.
has been placed between the two plates.

Which of the following would not result in an increase in the measure of electric potential difference between the two plates?
Charge is distributed uniformly over the area of the two plates of a parallel plate capacitor, resulting in a surface area charge density of 




Which of the following would not result in an increase in the measure of electric potential difference between the two plates?
The electric potential difference created between the plates of a parallel plate capactor is given by the equation:

The charge can be calculated by using the equation:

The value of the capacitance is related to the dimensions of the capacitor with the equation:

Combining these equations yields:

The area becomes inconsequential, while the potential is directly proportional to the surface charge density and the distance between the plates, and inversely proportional to the dielectric of the material between the plates. Changing the area does not cause any change in the potential difference measured between the plates, and changing any of the other variables would cause a resultant change in the potential difference.
The electric potential difference created between the plates of a parallel plate capactor is given by the equation:
The charge can be calculated by using the equation:
The value of the capacitance is related to the dimensions of the capacitor with the equation:
Combining these equations yields:
The area becomes inconsequential, while the potential is directly proportional to the surface charge density and the distance between the plates, and inversely proportional to the dielectric of the material between the plates. Changing the area does not cause any change in the potential difference measured between the plates, and changing any of the other variables would cause a resultant change in the potential difference.
Compare your answer with the correct one above
A parallel plate capacitor has a capacitance of  . If the plates are
. If the plates are  apart, what is the area of the plates?
apart, what is the area of the plates?

A parallel plate capacitor has a capacitance of 

The relationship between capacitance, distance, and area is  . We can rearrange this equation to solve for area.
. We can rearrange this equation to solve for area.

Now, we can use the values given in teh question to solve.

The relationship between capacitance, distance, and area is 
Now, we can use the values given in teh question to solve.
Compare your answer with the correct one above
Charge is distributed uniformly over the area of the two plates of a parallel plate capacitor, resulting in a surface area charge density of  on the plates (the top plate is positive and the bottom is negative, as shown below). Each plate has area
on the plates (the top plate is positive and the bottom is negative, as shown below). Each plate has area  and are separated by distance
and are separated by distance  . A material of dielectric constant
. A material of dielectric constant  has been placed between the two plates.
has been placed between the two plates.

Which of the following would not result in an increase in the measure of electric potential difference between the two plates?
Charge is distributed uniformly over the area of the two plates of a parallel plate capacitor, resulting in a surface area charge density of 




Which of the following would not result in an increase in the measure of electric potential difference between the two plates?
The electric potential difference created between the plates of a parallel plate capactor is given by the equation:

The charge can be calculated by using the equation:

The value of the capacitance is related to the dimensions of the capacitor with the equation:

Combining these equations yields:

The area becomes inconsequential, while the potential is directly proportional to the surface charge density and the distance between the plates, and inversely proportional to the dielectric of the material between the plates. Changing the area does not cause any change in the potential difference measured between the plates, and changing any of the other variables would cause a resultant change in the potential difference.
The electric potential difference created between the plates of a parallel plate capactor is given by the equation:
The charge can be calculated by using the equation:
The value of the capacitance is related to the dimensions of the capacitor with the equation:
Combining these equations yields:
The area becomes inconsequential, while the potential is directly proportional to the surface charge density and the distance between the plates, and inversely proportional to the dielectric of the material between the plates. Changing the area does not cause any change in the potential difference measured between the plates, and changing any of the other variables would cause a resultant change in the potential difference.
Compare your answer with the correct one above
Resistors are one of the most important basic components of a circuit. With very few exceptions, all circuits have at least one kind of resistor component. An ammeter is a device that measures current flowing through a circuit. Ammeters are always connected to a circuit in series.
Which of the following accurately explains why ammeters must be connected in series within a circuit, and never in parallel?
Resistors are one of the most important basic components of a circuit. With very few exceptions, all circuits have at least one kind of resistor component. An ammeter is a device that measures current flowing through a circuit. Ammeters are always connected to a circuit in series.
Which of the following accurately explains why ammeters must be connected in series within a circuit, and never in parallel?
In order to give accurate readings of current, ammeters have very low resistances. If connected in parallel, the voltage pushing current through the circuit would push a very strong current through the ammeter and virtually no current through the circuit's regular path. This would not only lead to a bad reading of current, but more often than not a broken ammeter. This phenomenon is an indication of why resistors are so important: they limit the current such that a circuit does not exceed its current-carrying capacity.
In order to give accurate readings of current, ammeters have very low resistances. If connected in parallel, the voltage pushing current through the circuit would push a very strong current through the ammeter and virtually no current through the circuit's regular path. This would not only lead to a bad reading of current, but more often than not a broken ammeter. This phenomenon is an indication of why resistors are so important: they limit the current such that a circuit does not exceed its current-carrying capacity.
Compare your answer with the correct one above
A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.
Why was the potential of the battery measured differently when the wire was connected?
A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.
Why was the potential of the battery measured differently when the wire was connected?
All wires have at least some internal resistance. The most likely explanation for this is that the wire is displaying slight resistance, and therefore caused the measured potential to be less than it was before.
All wires have at least some internal resistance. The most likely explanation for this is that the wire is displaying slight resistance, and therefore caused the measured potential to be less than it was before.
Compare your answer with the correct one above