AP Physics C - AP Physics C Electricity & Magnetism
Card 0 of 20
A straight copper wire has a fixed voltage applied across its length. Which of the following changes would increase the power dissipated by this wire?
A straight copper wire has a fixed voltage applied across its length. Which of the following changes would increase the power dissipated by this wire?
Relevant equations:



Current and resistance are inversely proportional to one another, assuming voltage is fixed. Since  , changes in current effect the power more than changes in resistance do. Thus, we need current to increase, meaning that resistance must decrease.
, changes in current effect the power more than changes in resistance do. Thus, we need current to increase, meaning that resistance must decrease.
To decrease resistance, we could:
1. Change the material of the wire to one of lesser resistivity
2. Decrease the length of the wire
3. Increase the cross-sectional area of the wire
4. Decrease the temperature of the wire (very slight effect on resistance)
Relevant equations:
Current and resistance are inversely proportional to one another, assuming voltage is fixed. Since 
To decrease resistance, we could:
1. Change the material of the wire to one of lesser resistivity
2. Decrease the length of the wire
3. Increase the cross-sectional area of the wire
4. Decrease the temperature of the wire (very slight effect on resistance)
Compare your answer with the correct one above
A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.
If the current through the wire is measured to be 2A, how much thermal energy is being lost per second as soon as the wire is connected to the battery?
A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.
If the current through the wire is measured to be 2A, how much thermal energy is being lost per second as soon as the wire is connected to the battery?
First, we must know that the wire has some internal resistance  . To calculate this, we need to know the potential drop through the wire, which must be the difference we saw from the initial voltage reading to the second. This value, 0.1V, we plug into Ohm's law to calculate the resistance of the wire.
. To calculate this, we need to know the potential drop through the wire, which must be the difference we saw from the initial voltage reading to the second. This value, 0.1V, we plug into Ohm's law to calculate the resistance of the wire.



The question asks for energy lost per second; this value is equivalent to the power.

Use our values to solve.

First, we must know that the wire has some internal resistance 
The question asks for energy lost per second; this value is equivalent to the power.
Use our values to solve.
Compare your answer with the correct one above
A simple circuit contains two  resistors in parallel, connected to a 20V source. What power is being provided by the source to the circuit?
resistors in parallel, connected to a 20V source. What power is being provided by the source to the circuit?
A simple circuit contains two 
The power supplied to the circuit can be calculated using the equation:

To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:



Now that we have the resistance and the voltage, we can solve for the power.

The power supplied to the circuit can be calculated using the equation:
To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:
Now that we have the resistance and the voltage, we can solve for the power.
Compare your answer with the correct one above
A straight copper wire has a fixed voltage applied across its length. Which of the following changes would increase the power dissipated by this wire?
A straight copper wire has a fixed voltage applied across its length. Which of the following changes would increase the power dissipated by this wire?
Relevant equations:



Current and resistance are inversely proportional to one another, assuming voltage is fixed. Since  , changes in current effect the power more than changes in resistance do. Thus, we need current to increase, meaning that resistance must decrease.
, changes in current effect the power more than changes in resistance do. Thus, we need current to increase, meaning that resistance must decrease.
To decrease resistance, we could:
1. Change the material of the wire to one of lesser resistivity
2. Decrease the length of the wire
3. Increase the cross-sectional area of the wire
4. Decrease the temperature of the wire (very slight effect on resistance)
Relevant equations:
Current and resistance are inversely proportional to one another, assuming voltage is fixed. Since 
To decrease resistance, we could:
1. Change the material of the wire to one of lesser resistivity
2. Decrease the length of the wire
3. Increase the cross-sectional area of the wire
4. Decrease the temperature of the wire (very slight effect on resistance)
Compare your answer with the correct one above
A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.
If the current through the wire is measured to be 2A, how much thermal energy is being lost per second as soon as the wire is connected to the battery?
A battery is measured to have a potential of 5V. When connected to a wire with no resistors or other components, the voltage measured is 4.9V.
If the current through the wire is measured to be 2A, how much thermal energy is being lost per second as soon as the wire is connected to the battery?
First, we must know that the wire has some internal resistance  . To calculate this, we need to know the potential drop through the wire, which must be the difference we saw from the initial voltage reading to the second. This value, 0.1V, we plug into Ohm's law to calculate the resistance of the wire.
. To calculate this, we need to know the potential drop through the wire, which must be the difference we saw from the initial voltage reading to the second. This value, 0.1V, we plug into Ohm's law to calculate the resistance of the wire.



The question asks for energy lost per second; this value is equivalent to the power.

Use our values to solve.

First, we must know that the wire has some internal resistance 
The question asks for energy lost per second; this value is equivalent to the power.
Use our values to solve.
Compare your answer with the correct one above
A simple circuit contains two  resistors in parallel, connected to a 20V source. What power is being provided by the source to the circuit?
resistors in parallel, connected to a 20V source. What power is being provided by the source to the circuit?
A simple circuit contains two 
The power supplied to the circuit can be calculated using the equation:

To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:



Now that we have the resistance and the voltage, we can solve for the power.

The power supplied to the circuit can be calculated using the equation:
To use this equation, we need to find the equivalent resistance of the circuit. Use the equation for equivalent resistance in parallel:
Now that we have the resistance and the voltage, we can solve for the power.
Compare your answer with the correct one above
A lamp has a  bulb. If the house wiring provides
bulb. If the house wiring provides  to light up that bulb, how much current does the bulb draw?
to light up that bulb, how much current does the bulb draw?
A lamp has a 

The formula for power is , and we are given the following values.
and we are given the following values.


Solve for the current, 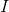 .
.

The formula for power is ,
Solve for the current, 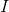
Compare your answer with the correct one above
A particle accelerator with a radius of 500 meters can have up to  protons circulating within it at once.
protons circulating within it at once.

How fast must the protons in the accelerator move in order to produce a current of 1A?
A particle accelerator with a radius of 500 meters can have up to 
How fast must the protons in the accelerator move in order to produce a current of 1A?
The current produced is the total charge that circulates the particle accelerator per unit time.
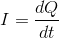
We calculate this by the equation:
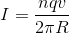
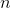 is the number of protons,
is the number of protons,  is the charge per proton,
is the charge per proton,  is the velocity of each proton, and
is the velocity of each proton, and  is the radius of the particle accelerator.
is the radius of the particle accelerator.
Using the given current, we then solve for the velocity:
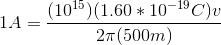

The current produced is the total charge that circulates the particle accelerator per unit time.
We calculate this by the equation:
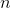



Using the given current, we then solve for the velocity:
Compare your answer with the correct one above
A lamp has a  bulb. If the house wiring provides
bulb. If the house wiring provides  to light up that bulb, how much current does the bulb draw?
to light up that bulb, how much current does the bulb draw?
A lamp has a 

The formula for power is , and we are given the following values.
and we are given the following values.


Solve for the current, 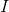 .
.

The formula for power is ,
Solve for the current, 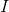
Compare your answer with the correct one above
A particle accelerator with a radius of 500 meters can have up to  protons circulating within it at once.
protons circulating within it at once.

How fast must the protons in the accelerator move in order to produce a current of 1A?
A particle accelerator with a radius of 500 meters can have up to 
How fast must the protons in the accelerator move in order to produce a current of 1A?
The current produced is the total charge that circulates the particle accelerator per unit time.
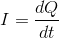
We calculate this by the equation:
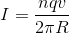
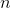 is the number of protons,
is the number of protons,  is the charge per proton,
is the charge per proton,  is the velocity of each proton, and
is the velocity of each proton, and  is the radius of the particle accelerator.
is the radius of the particle accelerator.
Using the given current, we then solve for the velocity:
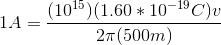

The current produced is the total charge that circulates the particle accelerator per unit time.
We calculate this by the equation:
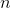



Using the given current, we then solve for the velocity:
Compare your answer with the correct one above
Three identical point charges with  are placed so that they form an equilateral triangle as shown in the figure. Find the electric potential at the center point (black dot) of that equilateral triangle, where this point is at a equal distance,
are placed so that they form an equilateral triangle as shown in the figure. Find the electric potential at the center point (black dot) of that equilateral triangle, where this point is at a equal distance,  , away from the three charges.
, away from the three charges.


Three identical point charges with 


The electric potential from point charges is  .
.
Knowing that all three charges are identical, and knowing that the center point at which we are calculating the electric potential is equal distance from the charges, we can multiply the electric potential equation by three.

Plug in the given values and solve for  .
.


The electric potential from point charges is 
Knowing that all three charges are identical, and knowing that the center point at which we are calculating the electric potential is equal distance from the charges, we can multiply the electric potential equation by three.
Plug in the given values and solve for 
Compare your answer with the correct one above
A proton moves in a straight line for a distance of  . Along this path, the electric field is uniform with a value of
. Along this path, the electric field is uniform with a value of  . Find the work done on the proton by the electric field.
. Find the work done on the proton by the electric field.
The charge of a proton is  .
.
A proton moves in a straight line for a distance of 

The charge of a proton is 
Work done by an electric field is given by the product of the charge of the particle, the electric field strength, and the distance travelled.

We are given the charge ( ), the distance (
), the distance ( ), and the field strength (
), and the field strength ( ), allowing us to calculate the work.
), allowing us to calculate the work.



Work done by an electric field is given by the product of the charge of the particle, the electric field strength, and the distance travelled.
We are given the charge (


Compare your answer with the correct one above
A proton moves in a straight line for a distance of  . Along this path, the electric field is uniform with a value of
. Along this path, the electric field is uniform with a value of  . Find the potential difference created by the movement.
. Find the potential difference created by the movement.
The charge of a proton is  .
.
A proton moves in a straight line for a distance of 

The charge of a proton is 
Potential difference is given by the change in voltage

Work done by an electric field is equal to the product of the electric force and the distance travelled. Electric force is equal to the product of the charge and the electric field strength.

The charges cancel, and we are able to solve for the potential difference.

Potential difference is given by the change in voltage
Work done by an electric field is equal to the product of the electric force and the distance travelled. Electric force is equal to the product of the charge and the electric field strength.
The charges cancel, and we are able to solve for the potential difference.
Compare your answer with the correct one above
The potential outside of a charged conducting cylinder with radius  and charge per unit length
and charge per unit length  is given by the below equation.
is given by the below equation.

What is the electric field at a point located at a distance  from the surface of the cylinder?
from the surface of the cylinder?
The potential outside of a charged conducting cylinder with radius 

What is the electric field at a point located at a distance 
The radial electric field outside the cylinder can be found using the equation  .
.
Using the formula given in the question, we can expand this equation.

Now, we can take the derivative and simplify.


The radial electric field outside the cylinder can be found using the equation 
Using the formula given in the question, we can expand this equation.
Now, we can take the derivative and simplify.
Compare your answer with the correct one above
For a ring of charge with radius  and total charge
and total charge  , the potential is given by
, the potential is given by  .
.
Find the expression for electric field produced by the ring.
For a ring of charge with radius 


Find the expression for electric field produced by the ring.
We know that  .
.
Using the given formula, we can find the electric potential expression for the ring.

Take the derivative and simplify.

We know that 
Using the given formula, we can find the electric potential expression for the ring.
Take the derivative and simplify.
Compare your answer with the correct one above
A negative charge of magnitude  is placed in a uniform electric field of
is placed in a uniform electric field of  , directed upwards. If the charge is moved
, directed upwards. If the charge is moved  upwards, how much work is done on the charge by the electric field in this process?
upwards, how much work is done on the charge by the electric field in this process?
A negative charge of magnitude 


Relevant equations:


Given:



First, find the potential difference between the initial and final positions:

2. Plug this potential difference into the work equation to solve for W:


Relevant equations:
Given:
First, find the potential difference between the initial and final positions:
2. Plug this potential difference into the work equation to solve for W:
Compare your answer with the correct one above
Three point charges are arranged around the origin, as shown.


Calculate the total electric potential at the origin due to the three point charges.

Three point charges are arranged around the origin, as shown.

Calculate the total electric potential at the origin due to the three point charges.
Electric potential is a scalar quantity given by the equation:

To find the total potential at the origin due to the three charges, add the potentials of each charge.




Electric potential is a scalar quantity given by the equation:
To find the total potential at the origin due to the three charges, add the potentials of each charge.
Compare your answer with the correct one above

A uniformly charged square frame of side length  carries a total charge
carries a total charge  . Calculate the potential at the center of the square.
. Calculate the potential at the center of the square.
You may wish to use the integral:


A uniformly charged square frame of side length 

You may wish to use the integral:
Calculate the potential due to one side of the bar, and then multiply this by  to get the total potential from all four sides. Orient the bar along the x-axis such that its endpoints are at
to get the total potential from all four sides. Orient the bar along the x-axis such that its endpoints are at  , and use the linear charge density
, and use the linear charge density  . The potential is therefore
. The potential is therefore


![=\frac{Q}{4\pi\epsilon_{0}a}\left[ \ln\left (\sqrt{x^2+\frac{a^2}{4}} +x\right )\right]_{-a/2}^{a/2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/891564/gif.latex)


Calculate the potential due to one side of the bar, and then multiply this by 


Compare your answer with the correct one above

Eight point charges of equal magnitude  are located at the vertices of a cube of side length
are located at the vertices of a cube of side length  . Calculate the potential at the center of the cube.
. Calculate the potential at the center of the cube.

Eight point charges of equal magnitude 

By the Pythagorean theorem, each charge is a distance

from the center of the cube, so the potential is


By the Pythagorean theorem, each charge is a distance
from the center of the cube, so the potential is
Compare your answer with the correct one above

A uniformly charged ring of radius  carries a total charge
carries a total charge  . Calculate the potential a distance
. Calculate the potential a distance  from the center, on the axis of the ring.
from the center, on the axis of the ring.

A uniformly charged ring of radius 


Use the linear charge density  and length element
and length element  . The distance from each point on the ring to the point on the axis is
. The distance from each point on the ring to the point on the axis is  . Lastly, integrate over
. Lastly, integrate over  from
from  to
to  to obtain
to obtain


Use the linear charge density 





Compare your answer with the correct one above