Understanding Vector and Scalar Quantities - AP Physics B
Card 0 of 4
Which answer choice below includes only scalar quantities?
Which answer choice below includes only scalar quantities?
Scalar quantities are those that can be described with magnitude only, as opposed to vectors, which include both magnitude and direction components. Distance, speed, and time are all scalars. Displacement is not a scalar, as it involves both the distance and the direction moved from a starting point. Velocity also includes a direction component, and is therefore a vector quantity.
Scalar quantities are those that can be described with magnitude only, as opposed to vectors, which include both magnitude and direction components. Distance, speed, and time are all scalars. Displacement is not a scalar, as it involves both the distance and the direction moved from a starting point. Velocity also includes a direction component, and is therefore a vector quantity.
Compare your answer with the correct one above
A ball is thrown at a velocity of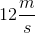 
at an angle of 
from the horizontal. What are the ball's horizontal and vertical velocities?
A ball is thrown at a velocity of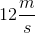
The velocity of 
can be broken into horizontal and vertical components by using trigonometry. Think of the figure below, where x and y velocity components of the total velocity are shown.
Use the total velocity, the x-component, and the y-component to form a right triangle below.
Treating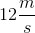 
as the hypotenuse, x-component as the leg adjacent, and y-component as the leg opposite, you can conclude that the velocities are related through trigonometric identities.
Plugging in the given values, we can solve for the x and y velocity components.
The velocity of
Use the total velocity, the x-component, and the y-component to form a right triangle below.
Treating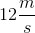
Plugging in the given values, we can solve for the x and y velocity components.
Compare your answer with the correct one above
Which answer choice below includes only scalar quantities?
Which answer choice below includes only scalar quantities?
Scalar quantities are those that can be described with magnitude only, as opposed to vectors, which include both magnitude and direction components. Distance, speed, and time are all scalars. Displacement is not a scalar, as it involves both the distance and the direction moved from a starting point. Velocity also includes a direction component, and is therefore a vector quantity.
Scalar quantities are those that can be described with magnitude only, as opposed to vectors, which include both magnitude and direction components. Distance, speed, and time are all scalars. Displacement is not a scalar, as it involves both the distance and the direction moved from a starting point. Velocity also includes a direction component, and is therefore a vector quantity.
Compare your answer with the correct one above
A ball is thrown at a velocity of 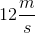at an angle of from the horizontal. What are the ball's horizontal and vertical velocities?
A ball is thrown at a velocity of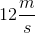
The velocity of can be broken into horizontal and vertical components by using trigonometry. Think of the figure below, where x and y velocity components of the total velocity are shown.
Use the total velocity, the x-component, and the y-component to form a right triangle below.
Treating 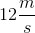as the hypotenuse, x-component as the leg adjacent, and y-component as the leg opposite, you can conclude that the velocities are related through trigonometric identities.
Plugging in the given values, we can solve for the x and y velocity components.
The velocity of
Use the total velocity, the x-component, and the y-component to form a right triangle below.
Treating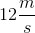
Plugging in the given values, we can solve for the x and y velocity components.
Compare your answer with the correct one above