Understanding Linear-Rotational Equivalents - AP Physics B
Card 0 of 2
A wheel of radius 
rolls along a flat floor and makes 
rotations over a period of time. What distance 
has the wheel traveled?
A wheel of radius
In order to find the distance the wheel travels, we need a way to convert angular displacement to linear displacement. We know that the circumference of a circle (or a wheel, in this case) is 
. This means that in one rotation, the wheel would travel a distance equal to its circumference.
Distance of one rotation equals: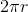 
.
Since the wheel travels 
rotations, the total distance that the wheel travels will be equal to the distance traveled by one rotation multiplied by the number of rotations.
Distance of 
rotations equals: 
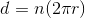
In order to find the distance the wheel travels, we need a way to convert angular displacement to linear displacement. We know that the circumference of a circle (or a wheel, in this case) is
Distance of one rotation equals: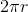
Since the wheel travels
Distance of
Compare your answer with the correct one above
A wheel of radius rolls along a flat floor and makes rotations over a period of time. What distance has the wheel traveled?
A wheel of radius
In order to find the distance the wheel travels, we need a way to convert angular displacement to linear displacement. We know that the circumference of a circle (or a wheel, in this case) is . This means that in one rotation, the wheel would travel a distance equal to its circumference.
Distance of one rotation equals: .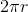
Since the wheel travels rotations, the total distance that the wheel travels will be equal to the distance traveled by one rotation multiplied by the number of rotations.
Distance of rotations equals:
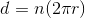
In order to find the distance the wheel travels, we need a way to convert angular displacement to linear displacement. We know that the circumference of a circle (or a wheel, in this case) is
Distance of one rotation equals: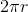
Since the wheel travels
Distance of
Compare your answer with the correct one above