Electricity and Magnetism - AP Physics B
Card 0 of 20
Consider two resistors connected in series. Which of the following is true regarding its voltage, current, and power?
Consider two resistors connected in series. Which of the following is true regarding its voltage, current, and power?
Since the resistors are connected in series, they will have the same current flowing through them. In series current is constant across resistors, and in parallel voltage is constant across resistors.
Remember the equations for voltage and power. The equation for voltage is Ohm's law:

Power can be written in terms of voltage and resistance, but in this problem only the current is held constant (because the resistors are in series) while the voltage of the resistors is different. The appropriate equation to use for comparison is:

From the equations you can deduce that increasing resistance will increase both voltage and power. The best answer is that current through both resistors is the same, but the larger resistor will have higher voltage and power dissipation.
Since the resistors are connected in series, they will have the same current flowing through them. In series current is constant across resistors, and in parallel voltage is constant across resistors.
Remember the equations for voltage and power. The equation for voltage is Ohm's law:
Power can be written in terms of voltage and resistance, but in this problem only the current is held constant (because the resistors are in series) while the voltage of the resistors is different. The appropriate equation to use for comparison is:
From the equations you can deduce that increasing resistance will increase both voltage and power. The best answer is that current through both resistors is the same, but the larger resistor will have higher voltage and power dissipation.
Compare your answer with the correct one above
Which of the following is not equivalent to a unit of power?
Which of the following is not equivalent to a unit of power?
The standard unit for power is Watts, but other equivalent units can be derived from the equations for power.
Remember that power is defined as work per unit time:

The units from this equation will be Joules per second, eliminating that answer choice.
In terms of circuits, power is defined as the product of current and voltage, giving the units Ampere-Volts:

If you combine Ohm’s law and the definition of power you can rewrite the equation for power as follows:

These units will be Amperes squared times Ohms.
The only answer choice you are left with is Ohm-Volts. Power in terms of resistance and voltage is:

The standard unit for power is Watts, but other equivalent units can be derived from the equations for power.
Remember that power is defined as work per unit time:
The units from this equation will be Joules per second, eliminating that answer choice.
In terms of circuits, power is defined as the product of current and voltage, giving the units Ampere-Volts:
If you combine Ohm’s law and the definition of power you can rewrite the equation for power as follows:
These units will be Amperes squared times Ohms.
The only answer choice you are left with is Ohm-Volts. Power in terms of resistance and voltage is:
Compare your answer with the correct one above
Consider two resistors connected in series. Which of the following is true regarding its voltage, current, and power?
Consider two resistors connected in series. Which of the following is true regarding its voltage, current, and power?
Since the resistors are connected in series, they will have the same current flowing through them. In series current is constant across resistors, and in parallel voltage is constant across resistors.
Remember the equations for voltage and power. The equation for voltage is Ohm's law:

Power can be written in terms of voltage and resistance, but in this problem only the current is held constant (because the resistors are in series) while the voltage of the resistors is different. The appropriate equation to use for comparison is:

From the equations you can deduce that increasing resistance will increase both voltage and power. The best answer is that current through both resistors is the same, but the larger resistor will have higher voltage and power dissipation.
Since the resistors are connected in series, they will have the same current flowing through them. In series current is constant across resistors, and in parallel voltage is constant across resistors.
Remember the equations for voltage and power. The equation for voltage is Ohm's law:
Power can be written in terms of voltage and resistance, but in this problem only the current is held constant (because the resistors are in series) while the voltage of the resistors is different. The appropriate equation to use for comparison is:
From the equations you can deduce that increasing resistance will increase both voltage and power. The best answer is that current through both resistors is the same, but the larger resistor will have higher voltage and power dissipation.
Compare your answer with the correct one above
Which of the following is not equivalent to a unit of power?
Which of the following is not equivalent to a unit of power?
The standard unit for power is Watts, but other equivalent units can be derived from the equations for power.
Remember that power is defined as work per unit time:

The units from this equation will be Joules per second, eliminating that answer choice.
In terms of circuits, power is defined as the product of current and voltage, giving the units Ampere-Volts:

If you combine Ohm’s law and the definition of power you can rewrite the equation for power as follows:

These units will be Amperes squared times Ohms.
The only answer choice you are left with is Ohm-Volts. Power in terms of resistance and voltage is:

The standard unit for power is Watts, but other equivalent units can be derived from the equations for power.
Remember that power is defined as work per unit time:
The units from this equation will be Joules per second, eliminating that answer choice.
In terms of circuits, power is defined as the product of current and voltage, giving the units Ampere-Volts:
If you combine Ohm’s law and the definition of power you can rewrite the equation for power as follows:
These units will be Amperes squared times Ohms.
The only answer choice you are left with is Ohm-Volts. Power in terms of resistance and voltage is:
Compare your answer with the correct one above
A proton traveling at 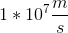 in a horizontal plane passes through an opening into a mass spectrometer with a uniform
in a horizontal plane passes through an opening into a mass spectrometer with a uniform  magnetic field directed upward. The particle then moves in a circular path through
magnetic field directed upward. The particle then moves in a circular path through  and crashes into the wall of the spectrometer adjacent to the entrance opening. How far down from the entrance is the proton when it crashes into the wall?
and crashes into the wall of the spectrometer adjacent to the entrance opening. How far down from the entrance is the proton when it crashes into the wall?
The proton’s mass is  and its electric charge is
and its electric charge is  .
.
A proton traveling at 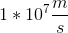


The proton’s mass is 


A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:

 is the charge,
is the charge,  is the particle speed, and
is the particle speed, and  is the magnetic field strength. This force is always directed perpendicular to the particle’s direction of travel at that moment, and thus acts as a centripetal force. This force is also given by the equation:
is the magnetic field strength. This force is always directed perpendicular to the particle’s direction of travel at that moment, and thus acts as a centripetal force. This force is also given by the equation:

We can set these two equations equal to one another, allowing us to solve for the radius of the arc.

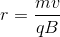
Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).

Twice this value is the lateral offset of its crash point from the entrance:


A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:



We can set these two equations equal to one another, allowing us to solve for the radius of the arc.
Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).
Twice this value is the lateral offset of its crash point from the entrance:
Compare your answer with the correct one above
A proton traveling at 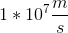 in a horizontal plane passes through an opening into a mass spectrometer with a uniform
in a horizontal plane passes through an opening into a mass spectrometer with a uniform  magnetic field directed upward. The particle then moves in a circular path through
magnetic field directed upward. The particle then moves in a circular path through  and crashes into the wall of the spectrometer adjacent to the entrance opening. How far down from the entrance is the proton when it crashes into the wall?
and crashes into the wall of the spectrometer adjacent to the entrance opening. How far down from the entrance is the proton when it crashes into the wall?
The proton’s mass is  and its electric charge is
and its electric charge is  .
.
A proton traveling at 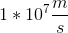


The proton’s mass is 


A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:

 is the charge,
is the charge,  is the particle speed, and
is the particle speed, and  is the magnetic field strength. This force is always directed perpendicular to the particle’s direction of travel at that moment, and thus acts as a centripetal force. This force is also given by the equation:
is the magnetic field strength. This force is always directed perpendicular to the particle’s direction of travel at that moment, and thus acts as a centripetal force. This force is also given by the equation:

We can set these two equations equal to one another, allowing us to solve for the radius of the arc.

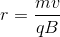
Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).

Twice this value is the lateral offset of its crash point from the entrance:


A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:



We can set these two equations equal to one another, allowing us to solve for the radius of the arc.
Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).
Twice this value is the lateral offset of its crash point from the entrance:
Compare your answer with the correct one above
A capacitor has a stored charge of  and a potential energy of
and a potential energy of  . What is the voltage across the capacitor?
. What is the voltage across the capacitor?
A capacitor has a stored charge of 

To solve this problem, you need to use the following two equations:


By substituting into the second equation you can write the change in potential energy in terms of voltage and charge.

Rearranging the previous equation will allow us to solve for the voltage.

Use the given values for stored potential energy and charge to solve for the voltage.


To solve this problem, you need to use the following two equations:
By substituting into the second equation you can write the change in potential energy in terms of voltage and charge.
Rearranging the previous equation will allow us to solve for the voltage.
Use the given values for stored potential energy and charge to solve for the voltage.
Compare your answer with the correct one above
Which of the following is equal to the time constant of an RC circuit?
Which of the following is equal to the time constant of an RC circuit?
The definition of a time constant for an RC circuit is the product of resistance and charge:

This is defined as the time it takes the capacitor to reach a charge that is around 63% of the maximum charge. It is also the time it takes to discharge around 37% of the charge. This value is commonly used to determine the amount of charge a capacitor has or the amount of current flowing through the capacitor at any given time point.
The definition of a time constant for an RC circuit is the product of resistance and charge:
This is defined as the time it takes the capacitor to reach a charge that is around 63% of the maximum charge. It is also the time it takes to discharge around 37% of the charge. This value is commonly used to determine the amount of charge a capacitor has or the amount of current flowing through the capacitor at any given time point.
Compare your answer with the correct one above
Which of the following statements is false regarding capacitors?
I. A larger capacitor stores more energy
II. Capacitors connected in parallel have the same voltage drop
III. Increasing the distance between the two plates increases the capacitance
Which of the following statements is false regarding capacitors?
I. A larger capacitor stores more energy
II. Capacitors connected in parallel have the same voltage drop
III. Increasing the distance between the two plates increases the capacitance
Recall the equation for potential energy in terms of capacitance:

According to the equation above, an increase in capacitance will lead to decrease in the amount of energy stored. This means that a larger capacitor will store less energy; therefore, statement I is false.
Any circuit elements connected in parallel will always have the same voltage drop. This applies to resistors, capacitors, and inductors. Statement II is true.
Remember that capacitance is defined as follows:

In this equation,  is the area of the plates and
is the area of the plates and  is distance between the plates. Increasing
is distance between the plates. Increasing  will lead to a decrease in capacitance; therefore, statement III is false.
will lead to a decrease in capacitance; therefore, statement III is false.
Recall the equation for potential energy in terms of capacitance:
According to the equation above, an increase in capacitance will lead to decrease in the amount of energy stored. This means that a larger capacitor will store less energy; therefore, statement I is false.
Any circuit elements connected in parallel will always have the same voltage drop. This applies to resistors, capacitors, and inductors. Statement II is true.
Remember that capacitance is defined as follows:
In this equation, 


Compare your answer with the correct one above
A capacitor has a stored charge of  and a potential energy of
and a potential energy of  . What is the voltage across the capacitor?
. What is the voltage across the capacitor?
A capacitor has a stored charge of 

To solve this problem, you need to use the following two equations:


By substituting into the second equation you can write the change in potential energy in terms of voltage and charge.

Rearranging the previous equation will allow us to solve for the voltage.

Use the given values for stored potential energy and charge to solve for the voltage.


To solve this problem, you need to use the following two equations:
By substituting into the second equation you can write the change in potential energy in terms of voltage and charge.
Rearranging the previous equation will allow us to solve for the voltage.
Use the given values for stored potential energy and charge to solve for the voltage.
Compare your answer with the correct one above
Which of the following is equal to the time constant of an RC circuit?
Which of the following is equal to the time constant of an RC circuit?
The definition of a time constant for an RC circuit is the product of resistance and charge:

This is defined as the time it takes the capacitor to reach a charge that is around 63% of the maximum charge. It is also the time it takes to discharge around 37% of the charge. This value is commonly used to determine the amount of charge a capacitor has or the amount of current flowing through the capacitor at any given time point.
The definition of a time constant for an RC circuit is the product of resistance and charge:
This is defined as the time it takes the capacitor to reach a charge that is around 63% of the maximum charge. It is also the time it takes to discharge around 37% of the charge. This value is commonly used to determine the amount of charge a capacitor has or the amount of current flowing through the capacitor at any given time point.
Compare your answer with the correct one above
Which of the following statements is false regarding capacitors?
I. A larger capacitor stores more energy
II. Capacitors connected in parallel have the same voltage drop
III. Increasing the distance between the two plates increases the capacitance
Which of the following statements is false regarding capacitors?
I. A larger capacitor stores more energy
II. Capacitors connected in parallel have the same voltage drop
III. Increasing the distance between the two plates increases the capacitance
Recall the equation for potential energy in terms of capacitance:

According to the equation above, an increase in capacitance will lead to decrease in the amount of energy stored. This means that a larger capacitor will store less energy; therefore, statement I is false.
Any circuit elements connected in parallel will always have the same voltage drop. This applies to resistors, capacitors, and inductors. Statement II is true.
Remember that capacitance is defined as follows:

In this equation,  is the area of the plates and
is the area of the plates and  is distance between the plates. Increasing
is distance between the plates. Increasing  will lead to a decrease in capacitance; therefore, statement III is false.
will lead to a decrease in capacitance; therefore, statement III is false.
Recall the equation for potential energy in terms of capacitance:
According to the equation above, an increase in capacitance will lead to decrease in the amount of energy stored. This means that a larger capacitor will store less energy; therefore, statement I is false.
Any circuit elements connected in parallel will always have the same voltage drop. This applies to resistors, capacitors, and inductors. Statement II is true.
Remember that capacitance is defined as follows:
In this equation, 


Compare your answer with the correct one above
A charge travels along a copper wire that has a resistance of  . It takes two seconds for the charge to travel along the wire. The potential difference in the wire is
. It takes two seconds for the charge to travel along the wire. The potential difference in the wire is 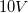 . What is the charge of the particle?
. What is the charge of the particle?
A charge travels along a copper wire that has a resistance of 
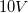
To solve this question you need to use the Ohm’s law and the definition of an electric current. Ohm’s law states that voltage is the product of current and resistance:

The definition of electric current is given by the charge per unit time:

Using these equations it is possible to solve for the charge. The trick is to first solve for the current using Ohm’s law and the given voltage and resistance.


Now that we know the current and the time, we can solve for the charge using our second equation.

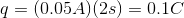
To solve this question you need to use the Ohm’s law and the definition of an electric current. Ohm’s law states that voltage is the product of current and resistance:
The definition of electric current is given by the charge per unit time:
Using these equations it is possible to solve for the charge. The trick is to first solve for the current using Ohm’s law and the given voltage and resistance.
Now that we know the current and the time, we can solve for the charge using our second equation.
Compare your answer with the correct one above
A charge travels along a copper wire that has a resistance of  . It takes two seconds for the charge to travel along the wire. The potential difference in the wire is
. It takes two seconds for the charge to travel along the wire. The potential difference in the wire is 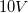 . What is the charge of the particle?
. What is the charge of the particle?
A charge travels along a copper wire that has a resistance of 
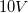
To solve this question you need to use the Ohm’s law and the definition of an electric current. Ohm’s law states that voltage is the product of current and resistance:

The definition of electric current is given by the charge per unit time:

Using these equations it is possible to solve for the charge. The trick is to first solve for the current using Ohm’s law and the given voltage and resistance.


Now that we know the current and the time, we can solve for the charge using our second equation.

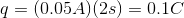
To solve this question you need to use the Ohm’s law and the definition of an electric current. Ohm’s law states that voltage is the product of current and resistance:
The definition of electric current is given by the charge per unit time:
Using these equations it is possible to solve for the charge. The trick is to first solve for the current using Ohm’s law and the given voltage and resistance.
Now that we know the current and the time, we can solve for the charge using our second equation.
Compare your answer with the correct one above
Charges A and B are placed a distance of  from one another. The charge of particle A is
from one another. The charge of particle A is  whereas the charge of particle B is
whereas the charge of particle B is  . Charge B experiences an electrostatic force of
. Charge B experiences an electrostatic force of  from charge A. Similarly, charge A experiences an electrostatic force of
from charge A. Similarly, charge A experiences an electrostatic force of  from charge B.
from charge B.
A student places these two charges in a vacuum medium and measures  . A second student places these two charges in a glass medium and measures
. A second student places these two charges in a glass medium and measures  . What is ratio of the force measured in the glass medium to the force measured in the vacuum?
. What is ratio of the force measured in the glass medium to the force measured in the vacuum?
The dielectric constant of glass is  .
.
Charges A and B are placed a distance of 




A student places these two charges in a vacuum medium and measures 

The dielectric constant of glass is 
You can simplify this question tremendously by using the definition of a dielectric constant. Dielectric constant is defined as the ratio of the electrostatic force in vacuum to the electrostatic force in the medium (in this case glass).

The question is asking for the reciprocal of this value: the ratio of the force in glass to the force in the vacuum. Our answer is calculated by taking the reciprocal of the dielectric constant of glass.

You can simplify this question tremendously by using the definition of a dielectric constant. Dielectric constant is defined as the ratio of the electrostatic force in vacuum to the electrostatic force in the medium (in this case glass).
The question is asking for the reciprocal of this value: the ratio of the force in glass to the force in the vacuum. Our answer is calculated by taking the reciprocal of the dielectric constant of glass.
Compare your answer with the correct one above
How much work is done by the electric field moving an electron along an equipotential surface with a potential of  ?
?

How much work is done by the electric field moving an electron along an equipotential surface with a potential of 
Moving a charge along an equipotential surface will involve no work done by the electric field. The potential is constant throughout an equipotential surface; therefore, the potential difference experienced by the electron will be zero. Remember that energy is dependent on the potential difference.

If the potential difference is zero then the energy (and work) will be zero.
Moving a charge along an equipotential surface will involve no work done by the electric field. The potential is constant throughout an equipotential surface; therefore, the potential difference experienced by the electron will be zero. Remember that energy is dependent on the potential difference.
If the potential difference is zero then the energy (and work) will be zero.
Compare your answer with the correct one above
Charges A and B are placed a distance of  from one another. The charge of particle A is
from one another. The charge of particle A is  whereas the charge of particle B is
whereas the charge of particle B is  . Charge B experiences an electrostatic force of
. Charge B experiences an electrostatic force of  from charge A. Similarly, charge A experiences an electrostatic force of
from charge A. Similarly, charge A experiences an electrostatic force of  from charge B.
from charge B.
A student places these two charges in a vacuum medium and measures  . A second student places these two charges in a glass medium and measures
. A second student places these two charges in a glass medium and measures  . What is ratio of the force measured in the glass medium to the force measured in the vacuum?
. What is ratio of the force measured in the glass medium to the force measured in the vacuum?
The dielectric constant of glass is  .
.
Charges A and B are placed a distance of 




A student places these two charges in a vacuum medium and measures 

The dielectric constant of glass is 
You can simplify this question tremendously by using the definition of a dielectric constant. Dielectric constant is defined as the ratio of the electrostatic force in vacuum to the electrostatic force in the medium (in this case glass).

The question is asking for the reciprocal of this value: the ratio of the force in glass to the force in the vacuum. Our answer is calculated by taking the reciprocal of the dielectric constant of glass.

You can simplify this question tremendously by using the definition of a dielectric constant. Dielectric constant is defined as the ratio of the electrostatic force in vacuum to the electrostatic force in the medium (in this case glass).
The question is asking for the reciprocal of this value: the ratio of the force in glass to the force in the vacuum. Our answer is calculated by taking the reciprocal of the dielectric constant of glass.
Compare your answer with the correct one above
How much work is done by the electric field moving an electron along an equipotential surface with a potential of  ?
?

How much work is done by the electric field moving an electron along an equipotential surface with a potential of 
Moving a charge along an equipotential surface will involve no work done by the electric field. The potential is constant throughout an equipotential surface; therefore, the potential difference experienced by the electron will be zero. Remember that energy is dependent on the potential difference.

If the potential difference is zero then the energy (and work) will be zero.
Moving a charge along an equipotential surface will involve no work done by the electric field. The potential is constant throughout an equipotential surface; therefore, the potential difference experienced by the electron will be zero. Remember that energy is dependent on the potential difference.
If the potential difference is zero then the energy (and work) will be zero.
Compare your answer with the correct one above
Which of the following changes to a copper wire will lead to the greatest decrease in voltage?
Which of the following changes to a copper wire will lead to the greatest decrease in voltage?
According to Ohm’s law a decrease in current and/or resistance will lead to a decrease in voltage, since voltage is directly proportional to both current and resistance.

Increasing the current will not decrease voltage. Remember that resistance is defined as:

In this formula,  is the resistivity,
is the resistivity,  is the length of the wire, and
is the length of the wire, and  is the cross-sectional area of the wire. Increasing length will lead to an increase in resistance and voltage; however, increasing the area will lead to a decrease in resistance and, subsequently, a decrease in voltage.
is the cross-sectional area of the wire. Increasing length will lead to an increase in resistance and voltage; however, increasing the area will lead to a decrease in resistance and, subsequently, a decrease in voltage.
The only answer that will lead to a decrease in voltage is the choice to increase the cross-sectional area of the wire.
Replacing the copper wire with a more conductive material will increase the resistivity, which will subsequently increase resistance and voltage.
According to Ohm’s law a decrease in current and/or resistance will lead to a decrease in voltage, since voltage is directly proportional to both current and resistance.
Increasing the current will not decrease voltage. Remember that resistance is defined as:
In this formula, 


The only answer that will lead to a decrease in voltage is the choice to increase the cross-sectional area of the wire.
Replacing the copper wire with a more conductive material will increase the resistivity, which will subsequently increase resistance and voltage.
Compare your answer with the correct one above
A student assembles a circuit made up of a voltage source and two resistors. All three circuit elements are connected in parallel. The voltage across the voltage source is  and the resistance of the resistors are
and the resistance of the resistors are  and
and  respectively. Which of the following is true of this circuit?
respectively. Which of the following is true of this circuit?
A student assembles a circuit made up of a voltage source and two resistors. All three circuit elements are connected in parallel. The voltage across the voltage source is 


When circuit elements, such as resistors, are connected in parallel they will have the same voltage drop. The current through the  resistor will be greater than current through the
resistor will be greater than current through the  resistor, but their voltages will be equal. According to Ohm’s law the current flowing through the smaller resistor will be larger. Ohm’s law can be rearranged to solve for current as follows:
resistor, but their voltages will be equal. According to Ohm’s law the current flowing through the smaller resistor will be larger. Ohm’s law can be rearranged to solve for current as follows:

Since voltage is the same across resistors, the lower resistance ( ) will have more current flowing through it since current is inversely proportional to resistance.
) will have more current flowing through it since current is inversely proportional to resistance.
When circuit elements, such as resistors, are connected in parallel they will have the same voltage drop. The current through the 

Since voltage is the same across resistors, the lower resistance (
Compare your answer with the correct one above