Magnetism and Electromagnetism - AP Physics 2
Card 0 of 20
There is a particle with a charge of  moving
moving  perpendicular through a magnetic field with a strength of
perpendicular through a magnetic field with a strength of  . What is the force on the particle?
. What is the force on the particle?
There is a particle with a charge of 


The equation for force on a moving charged particle in a magnetic field is
 .
.
Because the charge is moving perpendicularly through the magnetic field, we don't have to worry about the cross product, and the equation becomes simple multiplication.



Therefore, the force experienced by the particle is 3619N.
The equation for force on a moving charged particle in a magnetic field is

Because the charge is moving perpendicularly through the magnetic field, we don't have to worry about the cross product, and the equation becomes simple multiplication.
Therefore, the force experienced by the particle is 3619N.
Compare your answer with the correct one above

A conductive rod is moving through a region of magnetic field, directed out of the page as diagrammed above. As a result of its motion, the mobile charge in the rod separates, creating an electric potential across the length of the rod. The length of the rod is 0.12m and the magnitude of the magnetic field is 0.022T. If the rod is moving with velocity  , what is the magnitude and direction of the potential from one end of the rod to the other?
, what is the magnitude and direction of the potential from one end of the rod to the other?

A conductive rod is moving through a region of magnetic field, directed out of the page as diagrammed above. As a result of its motion, the mobile charge in the rod separates, creating an electric potential across the length of the rod. The length of the rod is 0.12m and the magnitude of the magnetic field is 0.022T. If the rod is moving with velocity 
For a conductor moving in a magnetic field, cutting straight across the field lines, a potential is generated  where
where  is the potential or EMF,
is the potential or EMF,  is the magnetic field strength, and
is the magnetic field strength, and  is the conductor's velocity relative to the field.
is the conductor's velocity relative to the field.

As the rod moves, the positive charge feels an upward-directed force by the right-hand rule, and the negative a downward force resulting in the top being at a higher potential than the bottom of the rod.
For a conductor moving in a magnetic field, cutting straight across the field lines, a potential is generated 



As the rod moves, the positive charge feels an upward-directed force by the right-hand rule, and the negative a downward force resulting in the top being at a higher potential than the bottom of the rod.
Compare your answer with the correct one above

A conductive rod is moving through a region of magnetic field, as diagrammed above. As a result of its motion, mobile charge carriers in the conductor separate, creating an electric potential across the rod. When, if ever, do the charge carriers cease this motion?

A conductive rod is moving through a region of magnetic field, as diagrammed above. As a result of its motion, mobile charge carriers in the conductor separate, creating an electric potential across the rod. When, if ever, do the charge carriers cease this motion?
The separated charge creates a potential  . This potential results in an electric field
. This potential results in an electric field  When this induced electric field creates a force
When this induced electric field creates a force  equal to the magnetic force
equal to the magnetic force  on the mobile charge carriers, motion stops. Of course, if an electric circuit is created drawing current from the rod, motion will resume to rebuild the field.
on the mobile charge carriers, motion stops. Of course, if an electric circuit is created drawing current from the rod, motion will resume to rebuild the field.
The separated charge creates a potential 



Compare your answer with the correct one above
A magnetic rod is inside a coil of wire which is connected to an ammeter. If the rod is stationary, which of the following statements are true?
A magnetic rod is inside a coil of wire which is connected to an ammeter. If the rod is stationary, which of the following statements are true?
Current is induced in wire when the magnetic flux changes. When the magnetic rod is in motion, the flux is changing, so current is induced. If the coil were expanded or contracted with the rod still there, the flux would change and current would be induced. In our case, the rod is stationary and the coil isn't changing shape. Therefore, the flux is not changing, so there is no current being induced. Additionally, there's no reason for the rod to lose its magnetic property.
Current is induced in wire when the magnetic flux changes. When the magnetic rod is in motion, the flux is changing, so current is induced. If the coil were expanded or contracted with the rod still there, the flux would change and current would be induced. In our case, the rod is stationary and the coil isn't changing shape. Therefore, the flux is not changing, so there is no current being induced. Additionally, there's no reason for the rod to lose its magnetic property.
Compare your answer with the correct one above
Suppose the induced electromotive force of a double loop wire has a magnitude of  when the change in magnetic flux is
when the change in magnetic flux is  . How much time has elapsed for the flux change?
. How much time has elapsed for the flux change?
Suppose the induced electromotive force of a double loop wire has a magnitude of 

Write the formula for induced electromotive force.

Since there are two loops,  .
.


Solve for  .
.

Write the formula for induced electromotive force.
Since there are two loops, 
Solve for 
Compare your answer with the correct one above

A system consists of two rails, whose resistance is zero, a conductive bar, whose resistance is also zero, and a resistor whose resistance, 0.02 Ohms. The bar remains in contact with the rails as it slides to the right with a velocity  . The distance from one rail to the other is 0.07m. The magnetic field, which is directed out of the page, has a magnitude of 0.0015T. What is the magnitude and direction of current in the resistor?
. The distance from one rail to the other is 0.07m. The magnetic field, which is directed out of the page, has a magnitude of 0.0015T. What is the magnitude and direction of current in the resistor?

A system consists of two rails, whose resistance is zero, a conductive bar, whose resistance is also zero, and a resistor whose resistance, 0.02 Ohms. The bar remains in contact with the rails as it slides to the right with a velocity 
When a conductor moves through a magnetic field in such a way that it cuts through magnetic field lines, the mobile charge carriers separate due to the magnetic force on them, creating a potential  . Since there is no resistance anywhere else in the circuit, all of this potential is lost in the resistor, so we can apply Ohm's law:
. Since there is no resistance anywhere else in the circuit, all of this potential is lost in the resistor, so we can apply Ohm's law:



Because the positive charge in the rod feels an upward force due to the right-hand rule, the top of the rod has a greater potential than the bottom, and current flows counterclockwise around the circuit, resulting in a downward direction in the resistor.
When a conductor moves through a magnetic field in such a way that it cuts through magnetic field lines, the mobile charge carriers separate due to the magnetic force on them, creating a potential 
Because the positive charge in the rod feels an upward force due to the right-hand rule, the top of the rod has a greater potential than the bottom, and current flows counterclockwise around the circuit, resulting in a downward direction in the resistor.
Compare your answer with the correct one above

A  resistor is connected to a coil with
resistor is connected to a coil with  turns and a cross sectional area of
turns and a cross sectional area of  . A magnet is lowered as shown in the figure. The magnetic field increases from
. A magnet is lowered as shown in the figure. The magnetic field increases from  to
to  in
in  . Find the magnitude of the current going through the resistor.
. Find the magnitude of the current going through the resistor.

A 





There is a change in flux produced by the changing magnetic field which is given by

where  is the cross sectional area of the coil,
is the cross sectional area of the coil,  is the change in magnetic field, and
is the change in magnetic field, and  is the angle of the field lines relative to the normal of the cross section of the coil.
is the angle of the field lines relative to the normal of the cross section of the coil.
In this case the magnet is perpendicular to the cross section of the coil and so


The change in magnetic field is just the final given value minus the intial value. Faraday's Law says that an emf will be generated by a change in flux,

where  is the number of turns in the coil. Plugging in the change in flux gives
is the number of turns in the coil. Plugging in the change in flux gives

The change in time is just  since we can start our clock at zero. The current can be found using Ohm's Law where
since we can start our clock at zero. The current can be found using Ohm's Law where

There is a change in flux produced by the changing magnetic field which is given by
where 


In this case the magnet is perpendicular to the cross section of the coil and so
The change in magnetic field is just the final given value minus the intial value. Faraday's Law says that an emf will be generated by a change in flux,
where 
The change in time is just 
Compare your answer with the correct one above
Suppose that a proton moves perpendicularly through a magnetic field at a speed of  . If this proton experiences a magnetic force of
. If this proton experiences a magnetic force of  , what is the strength of the magnetic field?
, what is the strength of the magnetic field?
 .
.
Suppose that a proton moves perpendicularly through a magnetic field at a speed of 


To solve this question, we need to relate the speed and charge of the particle with the magnetic force it experiences in order to solve for the magnetic field strength. Thus, we'll need to use the following equation:

Also, we are told that the particle is moving perpendicularly to the magnetic field.



Rearrange to solve for the magnetic field, then plug in known values and solve.



To solve this question, we need to relate the speed and charge of the particle with the magnetic force it experiences in order to solve for the magnetic field strength. Thus, we'll need to use the following equation:
Also, we are told that the particle is moving perpendicularly to the magnetic field.
Rearrange to solve for the magnetic field, then plug in known values and solve.
Compare your answer with the correct one above
Suppose that a positively charged particle with charge  moves in a circular path of radius
moves in a circular path of radius  in a constant magnetic field of strength
in a constant magnetic field of strength  . If the magnetic field strength is doubled to
. If the magnetic field strength is doubled to  , what effect does this have on the radius of the circular path that this charge takes?
, what effect does this have on the radius of the circular path that this charge takes?
Suppose that a positively charged particle with charge 



To answer this question, we need to realize that the particle is moving in a circular path because of some sort of centripetal force. Since the charge is moving while within a constant magnetic field, we can conclude that it is the magnetic force that is responsible for the centripetal force that keeps this charge moving in a circle. Thus, we need to relate the centripetal force to the magnetic force.




The above equation shows us that the radius of the circular path is directy proportional to the mass and velocity of the particle, and inversely proportional to the charge of the particle and the magnetic field strength. Thus, if the value of the magnetic field is doubled, the above equation predicts that the value of the radius would be cut in half.
To answer this question, we need to realize that the particle is moving in a circular path because of some sort of centripetal force. Since the charge is moving while within a constant magnetic field, we can conclude that it is the magnetic force that is responsible for the centripetal force that keeps this charge moving in a circle. Thus, we need to relate the centripetal force to the magnetic force.
The above equation shows us that the radius of the circular path is directy proportional to the mass and velocity of the particle, and inversely proportional to the charge of the particle and the magnetic field strength. Thus, if the value of the magnetic field is doubled, the above equation predicts that the value of the radius would be cut in half.
Compare your answer with the correct one above
 loops of current carrying wire form a solenoid of length
loops of current carrying wire form a solenoid of length  that carries
that carries  and have radius
and have radius  . Determine the magnetic field at the center of the solenoid.
. Determine the magnetic field at the center of the solenoid.




Using:

Where:
 is the magnetic field
is the magnetic field
 is the number of coils
is the number of coils
 is the current in the solenoid
is the current in the solenoid
 is the length of the solenoid
is the length of the solenoid
 is
is 
Plugging in values:


Using:
Where:





Plugging in values:
Compare your answer with the correct one above
There is a loop with a radius of  and a current of
and a current of  . Determine the magnitude of the magnetic field at the center of the loop.
. Determine the magnitude of the magnetic field at the center of the loop.
There is a loop with a radius of 

Using the Biot-Savart law:

Where  is the radius of the loop
is the radius of the loop
 is the current
is the current
 is the distance from the center of the loop
is the distance from the center of the loop

Plugging in values:


Using the Biot-Savart law:
Where 


Plugging in values:
Compare your answer with the correct one above
A circular circuit is powered by a  battery. How will the magnetic field change if the battery is removed and placed in the opposite direction?
battery. How will the magnetic field change if the battery is removed and placed in the opposite direction?
A circular circuit is powered by a 
Reversing the battery will reverse the direction of the current. Using the right hand rule, it can be seen that this will also reverse the direction of the magnetic field. Since the magnitude of the current stays the same, the magnitude of the magnetic field will as well.
Reversing the battery will reverse the direction of the current. Using the right hand rule, it can be seen that this will also reverse the direction of the magnetic field. Since the magnitude of the current stays the same, the magnitude of the magnetic field will as well.
Compare your answer with the correct one above
A circular circuit is powered by a  battery. How will the magnetic field change if a second
battery. How will the magnetic field change if a second  battery is added in the same direction as the first?
battery is added in the same direction as the first?
A circular circuit is powered by a 

Based on the Biot-Savart law:

Doubling the voltage will double the current, which will double the magnetic field. The direction will stay the same.
Based on the Biot-Savart law:
Doubling the voltage will double the current, which will double the magnetic field. The direction will stay the same.
Compare your answer with the correct one above
If the north end of a magnetic points towards the geographic north pole, that means that the geographic north pole is a magnetic __________ pole.
If the north end of a magnetic points towards the geographic north pole, that means that the geographic north pole is a magnetic __________ pole.
Magnets will align themselves with the surrounding magnetic field. Thus, if the north pole of a magnet is pointing north, the direction of the magnetic field must be pointing north. Magnetic fields point towards magnetic south poles, so the geographic north pole is actually a magnetic south pole.
Magnets will align themselves with the surrounding magnetic field. Thus, if the north pole of a magnet is pointing north, the direction of the magnetic field must be pointing north. Magnetic fields point towards magnetic south poles, so the geographic north pole is actually a magnetic south pole.
Compare your answer with the correct one above
An infinitely long wire carries a current of  determine the magnitude of the magnetic field
determine the magnitude of the magnetic field  away.
away.
An infinitely long wire carries a current of 

Magnetic field of an infinitely long wire:

Where 
Plugging in values:


Magnetic field of an infinitely long wire:
Where
Plugging in values:
Compare your answer with the correct one above
Radius of moon: 
A loop of current carrying wire runs along the equator of the moon. Determine the magnetic field at the center of the loop if  are traveling through it
are traveling through it
Radius of moon:
A loop of current carrying wire runs along the equator of the moon. Determine the magnetic field at the center of the loop if 
Using

Plugging in values


Using
Plugging in values
Compare your answer with the correct one above
A circuit contains a  battery and a
battery and a  resistor in series. Determine the magnitude of the magnetic field outside of the loop
resistor in series. Determine the magnitude of the magnetic field outside of the loop  away from the wire.
away from the wire.
A circuit contains a 


Using

Converting  to
to  and plugging in values
and plugging in values

Determining current:





Using
Converting 

Determining current:
Compare your answer with the correct one above
How strong would a magnetic field need to be in order to make a particle with a mass of  and a charge of
and a charge of  move in a circular path with a speed of
move in a circular path with a speed of  and a radius of
and a radius of  ?
?
How strong would a magnetic field need to be in order to make a particle with a mass of 



For this question, we are being asked to determine the magnetic field necessary to make a particle of a given mass and charge to move in a circular path with a given speed and radius.
To begin with, we can realize that the particle will be moving in a circular path. Thus, there is going to be a centripetal force associated with this circular motion. Moreover, because we know the particle will be present in a magnetic field, we can infer that the magnetic force will be the source of the centripetal force. Thus, we can start by writing out the expression for each of these forces, and then setting them equal to one another.



Rearranging the above expression to isolate the term for magnetic field, we arrive at the following expression.

Now, we can plug in the values given to us in the question stem to solve for the magnetic field strength.


For this question, we are being asked to determine the magnetic field necessary to make a particle of a given mass and charge to move in a circular path with a given speed and radius.
To begin with, we can realize that the particle will be moving in a circular path. Thus, there is going to be a centripetal force associated with this circular motion. Moreover, because we know the particle will be present in a magnetic field, we can infer that the magnetic force will be the source of the centripetal force. Thus, we can start by writing out the expression for each of these forces, and then setting them equal to one another.
Rearranging the above expression to isolate the term for magnetic field, we arrive at the following expression.
Now, we can plug in the values given to us in the question stem to solve for the magnetic field strength.
Compare your answer with the correct one above
A proton traveling at 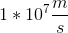 in a horizontal plane passes through an opening into a mass spectrometer with a uniform
in a horizontal plane passes through an opening into a mass spectrometer with a uniform  magnetic field directed upward. The particle then moves in a circular path through
magnetic field directed upward. The particle then moves in a circular path through  and crashes into the wall of the spectrometer adjacent to the entrance opening. How far down from the entrance is the proton when it crashes into the wall?
and crashes into the wall of the spectrometer adjacent to the entrance opening. How far down from the entrance is the proton when it crashes into the wall?
The proton’s mass is  and its electric charge is
and its electric charge is  .
.
A proton traveling at 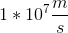


The proton’s mass is 


A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:

 is the charge,
is the charge,  is the particle speed, and
is the particle speed, and  is the magnetic field strength. This force is always directed perpendicular to the particle’s direction of travel at that moment, and thus acts as a centripetal force. This force is also given by the equation:
is the magnetic field strength. This force is always directed perpendicular to the particle’s direction of travel at that moment, and thus acts as a centripetal force. This force is also given by the equation:

We can set these two equations equal to one another, allowing us to solve for the radius of the arc.

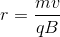
Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).

Twice this value is the lateral offset of its crash point from the entrance:


A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:



We can set these two equations equal to one another, allowing us to solve for the radius of the arc.
Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).
Twice this value is the lateral offset of its crash point from the entrance:
Compare your answer with the correct one above
A particle with a charge of  is moving at
is moving at  perpendicularly through a magnetic field with a strength of
perpendicularly through a magnetic field with a strength of  . What is the magnitude of the force on the particle?
. What is the magnitude of the force on the particle?
A particle with a charge of 


The equation for finding the force on a moving charged particle in a magnetic field is as follows:

Here,  is the force in Newtons,
is the force in Newtons,  is the charge in Coulombs,
is the charge in Coulombs,  is the velocity in
is the velocity in  , and
, and  is the magnetic field strength in Teslas.
is the magnetic field strength in Teslas.
Another way to write the equation without the cross-product is as follows:

Here,  is the angle between the particles velocity and the magnetic field.
is the angle between the particles velocity and the magnetic field.
For our problem, because theta is  ,
,  evaluates to 1, so we just need to perform multiplication.
evaluates to 1, so we just need to perform multiplication.



Therefore, the force on the particle is 0.3N.
The equation for finding the force on a moving charged particle in a magnetic field is as follows:
Here, 




Another way to write the equation without the cross-product is as follows:
Here, 
For our problem, because theta is 

Therefore, the force on the particle is 0.3N.
Compare your answer with the correct one above