Work, Energy, and Power - AP Physics 1
Card 0 of 20
A  ball starts rolling up a
ball starts rolling up a  incline at speed of
incline at speed of  . Using conservation of energy, find out how much work gravity does on the ball when it travels from the bottom to the maximum height.
. Using conservation of energy, find out how much work gravity does on the ball when it travels from the bottom to the maximum height.
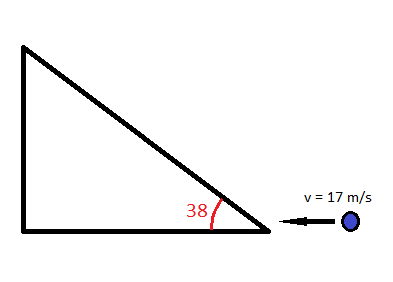
A 



The energies involved in this problem are kinetic and potential energy. Conservation of energy shows that the initial energies will be equal to the final energies.

Choosing the bottom of the incline to be the zero height, the ball starts out with kinetic energy and zero potential energy. When the ball reaches maximum height, its velocity is zero (zero kinetic energy). This simplifies our energy equation.

Isolate the height variable and use the given values to solve for the maximum height.



This is the vertical height. The work done by gravity is calculated as the product for force and distance.

The minus sign indicates that the force of gravity acts downward (negative direction).


The energies involved in this problem are kinetic and potential energy. Conservation of energy shows that the initial energies will be equal to the final energies.
Choosing the bottom of the incline to be the zero height, the ball starts out with kinetic energy and zero potential energy. When the ball reaches maximum height, its velocity is zero (zero kinetic energy). This simplifies our energy equation.
Isolate the height variable and use the given values to solve for the maximum height.
This is the vertical height. The work done by gravity is calculated as the product for force and distance.
The minus sign indicates that the force of gravity acts downward (negative direction).
Compare your answer with the correct one above
A  rubber ball is released from a height of
rubber ball is released from a height of  and is allowed to bounce repeatedly. Each time the ball strikes the ground, ten percent of the ball's kinetic energy is lost in the collision. What is the maximum height the ball will reach after hitting the ground four times?
and is allowed to bounce repeatedly. Each time the ball strikes the ground, ten percent of the ball's kinetic energy is lost in the collision. What is the maximum height the ball will reach after hitting the ground four times?
A 

Each time the ball bounces, 10% of the kinetic energy is lost. This means that after colliding with the ground, the ball has 90% of its previous potential energy at the top of its flight. To find the total energy after four bounces, we multiply the initial potential energy by  .
.
The initial potential energy is:



Use our exponential expression to find the remaining energy after four bounces.


Based on conservation of energy, we can find the height that the ball travels with this remaining kinetic energy



Each time the ball bounces, 10% of the kinetic energy is lost. This means that after colliding with the ground, the ball has 90% of its previous potential energy at the top of its flight. To find the total energy after four bounces, we multiply the initial potential energy by 
The initial potential energy is:
Use our exponential expression to find the remaining energy after four bounces.
Based on conservation of energy, we can find the height that the ball travels with this remaining kinetic energy
Compare your answer with the correct one above
A rollercoaster cart with a total mass of 1,000kg is at the top of a hill moving at  . Assuming no friction and neglecting air resistance, what is the speed of the cart when it reaches the bottom of the hill, 30m below?
. Assuming no friction and neglecting air resistance, what is the speed of the cart when it reaches the bottom of the hill, 30m below?
A rollercoaster cart with a total mass of 1,000kg is at the top of a hill moving at 
This question covers the conservation of energy:

From the problem statement, we know that the cart has both initial potential and kinetic energy. We can assume that there is no final potential energy. This means that there is final kinetic energy from the final velocity that we are trying to find.
After eliminating final potential energy, we can rewrite the equation as:

We can eliminate mass from the equation to get:

We are solving for final velocity, so rearranging, we get:

Values for each variable were given in the problem statement, so we can simply plug in these values to solve:

This question covers the conservation of energy:
From the problem statement, we know that the cart has both initial potential and kinetic energy. We can assume that there is no final potential energy. This means that there is final kinetic energy from the final velocity that we are trying to find.
After eliminating final potential energy, we can rewrite the equation as:
We can eliminate mass from the equation to get:
We are solving for final velocity, so rearranging, we get:
Values for each variable were given in the problem statement, so we can simply plug in these values to solve:
Compare your answer with the correct one above
A roller coaster of mass 500kg is at its highest point in a loop traveling at a velocity of  . The loop is 15 meters tall. Assuming 5000J of energy is lost between the highest and lowest points of the loop, how fast is the roller coaster traveling when it reaches the lowest point of the loop?
. The loop is 15 meters tall. Assuming 5000J of energy is lost between the highest and lowest points of the loop, how fast is the roller coaster traveling when it reaches the lowest point of the loop?
A roller coaster of mass 500kg is at its highest point in a loop traveling at a velocity of 
This problem covers the conservation of energy (including friction):

The only term we can eliminate is final potential energy:

Expanding each of the terms, we get:

We can rearrange this to solve for final velocity:

Many students will look at this and feel that the equation has just become more complex or harder to follow. However, the idea behind this is to reduce calculation errors. By doing all of your subsitutions of variables and rearrangements of the equations before plugging in your values, you only have to do a single calculation. This greatly reduces the frequency of silly calculation errors. Furthermore, it tends to make it much easier to follow your units in case you need to troubleshoot the problem.
Now, plugging in all of our values, we get:



This problem covers the conservation of energy (including friction):
The only term we can eliminate is final potential energy:
Expanding each of the terms, we get:
We can rearrange this to solve for final velocity:
Many students will look at this and feel that the equation has just become more complex or harder to follow. However, the idea behind this is to reduce calculation errors. By doing all of your subsitutions of variables and rearrangements of the equations before plugging in your values, you only have to do a single calculation. This greatly reduces the frequency of silly calculation errors. Furthermore, it tends to make it much easier to follow your units in case you need to troubleshoot the problem.
Now, plugging in all of our values, we get:
Compare your answer with the correct one above
A group of ten friends, each of mass 50kg, want to test the strength of a trampoline. At their highest jump, each friend is 2m above the trampoline. They all land on the trampoline at the same time and decelerate at a constant rate to a point of zero velocity over a period of 0.5s. The trampoline has a threshold of 5000N, above which it breaks. Do the friends succeed in breaking their trampoline?
Neglect air resistance and the distance the trampoline sags as a result of the friends landing.

A group of ten friends, each of mass 50kg, want to test the strength of a trampoline. At their highest jump, each friend is 2m above the trampoline. They all land on the trampoline at the same time and decelerate at a constant rate to a point of zero velocity over a period of 0.5s. The trampoline has a threshold of 5000N, above which it breaks. Do the friends succeed in breaking their trampoline?
Neglect air resistance and the distance the trampoline sags as a result of the friends landing.
According to the problem statement, we can treat the friends as a single mass of 500kg. We can use the expression for conservation of energy to calculate the velocity as they hit the trampoline.

If we take the initial state to be when the friends are at their highest point and the final state to be when the friends hit the trampoline, we can rewrite:

Substituting in expressions:

Rearranging for velocity:

Plugging in our values:

The statement says that the friends decelerate from this velocity to zero over a period of 0.5 seconds. Therefore, we can write:

We can use this to calculate the force that the trampoline is exerting on the friends:

This is above the threshold of 5000 N, so the trampoline does break.
According to the problem statement, we can treat the friends as a single mass of 500kg. We can use the expression for conservation of energy to calculate the velocity as they hit the trampoline.
If we take the initial state to be when the friends are at their highest point and the final state to be when the friends hit the trampoline, we can rewrite:
Substituting in expressions:
Rearranging for velocity:
Plugging in our values:
The statement says that the friends decelerate from this velocity to zero over a period of 0.5 seconds. Therefore, we can write:
We can use this to calculate the force that the trampoline is exerting on the friends:
This is above the threshold of 5000 N, so the trampoline does break.
Compare your answer with the correct one above
For a baseball field, the distance between home plate and the center field wall is about  and the wall is
and the wall is  tall. If a player hits the ball at a level of
tall. If a player hits the ball at a level of  off the ground, an angle of
off the ground, an angle of  above the horizontal, and a velocity of
above the horizontal, and a velocity of  , what is the total velocity of the ball as it passes over the center field wall at a height of
, what is the total velocity of the ball as it passes over the center field wall at a height of  ?
?
Neglect air resistance and assume 
For a baseball field, the distance between home plate and the center field wall is about 





Neglect air resistance and assume
There are two ways to solve this problem. The first uses the concept of conservation of energy, and the second uses kinematics. We'll go through both methods, as you should be comfortable using either one, as some problems won't have the ability to be easily solved using two different methods.
Method 1: Conservation of Energy
Note: The only reason we can use this method is because we know the height at which the ball crosses over the center field wall. Without that height, we would have to do method 2.
We will first split the initial velocity of the ball into its components:


Since we are neglecting air resistance, the x-component stays constant. Therefore we can say:

We can find the final y-componenet using our conservation of energy equation:

Substituting in our expressions:

Canceling out mass and rearranging for final velocity:


Note that this is one of the big five kineamtics equations with which you should be familiar. Plugging in our values, we get:


Now that we have the components, we can combine them to get the final velocity:


Method 2: Kinematics
We start off the same way by separating the velocities into their components:


Since we are neglecting air resistance, the x-component stays constant. Therefore we can say:

We also know how far the ball travels horizontally, so we can find out long it takes to cover that distance:

We can then use this time to find out the final vertical velocity:

The acceleration is subtracted because the acceleration is technically negative.

The velocity is negative because the ball is now traveling back downward. We can now combine the component velocities into the final velocity of the ball:


There are two ways to solve this problem. The first uses the concept of conservation of energy, and the second uses kinematics. We'll go through both methods, as you should be comfortable using either one, as some problems won't have the ability to be easily solved using two different methods.
Method 1: Conservation of Energy
Note: The only reason we can use this method is because we know the height at which the ball crosses over the center field wall. Without that height, we would have to do method 2.
We will first split the initial velocity of the ball into its components:
Since we are neglecting air resistance, the x-component stays constant. Therefore we can say:
We can find the final y-componenet using our conservation of energy equation:
Substituting in our expressions:
Canceling out mass and rearranging for final velocity:
Note that this is one of the big five kineamtics equations with which you should be familiar. Plugging in our values, we get:
Now that we have the components, we can combine them to get the final velocity:
Method 2: Kinematics
We start off the same way by separating the velocities into their components:
Since we are neglecting air resistance, the x-component stays constant. Therefore we can say:
We also know how far the ball travels horizontally, so we can find out long it takes to cover that distance:
We can then use this time to find out the final vertical velocity:
The acceleration is subtracted because the acceleration is technically negative.
The velocity is negative because the ball is now traveling back downward. We can now combine the component velocities into the final velocity of the ball:
Compare your answer with the correct one above
Consider the following system:
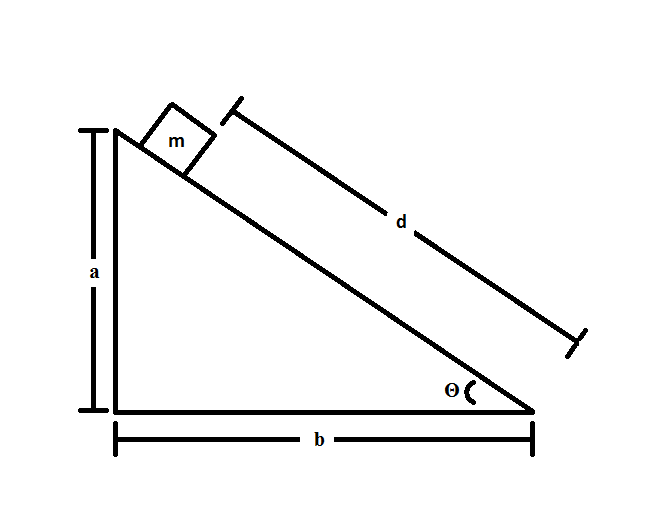
The coefficient of friction between the block and the slope is  . The block has a mass of
. The block has a mass of  and a constant velocity. If the height of the slope is
and a constant velocity. If the height of the slope is  , how much work is done by friction over the distance
, how much work is done by friction over the distance  ?
?

Consider the following system:

The coefficient of friction between the block and the slope is 



First, we'll write out the equation for conservation of energy:

The velocity of the block is constant, so kinetic energies will cancel out. Furthermore, we can remove final potential energy if we say that the final height is 0m. Therefore, we get:

Substituting in the expression for potential energy, we get:

Note that this problem cannot be solved by using the force of gravity and force of friction because we do not know the angle of the slope.
First, we'll write out the equation for conservation of energy:
The velocity of the block is constant, so kinetic energies will cancel out. Furthermore, we can remove final potential energy if we say that the final height is 0m. Therefore, we get:
Substituting in the expression for potential energy, we get:
Note that this problem cannot be solved by using the force of gravity and force of friction because we do not know the angle of the slope.
Compare your answer with the correct one above
John jumps upwards off the ground with an initial velocity of  . What is the maximum height he can reach?
. What is the maximum height he can reach?

John jumps upwards off the ground with an initial velocity of 
While this problem can be solved by using kinematic equations for motion with constant acceleration, the simplest solution comes from using conservation of energy. Immediately after John leaves the ground, he has a potential energy of 0J and a kinetic energy given by his initial velocity. So we have that John's initial energy is given by:

When John reaches the highest point, his velocity must be zero since this would be the point where he stops for an instant just before start falling down. Therefore, at his highest point John has a kinetic energy of 0J and a potential energy given by gravity

So we have that at his highest point, John's energy is given by:

Where  is the height above the ground.
is the height above the ground.
Therefore, by conservation of energy, we have:



While this problem can be solved by using kinematic equations for motion with constant acceleration, the simplest solution comes from using conservation of energy. Immediately after John leaves the ground, he has a potential energy of 0J and a kinetic energy given by his initial velocity. So we have that John's initial energy is given by:
When John reaches the highest point, his velocity must be zero since this would be the point where he stops for an instant just before start falling down. Therefore, at his highest point John has a kinetic energy of 0J and a potential energy given by gravity
So we have that at his highest point, John's energy is given by:
Where 
Therefore, by conservation of energy, we have:
Compare your answer with the correct one above
A pebble is dropped from a height of  . What is its speed
. What is its speed  before it hits the ground? Disregard the effects of air resistance.
before it hits the ground? Disregard the effects of air resistance.

A pebble is dropped from a height of 

Energy in a system must be conserved, and the energy in the falling pebble is either potential or kinetic:

Potential energy is represented by the  terms.
terms.
Kinetic energy is represented by the  terms.
terms.
At the exact moment the pebble is released, its stationary, so 





Energy in a system must be conserved, and the energy in the falling pebble is either potential or kinetic:
Potential energy is represented by the 
Kinetic energy is represented by the 
At the exact moment the pebble is released, its stationary, so
Compare your answer with the correct one above

Consider a case where a block is sitting at rest atop a frictionless semicircle with radius  as shown in the given figure. If the block were to begin sliding to the right, at what height above the ground would the block lose contact with the semicircle?
as shown in the given figure. If the block were to begin sliding to the right, at what height above the ground would the block lose contact with the semicircle?

Consider a case where a block is sitting at rest atop a frictionless semicircle with radius 
To begin with, we'll need to approach this problem from two angles. First, we'll need to consider the changes in energy that occur to the block as it slides from its initial position at rest to the point at which it falls off. Since we are told that the semicircle is frictionless, then we can expect the energy in the block-semicircle system to remain constant - the total mechanical energy will not change. Additionally, since the block is moving in a circular motion, we'll need to consider the centripetal force acting upon the block.
So, we need to find an expression that relates the initial energy to the final energy. In doing so, we'll need to consider both the gravitational potential energy of the block, as well as its kinetic energy. Initially, the block has potential energy but it does not have kinetic energy because it is at rest. Upon falling off the semicircle, the block will have both potential and kinetic energy.



Because the block is initially at the top of the semicircle, this starting height is equal to the radius of the semicircle. Once it slides down, it will be at a height that is less than its initial height. We can relate the height at any given point along the semicircle to its radius by employing trigonometry as shown below:



Plug in these expressions for height into the above expressions for energy.

Solve for velocity.

But we also need to approach this problem from another perspective. Since the block is moving in a circular motion, we know that we will be dealing with a centripetal force. Thus, it will be useful for us to consider the forces acting upon the block as it slides down the semicircle.
First, let's consider the forces acting parallel to the surface of the semicircle. Since the surface is frictionless, we won't have to worry about any frictional forces as the block slides. That means that our only force in this direction is the gravitational component that acts tangentially to the surface. Fortunately, we will not need this value to find our answer.
Now, let's consider the forces acting perpendicularly to the surface, or in other words, radially. For one, we have the radial component of the gravitational force, which points towards the center of the circle. Acting in the opposite direction to this we have the normal force. The difference in these two values is what provides the centripetal force that keeps the block on the surface.



In order to identify the height at which the block loses contact with the surface, we need to realize that this will happen once the radial component of the gravitational force can no longer provide an adequate centripetal force to keep the block attached. In such a situation, the block will lose contact with the surface and the normal force will reduce to zero. We will then have:

Now, if we substitute the expression for velocity that we derived from considering energy into the expression for centripetal force, we obtain:

By canceling common terms and rearranging, we obtain the following expression:





To begin with, we'll need to approach this problem from two angles. First, we'll need to consider the changes in energy that occur to the block as it slides from its initial position at rest to the point at which it falls off. Since we are told that the semicircle is frictionless, then we can expect the energy in the block-semicircle system to remain constant - the total mechanical energy will not change. Additionally, since the block is moving in a circular motion, we'll need to consider the centripetal force acting upon the block.
So, we need to find an expression that relates the initial energy to the final energy. In doing so, we'll need to consider both the gravitational potential energy of the block, as well as its kinetic energy. Initially, the block has potential energy but it does not have kinetic energy because it is at rest. Upon falling off the semicircle, the block will have both potential and kinetic energy.
Because the block is initially at the top of the semicircle, this starting height is equal to the radius of the semicircle. Once it slides down, it will be at a height that is less than its initial height. We can relate the height at any given point along the semicircle to its radius by employing trigonometry as shown below:

Plug in these expressions for height into the above expressions for energy.
Solve for velocity.
But we also need to approach this problem from another perspective. Since the block is moving in a circular motion, we know that we will be dealing with a centripetal force. Thus, it will be useful for us to consider the forces acting upon the block as it slides down the semicircle.
First, let's consider the forces acting parallel to the surface of the semicircle. Since the surface is frictionless, we won't have to worry about any frictional forces as the block slides. That means that our only force in this direction is the gravitational component that acts tangentially to the surface. Fortunately, we will not need this value to find our answer.
Now, let's consider the forces acting perpendicularly to the surface, or in other words, radially. For one, we have the radial component of the gravitational force, which points towards the center of the circle. Acting in the opposite direction to this we have the normal force. The difference in these two values is what provides the centripetal force that keeps the block on the surface.
In order to identify the height at which the block loses contact with the surface, we need to realize that this will happen once the radial component of the gravitational force can no longer provide an adequate centripetal force to keep the block attached. In such a situation, the block will lose contact with the surface and the normal force will reduce to zero. We will then have:
Now, if we substitute the expression for velocity that we derived from considering energy into the expression for centripetal force, we obtain:
By canceling common terms and rearranging, we obtain the following expression:
Compare your answer with the correct one above

A cart, rolling to the right without friction, encounters a fixed ramp as shown in the figure. The mass of the cart is not known, but its velocity is  . When the cart comes to rest on the ramp, what will its height above the floor be?
. When the cart comes to rest on the ramp, what will its height above the floor be?

A cart, rolling to the right without friction, encounters a fixed ramp as shown in the figure. The mass of the cart is not known, but its velocity is 
This problem is best solved using mechanical energy conservation. All of the cart's kinetic energy  will be converted into gravitational potential energy
will be converted into gravitational potential energy  at the instant the cart comes to rest. Set these equations equal to each other. We find that mass is a common term, and gets cancelled out.
at the instant the cart comes to rest. Set these equations equal to each other. We find that mass is a common term, and gets cancelled out.



Solve for height.



This problem is best solved using mechanical energy conservation. All of the cart's kinetic energy 

Solve for height.
Compare your answer with the correct one above

Suppose that a block of mass  slides down a frictionless halfpipe from a starting height
slides down a frictionless halfpipe from a starting height  and collides with a second block of mass
and collides with a second block of mass  at the bottom. If the two blocks then slide together, which of the following expressions gives the maximum height
at the bottom. If the two blocks then slide together, which of the following expressions gives the maximum height  that these two blocks will reach before sliding back down?
that these two blocks will reach before sliding back down?

Suppose that a block of mass 



To begin with, we'll need to consider the energy of the blocks initially and right before the collision. Initially, block 1 is starting at some height and therefore has gravitational potential energy. Block 2 is initially not moving and is at the bottom of the half pipe, therefore it does not have any energy.

We'll also need to consider the energy of the blocks the instant right before the collision. In such a situation, all of the gravitational potential energy of block 1 has been converted into kinetic energy. Block 2, just as before, is at rest at the bottom of the half pipe and thus does not have any energy.

From these equations and knowing that energy is conserved, we can solve for the velocity of block 1 just before the collision.




In addition to considering the energy associated with the collision, it's also important for us to consider the momentum before and after the collision. In the instant right before the collision, block 1 has a velocity which we calculated above, while block 2 is at rest. After the collision, we're told in the question stem that the two blocks will move together. And due to conservation of momentum, we can relate the initial and final momentum as equal to each other.

Now solve for the final velocity of the two-block system.

Plug in the value for the velocity of block 1.

The above expression represents the velocity of the two-block system right after the collision. Knowing this, we can find an expression for the energy of both blocks the instant after the collision, and then relate this value to the final energy of both blocks as they ascend.
The instant after the collision, both blocks will be at the bottom of the halfpipe and will thus have no gravitational potential energy. However, the two blocks will have a certain velocity, which we calculated above. Thus, the two blocks will have kinetic energy. As the two blocks ascend and reach their maximum height, all of their kinetic energy will be converted into gravitational potential energy.


Now, plug in the final velocity expression that we calculated above for the two blocks.



To begin with, we'll need to consider the energy of the blocks initially and right before the collision. Initially, block 1 is starting at some height and therefore has gravitational potential energy. Block 2 is initially not moving and is at the bottom of the half pipe, therefore it does not have any energy.
We'll also need to consider the energy of the blocks the instant right before the collision. In such a situation, all of the gravitational potential energy of block 1 has been converted into kinetic energy. Block 2, just as before, is at rest at the bottom of the half pipe and thus does not have any energy.
From these equations and knowing that energy is conserved, we can solve for the velocity of block 1 just before the collision.
In addition to considering the energy associated with the collision, it's also important for us to consider the momentum before and after the collision. In the instant right before the collision, block 1 has a velocity which we calculated above, while block 2 is at rest. After the collision, we're told in the question stem that the two blocks will move together. And due to conservation of momentum, we can relate the initial and final momentum as equal to each other.
Now solve for the final velocity of the two-block system.
Plug in the value for the velocity of block 1.
The above expression represents the velocity of the two-block system right after the collision. Knowing this, we can find an expression for the energy of both blocks the instant after the collision, and then relate this value to the final energy of both blocks as they ascend.
The instant after the collision, both blocks will be at the bottom of the halfpipe and will thus have no gravitational potential energy. However, the two blocks will have a certain velocity, which we calculated above. Thus, the two blocks will have kinetic energy. As the two blocks ascend and reach their maximum height, all of their kinetic energy will be converted into gravitational potential energy.
Now, plug in the final velocity expression that we calculated above for the two blocks.
Compare your answer with the correct one above
A 50kg block is released from its resting position at a height of 10m from the ground. If we neglect air resistance, what is the block's total energy at a height of 4m from the ground?
A 50kg block is released from its resting position at a height of 10m from the ground. If we neglect air resistance, what is the block's total energy at a height of 4m from the ground?
To solve this problem, we'll need to consider the initial energy of the block. Since it is starting from rest, it will not have any kinetic energy. Rather, all of its energy will be in the form of gravitational potential energy.

Once the block is released from its resting position, it will begin to fall towards the ground. As it falls, it will lose potential energy, but it will gain kinetic energy as it picks up speed. What's important to realize is that because we are neglecting air resistance, we have a situation in which total mechanical energy is conserved. Therefore, as the block loses potential energy during its fall, it will gain an exactly equal amount of kinetic energy. Therefore, no matter where the block is during its fall, its total mechanical energy will be the same! Keeping this in mind, we can equate the total mechanical energy of the block at any point during its fall with its initial potential energy, which we calculated above.
To solve this problem, we'll need to consider the initial energy of the block. Since it is starting from rest, it will not have any kinetic energy. Rather, all of its energy will be in the form of gravitational potential energy.
Once the block is released from its resting position, it will begin to fall towards the ground. As it falls, it will lose potential energy, but it will gain kinetic energy as it picks up speed. What's important to realize is that because we are neglecting air resistance, we have a situation in which total mechanical energy is conserved. Therefore, as the block loses potential energy during its fall, it will gain an exactly equal amount of kinetic energy. Therefore, no matter where the block is during its fall, its total mechanical energy will be the same! Keeping this in mind, we can equate the total mechanical energy of the block at any point during its fall with its initial potential energy, which we calculated above.
Compare your answer with the correct one above
Terry believes he can throw a ball vertically and hit a target  above himself. If the ball weighs
above himself. If the ball weighs  , how fast must it be traveling when it leaves his hand to just reach the target? Neglect air resistance.
, how fast must it be traveling when it leaves his hand to just reach the target? Neglect air resistance.

Terry believes he can throw a ball vertically and hit a target 

This problem deals with both potential energy and kinetic energy.
Potential energy is expressed as:

Kinetic energy is expressed as:

Energy must be conserved, so set up the following equation:

The initial height can be treated as zero, as can the final velocity. Plug in these zero values into the above equation.

Solve for  , the initial velocity the ball needs in order to reach a maximum height of
, the initial velocity the ball needs in order to reach a maximum height of  .
.




This problem deals with both potential energy and kinetic energy.
Potential energy is expressed as:
Kinetic energy is expressed as:
Energy must be conserved, so set up the following equation:
The initial height can be treated as zero, as can the final velocity. Plug in these zero values into the above equation.
Solve for 

Compare your answer with the correct one above
You are in Paris, France, holding on to a tennis ball of mass  .
.
You throw it straight up. It leaves your hand two meters above the ground at a speed of  .
.
What is the maximum height above the ground the ball obtains?
You may use as your acceleration.
as your acceleration.
You are in Paris, France, holding on to a tennis ball of mass 
You throw it straight up. It leaves your hand two meters above the ground at a speed of 
What is the maximum height above the ground the ball obtains?
You may use
We will use conservation of energy to help us.
We will treat our initial situation as the moment the ball left the hand, and the final situation as the ball at the maximum height.


Mass cancels out

 will be zero at our maximum height
will be zero at our maximum height

Rearranging our equatin to solve for 

We then plug in our values


We will use conservation of energy to help us.
We will treat our initial situation as the moment the ball left the hand, and the final situation as the ball at the maximum height.
Mass cancels out

Rearranging our equatin to solve for
We then plug in our values
Compare your answer with the correct one above
Assume no mechanical energy is lost in the following question.
An object with mass 6kg starts at a height of 35m above the earth's surface with an upward velocity of  . Determine the total energy of the object once it reaches 10m above the earth's surface.
. Determine the total energy of the object once it reaches 10m above the earth's surface.

Assume no mechanical energy is lost in the following question.
An object with mass 6kg starts at a height of 35m above the earth's surface with an upward velocity of 
Since total energy can be determined in this situation as:

In our case,

Here,  is the mass of the object and
is the mass of the object and  is its velocity
is its velocity

Here,  is the mass of the object,
is the mass of the object,  is the gravitational constant, and
is the gravitational constant, and  is the distance from the datum (where the potential energy is considered to be zero). During the process of the ball falling down, the total energy of the system is conserved, so at
is the distance from the datum (where the potential energy is considered to be zero). During the process of the ball falling down, the total energy of the system is conserved, so at  , the ball will have the same total energy as it does at
, the ball will have the same total energy as it does at  .
.
At this height, the ball has  ,
,  ,
,  , and
, and 
Plug in known values and solve.


Since total energy can be determined in this situation as:
In our case,
Here, 

Here, 




At this height, the ball has 


Plug in known values and solve.
Compare your answer with the correct one above
An archer pulls back on the string of a bow to  away from equilibrium. The bow has a resistance constant of
away from equilibrium. The bow has a resistance constant of  . The mass of the arrow is
. The mass of the arrow is  . What is the velocity of the arrow when the bowstring is released just as the string passes through the equilibrium point?
. What is the velocity of the arrow when the bowstring is released just as the string passes through the equilibrium point?
An archer pulls back on the string of a bow to 


When the bowstring is drawn back, it acts like a spring and has potential energy:

When the string is released, the arrow turns all of that potential energy into kinetic energy:

Using conservation of energy to solve for velocity:



One thing to remember is that the mass of the arrow was given in grams, but kilograms are needed:


When the bowstring is drawn back, it acts like a spring and has potential energy:
When the string is released, the arrow turns all of that potential energy into kinetic energy:
Using conservation of energy to solve for velocity:
One thing to remember is that the mass of the arrow was given in grams, but kilograms are needed:
Compare your answer with the correct one above
A  block is released from rest on a frictionless ramp inclined at an angle of
block is released from rest on a frictionless ramp inclined at an angle of  with respect to the horizontal. Using conservation of energy methods, calculate the final velocity of the block if it slides a distance of
with respect to the horizontal. Using conservation of energy methods, calculate the final velocity of the block if it slides a distance of  down the incline.
down the incline.
A 


To solve this problem, we must look at the total energy of the system at two different times: at the beginning before the motion starts, and at the end of the incline. From there, we can use the conservation of energy to solve for the speed of the object at the bottom of the incline.


To solve this problem, we must look at the total energy of the system at two different times: at the beginning before the motion starts, and at the end of the incline. From there, we can use the conservation of energy to solve for the speed of the object at the bottom of the incline.
Compare your answer with the correct one above
A spring with a spring constant of 1000 N/m is compressed a distance of 30 cm. A projectile of mass 2 kg is placed on the end of the spring. Assume the spring is then tilted 45 degrees away from the vertical(striaght up) and the ball is then launched by the spring. How fast is the ball traveling when it reaches a height of 1 meter? Assume the height of the spring is neglegible.
A spring with a spring constant of 1000 N/m is compressed a distance of 30 cm. A projectile of mass 2 kg is placed on the end of the spring. Assume the spring is then tilted 45 degrees away from the vertical(striaght up) and the ball is then launched by the spring. How fast is the ball traveling when it reaches a height of 1 meter? Assume the height of the spring is neglegible.
There are three main quantities that suggest using conservation of energy: speed, height, and the compression of a spring. Reason being, these are the main terms that come up in the equations to describe these particular energies.
Spring Potential Energy: 
Gravitational Potential Energy: 
Kinetic Energy: 
This principle we start from is the work-energy therorem that states the change in energy of a system is equal to the amount of non-conservative ork the system does on the enviornment.

Non conservative work typically comes in the form of friction. There are more types of non conservative forces, but they can become nebulous and they are often not dealt with in problems such as these. Considering friction is not a part of this problem we can simplify the above equation to:

This also implies the final energy is equal to the initial energy:

Now we can write down every term that we deal with in the problem.

I am chosing the initial location to be when the spring is compressed and the ball is not in motion. The final location is where the ball is 1 meter from the ground. Eliminate terms that are zero:
GPE initial is zero because typically the zero of the problem is chosen at the lowest height(h=0). KE initial is zero because the ball is not in motion yet. SPE finial is zero because we assume the spring expanded back to it's equilibrium position after launching the ball. So we are left with:

We can conceptually understand this equation as the energy held in the compressed spring has been transfered into displacing the ball upwards the the gravitiational field, and the energy also went it to giving the ball motion. Lets now show the variables at play:

We now can solve for the speed of the ball:

If you don't see how I solved for  , ask someone for help with the algebra. Plugging into this equation we see the speed at 1 meters is
, ask someone for help with the algebra. Plugging into this equation we see the speed at 1 meters is  .
.
There are three main quantities that suggest using conservation of energy: speed, height, and the compression of a spring. Reason being, these are the main terms that come up in the equations to describe these particular energies.
Spring Potential Energy:
Gravitational Potential Energy:
Kinetic Energy:
This principle we start from is the work-energy therorem that states the change in energy of a system is equal to the amount of non-conservative ork the system does on the enviornment.
Non conservative work typically comes in the form of friction. There are more types of non conservative forces, but they can become nebulous and they are often not dealt with in problems such as these. Considering friction is not a part of this problem we can simplify the above equation to:
This also implies the final energy is equal to the initial energy:
Now we can write down every term that we deal with in the problem.
I am chosing the initial location to be when the spring is compressed and the ball is not in motion. The final location is where the ball is 1 meter from the ground. Eliminate terms that are zero:
GPE initial is zero because typically the zero of the problem is chosen at the lowest height(h=0). KE initial is zero because the ball is not in motion yet. SPE finial is zero because we assume the spring expanded back to it's equilibrium position after launching the ball. So we are left with:
We can conceptually understand this equation as the energy held in the compressed spring has been transfered into displacing the ball upwards the the gravitiational field, and the energy also went it to giving the ball motion. Lets now show the variables at play:
We now can solve for the speed of the ball:
If you don't see how I solved for 

Compare your answer with the correct one above
How much energy is lost to the environment for a ball weighing 15kg thrown up from a height of 30m at  , that comes down at a speed of
, that comes down at a speed of  at 25m above the ground?
at 25m above the ground?

How much energy is lost to the environment for a ball weighing 15kg thrown up from a height of 30m at 

We know that the total energy lost to the environment is equal to the negative change in mechanical energy. This is because all of the energy lost to the environment came from the decrease in mechanical energy.

Change in mechanical energy  is given as:
is given as:

Where  is change in kinetic energy and
is change in kinetic energy and  is change in potential energy.
is change in potential energy.
First determine the change in kinetic energy:

Where  is the mass,
is the mass,  is the final velocity and
is the final velocity and  is the initial velocity.
is the initial velocity.
In this case, since the ball is going at the same speed initially and terminally  , and has not changed its mass:
, and has not changed its mass:

Now, let's determine the change in potential energy:

Where  is the mass,
is the mass,  is the gravitational constant,
is the gravitational constant,  is the final height above the ground and
is the final height above the ground and  is the initial height above the ground.
is the initial height above the ground.
We initially started out 30m above the ground and came down to 25m above the ground. The mass is unchanged at 15kg, and the gravitational constant is given. Plug these values into the equation for change in potential energy:


Therefore,

Since

We know that the total energy lost to the environment is equal to the negative change in mechanical energy. This is because all of the energy lost to the environment came from the decrease in mechanical energy.
Change in mechanical energy 
Where 

First determine the change in kinetic energy:
Where 


In this case, since the ball is going at the same speed initially and terminally 
Now, let's determine the change in potential energy:
Where 



We initially started out 30m above the ground and came down to 25m above the ground. The mass is unchanged at 15kg, and the gravitational constant is given. Plug these values into the equation for change in potential energy:
Therefore,
Since
Compare your answer with the correct one above