Kinetic Energy - AP Physics 1

Card 0 of 20

Question

A bungie jumper of mass is attached to a bungie with a constant of $100 \frac{N}{m}$ . The unstretched length of the bungie is . What is the maxmimum velocity of the jumper?

$g = 10\frac{m}{s^2}$

Answer

Think about this scenario practically. After the jumper jumps, he will begin accelerating at a rate of $10\frac{m}{s^2}$ . This rate will stay constant until the bungie cord begins to stretch. At this point, the jumper has traveled a distance of . The rate of acceleration will now decrease and ultimately reach a rate of $0 \frac{m}{s^2}$ . This is the point at which the force from the bungie cord is equal and opposite to the force of gravity. This is also the point at which the jumper is traveling at his or her maxmium velocity. With all of this in mind, let's start writing expressions for the scenario.

The main expression we will use will be the one for conservation of energy:

Plugging in our expressions for these variables and removing initial kinetic energy, we get:

$mgh_i = \frac{1}{2}kx^2+\frac{1}{2}mv_f^2$

Rearranging for velocity:

$v_f = \sqrt{2gh_i - \frac{kx^2}{m}}$

We simply need to find the height distance between the jumper's initial position and the position at which the jumper is traveling at his or her greatest velocity. As previously mentioned, the point of highest velocity is the point at which the force from the bungie cord is equal and opposite to the force of gravity:

$F_{net} = 0$

Rearranging for , we get:

$x = \frac{ma}{k}$

This is the distance that the bungie is stretched. Therefore, we can say that the total height distance between the initial and final state is the length of the unstretched bungie cord plus the distance the cord has stretched:

$h_i = l + x = l + \frac{ma}{k}$

Plugging this back into the equation for final velocity, we get:

$v_f = \sqrt{2g(l+\frac{ma}{k})-\frac{kx^2}{m}}$

We have values for all of our variables, so we can simply solve for the final velocity:

$v_f = \sqrt{2(10\frac{m}{s^2})\left ( 15m+\frac{(50kg)(10\frac{m}{s^2})}{100\frac{N}{m}}\right )-\frac{(100\frac{N}{m})(5m)^2}{50kg}}$

$v_f = \sqrt{2(10\frac{m}{s^2})(20m)-50\frac{m^2}{s^2}} = 18.7\frac{m}{s}$

Compare your answer with the correct one above

Question

A few friends are having a water balloon fight. One friend throws a balloon of mass at another friend on a ledge above him. If the balloon hits the second friend at a rate of $3\frac{m}{s}$ , how much energy did the first friend expend throwing the balloon?

$g=10\frac{m}{s^2}$

Answer

We can use the equation for conservation of energy to solve this problem:

If we set the original height to , we can then remove initital potential energy from the equation. Furthermore, the intital kinetic energy will be the amount of energy that the first friend used to throw the balloon. Substituting in expressions for the final variables, we get:

$K_i=mgh_f+\frac{1}{2}mv_f^2$

We know all of the variables, allowing us to solve:

$K_i = (2kg)(10\frac{m}{s^2})(5m)+\frac{1}{2}(2kg)(3\frac{m}{s})^2$

Compare your answer with the correct one above

Question

A man of mass is going skydiving. After jumping out of the plane, he travels a distance of before reaching a terminal velocity of $75\frac{m}{s}$ . How much work did air resistance do on the diver before he reached terminal velocity?

$g = 10\frac{m}{s^2}$

Answer

We can use the equation for conservation of energy to solve this problem:

Here, is the work done by air resistance.

If we say that the height at which the diver reaches terminal velocity is equal to 0, we can rewrite:

Plugging in expressions for potential and kinetic energy and rearranging for air resistance, we get:

$AR = mgh - \frac{1}{2}mv^2$

We have values for each variable, allowing us to solve:

$AR = (100kg)(10\frac{m}{s^2})(500m) - \frac{1}{2}(100kg)(75\frac{m}{s})$

Compare your answer with the correct one above

Question

Consider the following system:

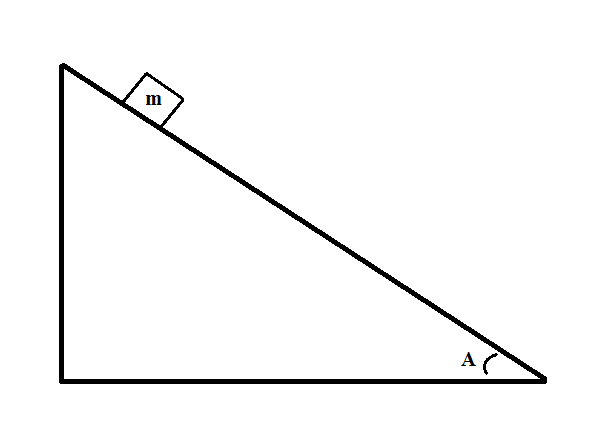
There is no friction between the block and plane, and the angle measures $20^{\circ}$ . If the block starts from rest, what is the velocity of the block after it travels down of the slope?

$g = 10\frac{m}{s^2}$

Answer

We can use the equation for conservation of energy to solve this problem:

If we designate the final height to be zero, we can eliminate final potential energy and initial kinetic energy, since the block starts at rest. Therefore, we get:

Substitute expressions for each type of energy:

$mgh_i = \frac{1}{2}mv_f^2$

Eliminate mass and rearrange for final velocity:

$v_f = \sqrt{2gh_i}$

We don't know what the initial height is at this point. We do know what the distance traveled down the slope and angle are, so we can figure out the distance traveled using the following equation:

$sin(\theta)=\frac{h_i}{d}$

Rearranging for initial height, we get:

$h_i = dsin(\theta) = (20m)sin(20^{\circ})$

Now we have all of the information we need to solve for the final velocity:

$v_f = \sqrt{2(10\frac{m}{s^2})(6.84m)} = 11.7\frac{m}{s}$

Compare your answer with the correct one above

Question

An object of mass moves with velocity . How fast must an object of mass move in order to have the same kinetic energy of the object of mass ?

Answer

Kinetic energy is equal to $\frac{1}{2}mv^2$ . The object of mass and velocity therefore has kinetic energy equal to $\frac{1}{2}mv^2$ . Let's let the object of mass have velocity $v_{4m}$ . Therefore, its kinetic energy is $\frac{1}{2}mv_{4m}^2$ . We want to find $v_{4m}$ such that the two objects to have the same kinetic energy, so we can equate their two kinetic energies. $\frac{1}{2}mv^2=\frac{1}{2}4mv_{4m}^2$

$v^2=4v_{4m}^2$

$\frac{v^2}{4}=v_{4m}^2$

$\frac{v^2}{2}=v_{4m}$

Compare your answer with the correct one above

Question

Two objects, one of mass, , and the other of mass, , are traveling at constant velocity along a frictionless surface. The lighter object travels at , while the heavier travels at . An opposing horizontal force acts upon both objects equally, and brings them to rest. Which object takes longer to slow down, and why?

Answer

Examining the formula for kinetic energy will allow us to compare the two objects. The formula, $KE = .5mv^{2}$ , shows us that velocity has a higher influence in the calculation of Kinetic Energy than mass does. The velocity of the lighter object is double that of the heavier object, and because of the velocity's larger influence on the formula, the lighter one takes longer to stop, even though its mass is half that of the heavier object.

Compare your answer with the correct one above

Question

A bullet with a mass of is flying through the air at a velocity of $450 \frac{m}{s}$ . What is its kinetic energy?

Answer

The equation for kinetic energy is:

$KE=\frac{1}{2}mv^2$

Plug in known values and solve.

$KE=\frac{1}{2}(0.0058kg)\left(450\frac{m}{s}\right)^2$

$KE\approx 587J$

Compare your answer with the correct one above

Question

$g=9.81 \frac{m}{s^2}$

A dumbell with a mass of has been dropped from a height of . What is the amount of kinetic energy in the dumbell after three seconds?

Answer

Since the stone starts at rest (it has an initial velocity of zero), its velocity at any time is given as:

At a time of three seconds, the velocity towards the ground is thus:

$v(3)=9.81\frac{m}{s^2}(3s)=29.43\frac{m}{s}$

It's kinetic energy at three seconds is therefore:

$KE=\frac{1}{2}mv^2$

$KE=\frac{1}{2}20kg(29.43\frac{m}{s})^2$

Compare your answer with the correct one above

Question

$g=9.81\frac{m}{s^2}$

Toby throws a baseball straight down from the top of a ridge at a speed of $30:\uptext{m/s}$ .

What will the ball's kinetic energy be after one second?

Answer

This problem can be approached in multiple ways; two will be shown here:

One method is to focus solely on the kinematics and related equations; since there is an initial velocity of $30\frac{m}{s}$ , the velocity at any time (provided the ball hasn't hit the ground) is given by the function:

$v(t)=30\frac{m}{s}+9.81\frac{m}{s^2}t$

$v(1s)=30\frac{m}{s}+9.81\frac{m}{s^2}(1s)$

$v(1s)=39.81\frac{m}{s}$

With this, the kinetic energy can be found:

$KE=\frac{1}{2}mv^2$

$KE=\frac{1}{2}(.15kg)(39.81\frac{m}{s})^2$

Another although longer method is to use an energy balance:

Wherein due to conservation of energy, the total energy of state 1 is equivalent to the total energy of state 2.

$PE_1=0.15kg(9.81\frac{m}{s^2})(100m)$

$KE_1=\frac{1}{2}(0.15kg)(30\frac{m}{s})^2$

Now to find of the ball, determine its height at a time of one second using the kinematic equation for position:

$h(t)=h_0-v_0t-\frac{1}{2}gt^2$

$h(t)=100m-30\frac{m}{s}t-\frac{1}{2}9.81\frac{m}{s^2}t^2$

$h(1s)=100m-30\frac{m}{s}(1s)-\frac{1}{2}9.81\frac{m}{s^2}(1s)^2$

$PE_2=(0.15kg)(9.81\frac{m}{s^2})(65.095m)$

Therefore:

Which confirms the answer we used with the earlier method.

Compare your answer with the correct one above

Question

An object travelling at $5: \frac{m}{s}$ has how much kinetic energy?

Answer

In this question, we are provided with the mass of an object as well as its velocity, and we are being asked to determine its kinetic energy. To do so, we'll need to use the following equation:

$K=\frac{1}{2}mv^{2}$

Plugging in the values given, we obtain:

$K=\frac{1}{2}(8: kg)(5: \frac{m}{s})^{2}=100:J$

Compare your answer with the correct one above

Question

In an investigation into energy, a student compresses a spring a distance of from its neutral length. She then puts a cart against the end of the spring and releases both the spring and the cart. She measures the kinetic energy of the cart after the spring has returned to its neutral length and finds it to be . She then repeats the experiment, but this time compresses the spring a distance of before releasing the spring and the cart. What would the cart's kinetic energy be in the second experiment?

Answer

The potential energy stored in a spring is given by

$U_S=\frac{1}{2}kx^2$

So the energy increases with the square of the compression. When the potential energy is converted to kinetic energy of the cart, it increases by a factor of .

Compare your answer with the correct one above

Question

In an investigation into energy, a student compresses a spring a distance of from its neutral length. She then puts a cart against the end of the spring and releases both the spring and the cart. She measures the velocity of the cart after the spring has returned to its neutral length and finds it to be . She then repeats the experiment, but this time compresses the spring a distance of before releasing the spring and the cart. What would the cart's velocity be in the second experiment?

Answer

The potential energy stored in a spring is given by

$U_S=\frac{1}{2}kx^2$

So doubling the compression increases the potential energy by a factor of . However, the kinetic energy:

$K=\frac{1}{2}mv^2$ , increases with the square of the velocity, so the velocity only needs to double to increase the cart's kinetic energy by a factor of .

Compare your answer with the correct one above

Question

In an investigation into energy, a student compresses a spring a distance of from its neutral length. She then puts a cart of mass against the end of the spring and releases both the spring and the cart. She measures the velocity of the cart after the spring has returned to its neutral length and finds it to be . She then repeats the experiment, but this time using a cart whose mass is before releasing the spring and the cart. What would the cart's velocity be in the second experiment?

Answer

Kinetic energy is given by:

$K=\frac{1}{2}mv^2$ , so the energy is linearly dependent on the mass, but increases with the square of the velocity. So although the mass has doubled, the velocity only needs to decrease by a factor of $\sqrt2$ to maintain the same kinetic energy. In algebraic form:

$\frac{1}{2}(2m)v^2=\frac{1}{2}mv_0^2$

Simplify.

$v^2=\frac{1}{2}v_0^2$

$v=\frac{v_0}{\sqrt2}$

Compare your answer with the correct one above

Question

In an investigation into energy, a student compresses a spring a distance of from its neutral length. She then puts a cart of mass against the end of the spring and releases both the spring and the cart. She measures the kinetic energy of the cart after the spring has returned to its neutral length and finds it to be . She then repeats the experiment, but this time using a cart whose mass is before releasing the spring and the cart. What would the cart's kinetic energy be in the second experiment?

Answer

All of the potential energy stored in the spring is converted to kinetic energy of the cart in both experiments. Although the cart's velocity will be less in the second experiment, its kinetic energy will be the same.

Compare your answer with the correct one above

Question

A soccer ball of mass 0.5kg is kicked and accelerated uniformly from rest to travel 20 meters over 3 seconds into the goal. What is the final kinetic energy of the soccer ball?

Answer

We need to know the final speed of the ball since we have all but this quantity in our formula for kinetic energy,

$KE=.5mv_{f}^2$

To find the final velocity we first find the acceleration:

$\Delta x=V_{0}t+.5at^2$

$a=4.444\frac{m}{s^2}$

$V_{f}=at=4.444\frac{m}{s^2}3=13.333\frac{m}{s}$

$KE=(0.5)(0.5kg)(13.333\frac{m}{s})^2=44.44J$

Compare your answer with the correct one above

Question

A champagne cork with a mass of 10 grams accelerates off the top of the champagne bottle at $4\frac{m}{s^2}$ for 2 seconds. What is the final kinetic energy of the cork after 2 seconds?

Answer

We can find the final velocity by multiplying the acceleration by the time. We then plug this into the formula for kinetic energy and solve. Do not forget to convert grams to kilograms.

$V=V_{0}+at$

The initial velocity of the cork was zero.

$V=(4\frac{m}{s^2})(2s)=8\frac{m}{s}$

$KE=.5mv^2=(.5)(.01kg)(8\frac{m}{s}^2)=0.32J$

Compare your answer with the correct one above

Question

Determine the kinetic energy of a mole of oxygen gas(atomic mass unit = 16Da) if each travels at speed of $v=30 \frac{m}{s}$

Answer

First, let's remember what it means to have mole of an atom given its atomic mass unit in Daltons. mole of oxygen with atomic mass of is going to be grams. In kilograms, this would be:

$16 g\frac{1kg}{1000g}=.016kg$

Plugging this into the equation for kinetic energy $E_{kinetic}$

$E_{kinetic}=\frac{1}{2}mv^2$ , where is the mass, is its velocity.

For this problem, and $v= 30\frac{m}{s}$

Therefore,

$E_{kinetic}=\frac{1}{2}.016kg*\left(30 \frac{m}{s}\right)^2= 7.2J$

Compare your answer with the correct one above

Question

There is a truck and a car on a highway going the same speed in the same direction. The car has mass while the truck has mass .

What is the correct statement about the two vehicle's kinetic energies?

Answer

The equation for kinetic energy is:

$K=\frac{1}{2}mv^{2}$

Where is the mass of an object and is the velocity of the object.

We see from the equation that mass has a linear relationship with kinetic energy and the problem statement gives that the vehicles have the same velocity. Because the car has half the mass of the truck and the same speed, the car has half as much kinetic energy as the truck.

Without specific numbers given, we can always substitute easy numbers into the equation to help understand the concept. If we say the velocity in both cases is $v=1\frac{m}{s}$ , and the car's mass is then we have:

$\frac{1}{2}(1kg)(1\frac{m}{s})^{2}=\frac{1}{2}J$

We know the truck's mass is double the car's, which yields:

$\frac{1}{2}(2kg)(1\frac{m}{s})^{2}=1J$

This makes it clear that the car has half the kinetic energy of the truck.

Compare your answer with the correct one above

Question

A block with a mass of is dropped from a height and just before it hits the ground, it has a velocity of $5 \frac{m}{s}$ . From what height was the block dropped from?

Answer

Just before impact, the block has maximum kinetic energy. Once the kinetic energy is determined, we can find the potential energy and therefore the height of the drop. We can use the following formula to determine the kinetic energy:

$KE = \frac{1}{2}mv^2$

$KE = \frac{1}{2}(10kg)(25\frac{m}{s})^2=125J$

All of this energy was previously potential energy from which we can determine the height, .

$125J = (10kg)(10\frac{m}{s^2})(h)$

Compare your answer with the correct one above

Question

Moment of inertia of hollow sphere: $I=\frac{2mr^2}{3}$

A kickball of mass and radius is on top of a hill of height , at the edge of a straight incline to the bottom. Suppose the ball was just barely pushed over the edge. Calculate the ball's velocity at the bottom of the hill. It may be assumed that the ball is essentially hollow. Ignore any losses due to friction, as well as any velocity from the initial push.

Answer

There will be two types on kinetic energy, rotational and translational.

Using conservation of energy:

$E_{initial}=E_{final}$

$KE_{initial}+PE_{initial}=KE_{final}+PE_{final}$

Initially, kinetic energy will be zero, and in the final state, potential energy will be zero.

$mgh=.5mv^2+.5I\omega^2$

Recall:

$I=\frac{2mr^2}{3}$

and

$\omega=\frac{v}{r}$

Combine equations:

$mgh=.5mv^2+.5\frac{2mr^2}{3}(\frac{v}{r})^2$

Solve for

$v=\sqrt{\frac{6}{5}gh}$

Plug in values:

$v=\sqrt{\frac{6}{5}9.8*15}$

$v=13.3\frac{m}{s}$

Compare your answer with the correct one above

Tap the card to reveal the answer