Fundamentals of Displacement, Velocity, and Acceleration - AP Physics 1
Card 0 of 20
A box is placed on a 30o frictionless incline. What is the acceleration of the box as it slides down the incline?
A box is placed on a 30o frictionless incline. What is the acceleration of the box as it slides down the incline?
To find the acceleration of the box traveling down the incline, the mass is not needed. Using the incline of the plane as the x-direction, we can see that there is no movement in the y-direction; therefore, we can use Newton's second, F = ma, in the x-direction.
There is only one force in the x-direction (gravity), however gravity is not just equal to “mg” in this case. Since the box is on an incline, the gravitational force will be equal to mgsin(30o). Substituting force into F =ma we find that mgsin(30o) = ma. We can now cancel out masses and solve for acceleration.




To find the acceleration of the box traveling down the incline, the mass is not needed. Using the incline of the plane as the x-direction, we can see that there is no movement in the y-direction; therefore, we can use Newton's second, F = ma, in the x-direction.
There is only one force in the x-direction (gravity), however gravity is not just equal to “mg” in this case. Since the box is on an incline, the gravitational force will be equal to mgsin(30o). Substituting force into F =ma we find that mgsin(30o) = ma. We can now cancel out masses and solve for acceleration.
Compare your answer with the correct one above
A submarine launches a missile from underwater. The missile passes through the surface of the sea at a velocity of  . At this point, a thruster ignites, causing the missile to accelerate in a straight line at
. At this point, a thruster ignites, causing the missile to accelerate in a straight line at  . After 10 seconds of acceleration, how far has the missile traveled?
. After 10 seconds of acceleration, how far has the missile traveled?
A submarine launches a missile from underwater. The missile passes through the surface of the sea at a velocity of 

We need our kinematic equation that relates displacement, initial velocity, and acceleration:

We can neglect gravity in this problem since the statement says that the missile accelerates in a straight line at a constant rate.
Plugging in our values, we get:


We need our kinematic equation that relates displacement, initial velocity, and acceleration:
We can neglect gravity in this problem since the statement says that the missile accelerates in a straight line at a constant rate.
Plugging in our values, we get:
Compare your answer with the correct one above
A cannon is packed with gunpowder and a ball of mass 10kg. The cannon is angled at 30 degrees. When fired, the gunpowder releases 500J of energy, which is all transferred to the cannon ball. Neglecting air resistance and friction within the cannon, how far does the ball travel before hitting the ground?
Assume 
A cannon is packed with gunpowder and a ball of mass 10kg. The cannon is angled at 30 degrees. When fired, the gunpowder releases 500J of energy, which is all transferred to the cannon ball. Neglecting air resistance and friction within the cannon, how far does the ball travel before hitting the ground?
Assume
There are two ways to solve this problem. The first and much easier way is to use the range equation. The second is using your kinematics equations.
Method 1: Range Equation
The range equation is the following:

We know everything ecvept for the initial velocity. However, we can calculate it knowing that the cannon transfers 500 J of energy to the ball. Therefore:

Rearranging for velocity:

Now we can plug everything into the range equation:

Method 2: Kinematics Equations
As in the first method, we can calculate the initial velocity of the ball:

Rearranging for velocity:

We can then split this into it's components:


We can use the y-component to calculate how long the ball is in the air. We can do one of two things:
- Calculate how long the ball takes to reach it's peak and then multiply by 2
- Calculate how lon gthe ball takes to get a velocity of -5
We'll go with method 2:

Rearranging for t:


Then we can multiply this time by the horizontal velocity (which stays constant because we are neglecting air resistance).

There are two ways to solve this problem. The first and much easier way is to use the range equation. The second is using your kinematics equations.
Method 1: Range Equation
The range equation is the following:
We know everything ecvept for the initial velocity. However, we can calculate it knowing that the cannon transfers 500 J of energy to the ball. Therefore:
Rearranging for velocity:
Now we can plug everything into the range equation:
Method 2: Kinematics Equations
As in the first method, we can calculate the initial velocity of the ball:
Rearranging for velocity:
We can then split this into it's components:
We can use the y-component to calculate how long the ball is in the air. We can do one of two things:
- Calculate how long the ball takes to reach it's peak and then multiply by 2
- Calculate how lon gthe ball takes to get a velocity of -5
We'll go with method 2:
Rearranging for t:
Then we can multiply this time by the horizontal velocity (which stays constant because we are neglecting air resistance).
Compare your answer with the correct one above
A passenger jet is beginning its decent to its final destination. If it is at a height of 3,000m and traveling at a rate of  , what should be its angle of decent to arrive in 10 minutes?
, what should be its angle of decent to arrive in 10 minutes?
A passenger jet is beginning its decent to its final destination. If it is at a height of 3,000m and traveling at a rate of 
We know that the plane needs to drop 3,000 meters in 10 minutes. Therefore, we can calculate the vertical velocity that the plane needs to be traveling at:

Knowing the plane's velocity, we can caluclate what angle at which it needs to decend to achieve this vertical velocity:

Rearranging for theta:

Plugging in our values:

We know that the plane needs to drop 3,000 meters in 10 minutes. Therefore, we can calculate the vertical velocity that the plane needs to be traveling at:
Knowing the plane's velocity, we can caluclate what angle at which it needs to decend to achieve this vertical velocity:
Rearranging for theta:
Plugging in our values:
Compare your answer with the correct one above
Upon ignition, a bottle rocket accelerates at a rate of  for
for  before it loses thrust. What is the bottle rocket's maxmimum height?
before it loses thrust. What is the bottle rocket's maxmimum height?
Neglect air resistance and assume 
Upon ignition, a bottle rocket accelerates at a rate of 

Neglect air resistance and assume
We can use our kinematics equations to determine the height of the rocket the moment it loses thrust:


If we clarify the initial state being the moment the rocket loses thrust and the final state being the point of its maximum height, we can use the expression for conservation of energy to calculate the final height:

Removing final kinetic energy (which will be zero) and substituting in our expressions for each variable:

Cancel out mass and rearrange for final height:

From the problem statement, we can determine the initial velocity:

Now that we have values for all of our variables, we can solve:

We can use our kinematics equations to determine the height of the rocket the moment it loses thrust:
If we clarify the initial state being the moment the rocket loses thrust and the final state being the point of its maximum height, we can use the expression for conservation of energy to calculate the final height:
Removing final kinetic energy (which will be zero) and substituting in our expressions for each variable:
Cancel out mass and rearrange for final height:
From the problem statement, we can determine the initial velocity:
Now that we have values for all of our variables, we can solve:
Compare your answer with the correct one above
Consider the following system:
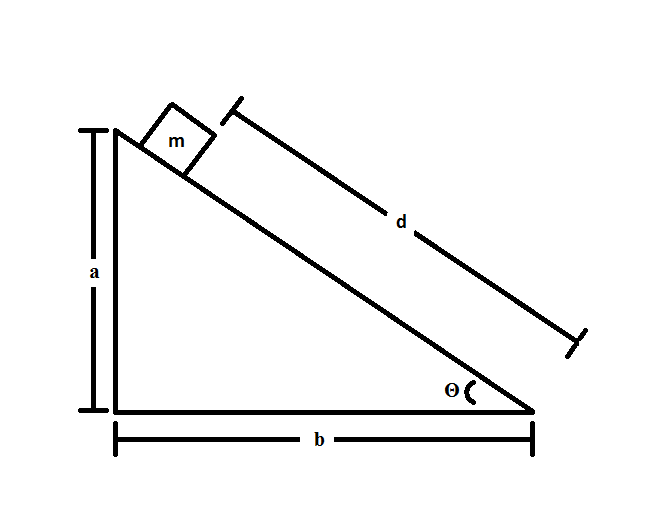
If  and
and  , what is the acceleration of the block?
, what is the acceleration of the block?

Consider the following system:

If 

There are two forces in play in this scenario: friction and gravity. We can use Newton's second law to develop an expression for the acceleration of the block:


Substituting in expressions for each force, we get:

Canceling out mass and rearranging for acceleration, we get:

We know all of our values, allowing us to solve for the acceleration:


There are two forces in play in this scenario: friction and gravity. We can use Newton's second law to develop an expression for the acceleration of the block:
Substituting in expressions for each force, we get:
Canceling out mass and rearranging for acceleration, we get:
We know all of our values, allowing us to solve for the acceleration:
Compare your answer with the correct one above
A young boy is aiming a slingshot straight upward. If the sling shot applies  of work to a ball with mass
of work to a ball with mass  , how high does the ball travel?
, how high does the ball travel?

A young boy is aiming a slingshot straight upward. If the sling shot applies 

We can use the equation for conservation of energy to solve this problem:

If we assume the initial state is when the slingshot is fully loaded and the final state is at the ball's maxmium height, we can completely eliminate kinetic energy to get:

Substituting in our value for initital potential energy and an expression for final potential energy, we get:

Rearranging for final height we get:

We can use the equation for conservation of energy to solve this problem:
If we assume the initial state is when the slingshot is fully loaded and the final state is at the ball's maxmium height, we can completely eliminate kinetic energy to get:
Substituting in our value for initital potential energy and an expression for final potential energy, we get:
Rearranging for final height we get:
Compare your answer with the correct one above
An object is moving to the right and is speeding up. Which of the following is false?
An object is moving to the right and is speeding up. Which of the following is false?
If an object is moving to the right, then its displacement is positive. If its displacement is positive then its velocity must be positive as well. The object is speeding up. This implies that the magnitude of its velocity is increasing. If this is true we have that the velocity of the object,  , after some time,
, after some time,  , has passed must be a larger positive velocity than say,
, has passed must be a larger positive velocity than say,  , the object's velocity before that time passed. Therefore, the object's average acceleration is given by:
, the object's velocity before that time passed. Therefore, the object's average acceleration is given by:
 since
since 
So we have that the object's acceleration is positive. If the object's acceleration is positive, then there must be a positive net force causing the acceleration, due to Newton's first law:  . Therefore, it is false that the object experiences a net force of 0N.
. Therefore, it is false that the object experiences a net force of 0N.
If an object is moving to the right, then its displacement is positive. If its displacement is positive then its velocity must be positive as well. The object is speeding up. This implies that the magnitude of its velocity is increasing. If this is true we have that the velocity of the object, 



So we have that the object's acceleration is positive. If the object's acceleration is positive, then there must be a positive net force causing the acceleration, due to Newton's first law: 
Compare your answer with the correct one above
An object slides across the floor moving to the left. After some time it comes to a stop. Which of the following is false?
An object slides across the floor moving to the left. After some time it comes to a stop. Which of the following is false?
If the object is moving to the left, then its displacement must be negative since its final position will be further to the left in than its initial position. So in an imaginary number line, after some time passes, the object's final position is less than the object's initial position. This can be shown mathematically:
 , since
, since 
Since the object's displacement is negative, then so is its velocity. This can easily be seen from the equation for average velocity:
 since
since  . At the end of its trajectory, the object stops, so overall the object's velocity is less than or equal to
. At the end of its trajectory, the object stops, so overall the object's velocity is less than or equal to  .
.
The object eventually stops. This means that the magnitude of the object's velocity is decreasing. In other words, the absolute value of the object's velocity is becoming smaller and smaller until it stops. So, for example, if at some moment the object's velocity is  , after some time its velocity will be
, after some time its velocity will be  . Remember that the negative sign indicates only the direction of the vector (the object is moving to the left, hence its velocity is negative). But in absolute terms, the object is moving slower and slower (to the left) until it stops. Finally, we can see that the acceleration must be positive in order to slow down an object moving to the left. Going of our example, let's say the object is moving at
. Remember that the negative sign indicates only the direction of the vector (the object is moving to the left, hence its velocity is negative). But in absolute terms, the object is moving slower and slower (to the left) until it stops. Finally, we can see that the acceleration must be positive in order to slow down an object moving to the left. Going of our example, let's say the object is moving at  and after some time it slows down to
and after some time it slows down to  (again the negative sign just indicates that the object moves to the left). So, if look at the average acceleration we have:
(again the negative sign just indicates that the object moves to the left). So, if look at the average acceleration we have:

Thus the acceleration must be positive.
If the object is moving to the left, then its displacement must be negative since its final position will be further to the left in than its initial position. So in an imaginary number line, after some time passes, the object's final position is less than the object's initial position. This can be shown mathematically:

Since the object's displacement is negative, then so is its velocity. This can easily be seen from the equation for average velocity:



The object eventually stops. This means that the magnitude of the object's velocity is decreasing. In other words, the absolute value of the object's velocity is becoming smaller and smaller until it stops. So, for example, if at some moment the object's velocity is 



Thus the acceleration must be positive.
Compare your answer with the correct one above
Which of the following statements is false regarding the relationship between an object's velocity and acceleration?
Which of the following statements is false regarding the relationship between an object's velocity and acceleration?
By definition, acceleration is the rate of change of velocity with respect to time. The average acceleration of an object is given by:

Therefore, if velocity is constant it must be the case that acceleration is 0, since the initial and final velocities of the object are equal. Similarly, if acceleration is non-zero, then it must be the case that the initial and final velocities of the object are different (so velocity is changing). Now, when an object's acceleration and initial-velocity have the same sign (i.e. the same direction) then the object will speed up. In other words, the absolute value of its velocity (the magnitude) increases. This is easy to see if we solve for the final velocity in our equation:

If both  and
and  have the same sign, then the absolute value of
have the same sign, then the absolute value of  will be greater as time passes, meaning the object is speeding up. (Try plugging in some numbers). Similarly, when
will be greater as time passes, meaning the object is speeding up. (Try plugging in some numbers). Similarly, when  and
and  have opposite signs, the magnitude of the object's velocity must start to decrease. After enough time it might even come to a stop, and if it continues to experience the acceleration it will change direction and start gaining velocity on the opposite direction. Regardless, it must first slow down (think about when you throw an object on the air).
have opposite signs, the magnitude of the object's velocity must start to decrease. After enough time it might even come to a stop, and if it continues to experience the acceleration it will change direction and start gaining velocity on the opposite direction. Regardless, it must first slow down (think about when you throw an object on the air).
Example: 

Example: 

Remember that the positive and negative signs indicate the direction of the vectors. So when it comes to slowing down or speeding up, we want to look at the magnitude of the velocity. Therefore, the only statement that is false is the one that says that if an object has both negative initial velocity and acceleration it will slow down. The object will speed up and continue to move to the left.
By definition, acceleration is the rate of change of velocity with respect to time. The average acceleration of an object is given by:
Therefore, if velocity is constant it must be the case that acceleration is 0, since the initial and final velocities of the object are equal. Similarly, if acceleration is non-zero, then it must be the case that the initial and final velocities of the object are different (so velocity is changing). Now, when an object's acceleration and initial-velocity have the same sign (i.e. the same direction) then the object will speed up. In other words, the absolute value of its velocity (the magnitude) increases. This is easy to see if we solve for the final velocity in our equation:
If both 




Example:
Example:
Remember that the positive and negative signs indicate the direction of the vectors. So when it comes to slowing down or speeding up, we want to look at the magnitude of the velocity. Therefore, the only statement that is false is the one that says that if an object has both negative initial velocity and acceleration it will slow down. The object will speed up and continue to move to the left.
Compare your answer with the correct one above
Consider three distance vs. time plots. The first displays a horizontal line at  , the second is linear with a positive slope, and the third increases quadratically. In which graph(s) do the net force acting upon it/them equal 0?
, the second is linear with a positive slope, and the third increases quadratically. In which graph(s) do the net force acting upon it/them equal 0?
Consider three distance vs. time plots. The first displays a horizontal line at 
The slope of a distance vs. time plot represents the object's velocity. Therefore, in both the first and second graphs, the velocity is constant and zero, respectively. An object with constant (or no) velocity is experiencing, by definition, no net force. Oppositely, in the third graph the slope is increasing, meaning the object is accelerating, meaning it must be subject to some force.
The slope of a distance vs. time plot represents the object's velocity. Therefore, in both the first and second graphs, the velocity is constant and zero, respectively. An object with constant (or no) velocity is experiencing, by definition, no net force. Oppositely, in the third graph the slope is increasing, meaning the object is accelerating, meaning it must be subject to some force.
Compare your answer with the correct one above

Consider the Atwood Machine above. If the mass of the sphere ( ) is
) is  and the mass of the cube (
and the mass of the cube ( ) is
) is  , when the cube is let to fall, what would the system's acceleration be?
, when the cube is let to fall, what would the system's acceleration be?

Consider the Atwood Machine above. If the mass of the sphere (



The net force experienced by m1 can be characterized as:
 where T is the tension force along the string and mg is gravity.
where T is the tension force along the string and mg is gravity.
because  is also equivalent to
is also equivalent to 
 , we can express this equation as
, we can express this equation as
 .
.
The net force experienced by m2 can similarly be expressed as:
 and
and  so
so 
From this point the problem is a system of equations.
If we solve for T in the first equation, we end up with  .
.
Then we can plug into the second equation like so:

then:

finally we can isolate a:

when we plug in the masses given by the problem, we get:

The net force experienced by m1 can be characterized as:

because 



The net force experienced by m2 can similarly be expressed as:


From this point the problem is a system of equations.
If we solve for T in the first equation, we end up with 
Then we can plug into the second equation like so:
then:
finally we can isolate a:
when we plug in the masses given by the problem, we get:
Compare your answer with the correct one above
A sports car can accelerate from  to
to  in 2s. How far does the sports car travel during the 2s of acceleration?
in 2s. How far does the sports car travel during the 2s of acceleration?
A sports car can accelerate from 

The basic kinematics equation for motion under constant acceleration is:

We do not have the acceleration, but we can find it:


Apply this to the first equation and solve.

The basic kinematics equation for motion under constant acceleration is:
We do not have the acceleration, but we can find it:
Apply this to the first equation and solve.
Compare your answer with the correct one above
A walker is walking at a constant rate of  on a circular track that is 400m in length. A runner is also on the track going in the same direction as the walker, running at an unknown constant speed. The runner and the walker are together, then meet each other again when the walker has completed
on a circular track that is 400m in length. A runner is also on the track going in the same direction as the walker, running at an unknown constant speed. The runner and the walker are together, then meet each other again when the walker has completed  of a lap, or 200m. What is the runner's speed?
of a lap, or 200m. What is the runner's speed?
A walker is walking at a constant rate of 

The equation for speed is:

The runner has gone around the track 1.5 times, thus his total distance traveled is:

We can find the elapsed time from the walker: Rearrange the speed equation to find time:

Now we have all the information we need to find the runner's speed:

The equation for speed is:
The runner has gone around the track 1.5 times, thus his total distance traveled is:
We can find the elapsed time from the walker: Rearrange the speed equation to find time:
Now we have all the information we need to find the runner's speed:
Compare your answer with the correct one above
A police officer sees a car in a  zone approaching a stop sign. The driver doesn't see the sign until the last minute and then slams on his breaks, decelerating at a constant rate to a stop just before the sign, but leaves a skid mark
zone approaching a stop sign. The driver doesn't see the sign until the last minute and then slams on his breaks, decelerating at a constant rate to a stop just before the sign, but leaves a skid mark  long. Reviewing the dash-cam tape, the officer is able to tell that the car took
long. Reviewing the dash-cam tape, the officer is able to tell that the car took  to stop. Was the driver speeding? Assume the wheels locked when the brakes were applied.
to stop. Was the driver speeding? Assume the wheels locked when the brakes were applied.
A police officer sees a car in a 


To find how fast the driver was going before applying the brakes, we use the following kinematics formula since acceleration is constant:

Where  is the displacement,
is the displacement,  is the initial velocity (before applying the brakes),
is the initial velocity (before applying the brakes),  is the final velocity (which is zero since the car came to a stop), and
is the final velocity (which is zero since the car came to a stop), and  is time. We can now plug in the known values into the above equation and solve for the initial velocity:
is time. We can now plug in the known values into the above equation and solve for the initial velocity:


In order to know if the driver was speeding, we must convert this speed and/or the speed limit in the same units. Let's put this speed in kilometers per hour.

As we can see, the driver was exceeding the  speed limit and was thus speeding.
speed limit and was thus speeding.
To find how fast the driver was going before applying the brakes, we use the following kinematics formula since acceleration is constant:
Where 



In order to know if the driver was speeding, we must convert this speed and/or the speed limit in the same units. Let's put this speed in kilometers per hour.
As we can see, the driver was exceeding the 
Compare your answer with the correct one above
Imagine a decending elevator that is increasing it's speed. What is the direction of the acceleration of the elevator?
Imagine a decending elevator that is increasing it's speed. What is the direction of the acceleration of the elevator?
A trick that I often use is if something is speeding up, the acceleration and velocity point in the same direction. If something is slowing down. the acceleration and velocity point opposite directions. Since the elevator is speeding up, the acceleration must point in the same direction as it's velocity: downwards.
A trick that I often use is if something is speeding up, the acceleration and velocity point in the same direction. If something is slowing down. the acceleration and velocity point opposite directions. Since the elevator is speeding up, the acceleration must point in the same direction as it's velocity: downwards.
Compare your answer with the correct one above
A ball is thrown straight up in the air. The ball falls back and is caught at the same location it is thrown from. At what locations does the position(y) equal zero, the velocity(v) equal zero, or the acceleration(a) equal zero? Assume the origin of my single coordinate system is placed at the location the ball is thrown.
A ball is thrown straight up in the air. The ball falls back and is caught at the same location it is thrown from. At what locations does the position(y) equal zero, the velocity(v) equal zero, or the acceleration(a) equal zero? Assume the origin of my single coordinate system is placed at the location the ball is thrown.
The origin is placed at the location the ball is thrown and caught so y=0 when it is thrown and caught. Because the ball only moves in one dimension (up or down), the velocity must drop to zero when it transitions from a upward positive velocity to a downward negative velocity at the apex. The acceleration on the surface of earth is always g for projectiles when neglecting air resistance or other forces.
The origin is placed at the location the ball is thrown and caught so y=0 when it is thrown and caught. Because the ball only moves in one dimension (up or down), the velocity must drop to zero when it transitions from a upward positive velocity to a downward negative velocity at the apex. The acceleration on the surface of earth is always g for projectiles when neglecting air resistance or other forces.
Compare your answer with the correct one above
(A)

(B)

(C)

(D)

Beverly rides her bike to the store to buy a few things. She gets her items and while riding home gets a flat tire and has to walk her bike the rest of the way. Which position vs. time graph most correctly describes the scenario? Assume her movement in the store is minimal and will be represented as no change in distance over the time she is shopping.
(A)
(B)
(C)
(D)
Beverly rides her bike to the store to buy a few things. She gets her items and while riding home gets a flat tire and has to walk her bike the rest of the way. Which position vs. time graph most correctly describes the scenario? Assume her movement in the store is minimal and will be represented as no change in distance over the time she is shopping.
Let's interpret each graph.
(A) is not correct because it shows Beverly riding her bike, being in the store for a period of time, and riding back at the same speed she was going when she rode to the store. Then she goes backward in time (not possible) and ends up at the same time and location she started at.
(B) She rides her bike to the store, stays there for a length of time and rides back. At  (arbitrary place) she has a flat time and walks home. Notice that the slopes of the position vs. time sections before and after the store are similar. The only difference is that one is positive and one is negative, indicating a positive and negative velocity respectively. Remember that a change in position over a change in time is velocity. Now she walks home which means she is traveling slower than on her bike. This means that the slope of
(arbitrary place) she has a flat time and walks home. Notice that the slopes of the position vs. time sections before and after the store are similar. The only difference is that one is positive and one is negative, indicating a positive and negative velocity respectively. Remember that a change in position over a change in time is velocity. Now she walks home which means she is traveling slower than on her bike. This means that the slope of  vs.
vs.  is smaller. It will take her a longer time to walk back so this portion has a smaller slope. She ends up at the same
is smaller. It will take her a longer time to walk back so this portion has a smaller slope. She ends up at the same  position she started from but at a later time.
position she started from but at a later time.
(C) This plot is correct if we were looking at her velocity vs. time. She starts out with a higher speed (positive) and then it's close to zero at the store. She then has a negative velocity that has the same magnitude as her trip to the store until she gets a flat and then her velocity is smaller but still negative as she walks home.
(D) This graph would be correct if she did not have a flat and rode home the entire way.
Let's interpret each graph.
(A) is not correct because it shows Beverly riding her bike, being in the store for a period of time, and riding back at the same speed she was going when she rode to the store. Then she goes backward in time (not possible) and ends up at the same time and location she started at.
(B) She rides her bike to the store, stays there for a length of time and rides back. At 



(C) This plot is correct if we were looking at her velocity vs. time. She starts out with a higher speed (positive) and then it's close to zero at the store. She then has a negative velocity that has the same magnitude as her trip to the store until she gets a flat and then her velocity is smaller but still negative as she walks home.
(D) This graph would be correct if she did not have a flat and rode home the entire way.
Compare your answer with the correct one above
Calculate the magnitude of the sum of the following two position vectors (units of  ):
):


Calculate the magnitude of the sum of the following two position vectors (units of 
The sum of two vectors written in component form will result in a new vector whose components are the sum of the components of the added vectors, written as:

The magnitude of a vector is given as the square root of the sum of the squares. Written completely as:

For our example, the solution is written in full as:

The sum of two vectors written in component form will result in a new vector whose components are the sum of the components of the added vectors, written as:
The magnitude of a vector is given as the square root of the sum of the squares. Written completely as:
For our example, the solution is written in full as:
Compare your answer with the correct one above
Given vector  has a magnitude of
has a magnitude of  directed
directed  above the
above the  axis, and vector
axis, and vector  has a magnitude of
has a magnitude of  directed
directed  above the
above the  axis, calculate
axis, calculate  .
.
Given vector 








By definition, the dot product of two vectors can be related to their magnitudes and the angle between them as follows:

Given the angle between the two vectors is  , we can calculate the dot product to be written explicitly as:
, we can calculate the dot product to be written explicitly as:

Note that the unts are  since the dot product involves multiplying two meters together.
since the dot product involves multiplying two meters together.
By definition, the dot product of two vectors can be related to their magnitudes and the angle between them as follows:
Given the angle between the two vectors is 
Note that the unts are 
Compare your answer with the correct one above