Electrostatics - AP Physics 1
Card 0 of 20
An excess charge of  is put on an ideal neutral conducting sphere with radius
is put on an ideal neutral conducting sphere with radius  . What is the Coulomb force this excess charge exerts on a point charge of
. What is the Coulomb force this excess charge exerts on a point charge of  that is
that is  from the surface of the sphere?
from the surface of the sphere?

An excess charge of 



Two principal realizations help with solving this problem, both derived from Gauss’ law for electricity:
-
The excess charge on an ideal conducting sphere is uniformly distributed over its surface
-
A uniform shell of charge acts, in terms of electric force, as if all the charge were contained in a point charge at the sphere’s center
With these realizations, an application of Coulomb’s law answers the question. If  is the point charge outside the sphere, then the force
is the point charge outside the sphere, then the force  on
on 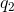 is:
is:

In this equation,  is Coulomb’s constant,
is Coulomb’s constant,  is the excess charge on the spherical conductor, and
is the excess charge on the spherical conductor, and  is total distance in meters of
is total distance in meters of  from the center of the conducting sphere.
from the center of the conducting sphere.

Using the given values in this equation, we can calculate the generated force:


Two principal realizations help with solving this problem, both derived from Gauss’ law for electricity:
-
The excess charge on an ideal conducting sphere is uniformly distributed over its surface
-
A uniform shell of charge acts, in terms of electric force, as if all the charge were contained in a point charge at the sphere’s center
With these realizations, an application of Coulomb’s law answers the question. If 

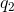
In this equation, 



Using the given values in this equation, we can calculate the generated force:
Compare your answer with the correct one above
Charges A and B are placed a distance of  from one another. The charge of particle A is
from one another. The charge of particle A is  whereas the charge of particle B is
whereas the charge of particle B is  . Charge B experiences an electrostatic force of
. Charge B experiences an electrostatic force of  from charge A. Similarly, charge A experiences an electrostatic force of
from charge A. Similarly, charge A experiences an electrostatic force of  from charge B.
from charge B.
What is the ratio of  to
to  ?
?
Charges A and B are placed a distance of 




What is the ratio of 

This question is very simple if you realize that the force experienced by both charges is equal.
The definition of the two electrostatic forces are given by Coulomb's law:

In this question, we can rewrite this equation in terms of our given system.


It doesn’t matter if the charges of the two particles are different; both particles experience the same force because the charges of both particles are accounted for in the electrostatic force equation (Coulomb's law). This conclusion can also be made by considering Newton's third law: the force of the first particle on the second will be equal and opposite the force of the second particle on the first.
Since the forces are equal, their ratio will be  .
.
This question is very simple if you realize that the force experienced by both charges is equal.
The definition of the two electrostatic forces are given by Coulomb's law:
In this question, we can rewrite this equation in terms of our given system.
It doesn’t matter if the charges of the two particles are different; both particles experience the same force because the charges of both particles are accounted for in the electrostatic force equation (Coulomb's law). This conclusion can also be made by considering Newton's third law: the force of the first particle on the second will be equal and opposite the force of the second particle on the first.
Since the forces are equal, their ratio will be 
Compare your answer with the correct one above
If the distance between two charged particles is doubled, the strength of the electric force between them will __________.
If the distance between two charged particles is doubled, the strength of the electric force between them will __________.
Coulomb's law gives the relationship between the force of an electric field and the distance between two charges:

The strength of the force will be inversely proportional to the square of the distance between the charges.
When the distance between the charges is doubled, the total force will be divided by four (quartered).

Coulomb's law gives the relationship between the force of an electric field and the distance between two charges:
The strength of the force will be inversely proportional to the square of the distance between the charges.
When the distance between the charges is doubled, the total force will be divided by four (quartered).
Compare your answer with the correct one above
Two protons are on either side of an electron as shown below:

The electron is 30 µm away from the proton on its left and 10 µm away from the proton on its right. What is the magnitude and direction of the net electric force acting on the electron?

A proton has a charge of 
Two protons are on either side of an electron as shown below:

The electron is 30 µm away from the proton on its left and 10 µm away from the proton on its right. What is the magnitude and direction of the net electric force acting on the electron?
A proton has a charge of
The net force on the electron is the sum of the forces between the electron and each of the protons:

These forces are given by Coulomb's law:

Using the numbers given, we get:


Because opposite charges attract,  points left (the negative direction) and
points left (the negative direction) and  points right (the positive direction).
points right (the positive direction).
Therefore, the net force is

Because this value is positive, the direction is rightward.
The net force on the electron is the sum of the forces between the electron and each of the protons:
These forces are given by Coulomb's law:
Using the numbers given, we get:
Because opposite charges attract, 

Therefore, the net force is
Because this value is positive, the direction is rightward.
Compare your answer with the correct one above
If we have 2 charges,  and
and  , that are
, that are  apart, what is the magnitude of the force exerted on
apart, what is the magnitude of the force exerted on  by
by  if we know that
if we know that  has a charge of
has a charge of  and
and  has a charge of
has a charge of  ?
?
If we have 2 charges, 








Use Coulomb's Law

Plug in known values and solve.


A negative value for electric force indicates an attractive force. This makes sense since our two charges have opposite signs. Since we're asked for magnitude, all answer choices are positive.
Use Coulomb's Law
Plug in known values and solve.
A negative value for electric force indicates an attractive force. This makes sense since our two charges have opposite signs. Since we're asked for magnitude, all answer choices are positive.
Compare your answer with the correct one above
If we have 2 charges,  and
and  , that are
, that are  apart, what is the force exerted on
apart, what is the force exerted on  by
by  if we know that
if we know that  has a charge of
has a charge of  and
and  has a charge of
has a charge of  ?
?
If we have 2 charges, 








Use Coulomb's law.

Plug in known values and solve.


Note that the force between two charges of the same sign (both positive or both negative) is positive. This indicates the force is repulsive, which makes sense since both charges are positive.
Use Coulomb's law.
Plug in known values and solve.
Note that the force between two charges of the same sign (both positive or both negative) is positive. This indicates the force is repulsive, which makes sense since both charges are positive.
Compare your answer with the correct one above
If we have 2 charges,  and
and  , that are
, that are  apart, what is the force exerted on
apart, what is the force exerted on  by
by  if we know that
if we know that  has a charge of
has a charge of  and
and  has a charge of
has a charge of  ?
?
If we have 2 charges, 








Use Coulomb's law.

Plug in known values and solve.


Note that this force is positive, which means it's repulsive.
Use Coulomb's law.
Plug in known values and solve.
Note that this force is positive, which means it's repulsive.
Compare your answer with the correct one above
If we have 2 charges,  and
and  , that are
, that are  apart, what is the force exerted on
apart, what is the force exerted on  by
by  if we know that
if we know that  has a charge of
has a charge of  and
and  has a charge of
has a charge of  ?
?
If we have 2 charges, 








Use Coulomb's law.

Plug in known values and solve.


Note that this force is positive, which means that it's repulsive.
Use Coulomb's law.
Plug in known values and solve.
Note that this force is positive, which means that it's repulsive.
Compare your answer with the correct one above
Two point charges,  and
and  are separated by a distance of
are separated by a distance of  . What is the force of repulsion between them?
. What is the force of repulsion between them?

Two point charges, 


The force of attraction/repulsion between two point charges is given by Coulomb's Law:

If the charges are of like sign, then there well be a repulsive force between the two. Alternatively, if the net force is positive, it is repulsive; if it is negative, it is attractive.
Therefore, the force of repulsion between the two charges is:




The force of attraction/repulsion between two point charges is given by Coulomb's Law:
If the charges are of like sign, then there well be a repulsive force between the two. Alternatively, if the net force is positive, it is repulsive; if it is negative, it is attractive.
Therefore, the force of repulsion between the two charges is:
Compare your answer with the correct one above
Two point charges,  and
and  are separated by a distance of
are separated by a distance of  . What is the work required to move them closer together to a distance of
. What is the work required to move them closer together to a distance of  ?
?

Two point charges, 



The force of attraction/repulsion between two point charges is given by Coulomb's Law:

If the charges are of like sign, then there well be a repulsive force between the two.
Work is given as the dot product of force and distance. However, in this case, force is also dependent on distance.
The amount of work required to move a charge an incremental distance,  , is given as:
, is given as:

The negative sign in this case is to account for repulsion.
The total work to change distances between charges can then be found by taking the integral with respect to distance:

Since  are constants, they can be factored out of the integral:
are constants, they can be factored out of the integral:




The force of attraction/repulsion between two point charges is given by Coulomb's Law:
If the charges are of like sign, then there well be a repulsive force between the two.
Work is given as the dot product of force and distance. However, in this case, force is also dependent on distance.
The amount of work required to move a charge an incremental distance, 
The negative sign in this case is to account for repulsion.
The total work to change distances between charges can then be found by taking the integral with respect to distance:
Since 
Compare your answer with the correct one above
Write, in vector notation, the force exerted on a positive charge of  by a negative charge of
by a negative charge of  , if the two charges sitting on the
, if the two charges sitting on the  -axis, with the positive charge sitting
-axis, with the positive charge sitting  to the right of the negative charge?
to the right of the negative charge?
Write, in vector notation, the force exerted on a positive charge of 



Coulomb's law in vector notation is given as:
 , where
, where  is Coulomb's constant,
is Coulomb's constant,  and
and  are the two charges,
are the two charges,  is the distance between the charges squared, and
is the distance between the charges squared, and  is the unit vector going from one charge to another.
is the unit vector going from one charge to another.
To write this in vector notation, we have to know the unit vector going from the negative to the positive charge, since we're trying to determine the force on the positive charge. Since they are both sitting on the  -axis, with the negative charge to the left of the positive, the unit vector will be going in the direction of positive
-axis, with the negative charge to the left of the positive, the unit vector will be going in the direction of positive  :
:

We know that 
We know that  ,
,  , and
, and  . Putting this together:
. Putting this together:


We can rewrite this as:

Coulomb's law in vector notation is given as:






To write this in vector notation, we have to know the unit vector going from the negative to the positive charge, since we're trying to determine the force on the positive charge. Since they are both sitting on the 

We know that
We know that 


We can rewrite this as:
Compare your answer with the correct one above
What are the unit(s) of Coulomb's constant  ?
?
What are the unit(s) of Coulomb's constant 
To determine this, we have to solve for  in Coulomb's law and then determine its constants.
in Coulomb's law and then determine its constants.
Recall that the magnitude of the electrostatic force between point charges is given as:
 ,
,  is the force given in
is the force given in  ,
,  and
and  are the charges given in
are the charges given in  and
and  is distance given in
is distance given in 
Solving for  ,
,

Writing out the terms on the left in their units:

Therefore,  is given in
is given in 
To determine this, we have to solve for 
Recall that the magnitude of the electrostatic force between point charges is given as:







Solving for 
Writing out the terms on the left in their units:
Therefore, 
Compare your answer with the correct one above
Two protons are at a distance  away from each other. There is a force
away from each other. There is a force  acting on each proton due to the other. If the protons are moved so that they are now at a distance
acting on each proton due to the other. If the protons are moved so that they are now at a distance
 apart, what is the new force acting on each proton due to the other
apart, what is the new force acting on each proton due to the other  ?
?
Two protons are at a distance 



Coulomb's law shows that the force between two charged particles is inversely proportional to the square of the distance between the particles.

If the distance between the charges is reduced by  , that means the
, that means the  is squared in the denominator and the
is squared in the denominator and the  will flip up to the top to give
will flip up to the top to give  time the original force. More explicitly, if we plug in the given information the initial force will be:
time the original force. More explicitly, if we plug in the given information the initial force will be:




Coulomb's law shows that the force between two charged particles is inversely proportional to the square of the distance between the particles.
If the distance between the charges is reduced by 



Compare your answer with the correct one above
Determine the strength of a force of proton on another proton in the nucleus if they are  apart.
apart.


Determine the strength of a force of proton on another proton in the nucleus if they are 
Use Coulomb's law:
 , where
, where  is Coulomb's constant,
is Coulomb's constant,  are charges of the two points and
are charges of the two points and  is the distance between the charges.
is the distance between the charges.

Use Coulomb's law:




Compare your answer with the correct one above
Two point charges, each having a charge of +1C, are 2 meters apart. If the distance between them is doubled, by what factor does the force between them change?

Two point charges, each having a charge of +1C, are 2 meters apart. If the distance between them is doubled, by what factor does the force between them change?
This is a question where knowing how to effectively sift through a problem statement and choose only the information you need will really help. We are given a bunch of values, but only need to know one thing, which is that the distance between the two charges is doubled.
Coulomb's law is as follows:

We can rewrite this for the initial and final scenarios:


We can divide one equation by the other to set up a ratio:

We know that the final radius is double the intial, which is written as:

Substituting this in we get:

Rerranging for the final force, we get:

This is a question where knowing how to effectively sift through a problem statement and choose only the information you need will really help. We are given a bunch of values, but only need to know one thing, which is that the distance between the two charges is doubled.
Coulomb's law is as follows:
We can rewrite this for the initial and final scenarios:
We can divide one equation by the other to set up a ratio:
We know that the final radius is double the intial, which is written as:
Substituting this in we get:
Rerranging for the final force, we get:
Compare your answer with the correct one above

If  ,
,  , and
, and  , then what is the magnitude of the net force on charge 2?
, then what is the magnitude of the net force on charge 2?

If 


First lets set up two axes. Have  be to the right of charge 3 and 2 in the diagram and
be to the right of charge 3 and 2 in the diagram and  be above charges 1 and 2 in the diagram with charge 2 at the origin.
be above charges 1 and 2 in the diagram with charge 2 at the origin.
Coloumb's law tells us the force between point charges is

The net force on charge 2 can be determined by combining the force on charge 2 due to charge 1 and the force on charge 2 due to charge 3.
Since charge 1 and charge 2 are of opposite polarities, they have an attractive force; therefore, charge 2 experiences a force towards charge 1 (in the  direction). By using Coloumb's law, we can determine this force to be
direction). By using Coloumb's law, we can determine this force to be

 in the
in the  direction
direction
Since charge 2 and 3 have the same polarities, they have a repulsive force; therefore, charge 2 experiences a force away from charge 2 (in the  direction). By using Coloumb's law, we can determine this force to be:
direction). By using Coloumb's law, we can determine this force to be:

 in the
in the  -direction
-direction
If we draw out these two forces tip to tail, we can construct the net force:

From this, we can see that  and
and  create a right triangle with the net force on charge 2 as the hypotenuse. By using the Pythagorean theorem, we can calculate the magnitude of the net force:
create a right triangle with the net force on charge 2 as the hypotenuse. By using the Pythagorean theorem, we can calculate the magnitude of the net force:

First lets set up two axes. Have 

Coloumb's law tells us the force between point charges is
The net force on charge 2 can be determined by combining the force on charge 2 due to charge 1 and the force on charge 2 due to charge 3.
Since charge 1 and charge 2 are of opposite polarities, they have an attractive force; therefore, charge 2 experiences a force towards charge 1 (in the 


Since charge 2 and 3 have the same polarities, they have a repulsive force; therefore, charge 2 experiences a force away from charge 2 (in the 


If we draw out these two forces tip to tail, we can construct the net force:
From this, we can see that 

Compare your answer with the correct one above
What is the force exerted on a point charge of  by a point charge of
by a point charge of  that is located
that is located  away?
away?
What is the force exerted on a point charge of 


Use Coulomb's law.

Plug in known values and solve.


Note that a positive value for electric force corresponds to a repulsive force. This should make sense since the charge on both particles are the same sign (positive).
Use Coulomb's law.
Plug in known values and solve.
Note that a positive value for electric force corresponds to a repulsive force. This should make sense since the charge on both particles are the same sign (positive).
Compare your answer with the correct one above
If we have 2 charges,  and
and  , that are
, that are  apart, what is the force exerted on
apart, what is the force exerted on  by
by  if we know that
if we know that  has a charge of
has a charge of  and
and  has a charge of
has a charge of  ?
?
If we have 2 charges, 








Use Coulomb's law.



Note that the electric force between two charges of the same sign (both positive or both negative) is a positive value. This indicates a repulsive force.
Use Coulomb's law.
Note that the electric force between two charges of the same sign (both positive or both negative) is a positive value. This indicates a repulsive force.
Compare your answer with the correct one above
A point charge of magnitude  is located 0.01m away from a point charge of magnitude
is located 0.01m away from a point charge of magnitude  . What is the electric force between the point charges?
. What is the electric force between the point charges?

A point charge of magnitude 

Use Coulomb's law to find the electric force between the charges:



Use Coulomb's law to find the electric force between the charges:
Compare your answer with the correct one above
A point charge of magnitude  is 2nm away from a point charge of identical charge. What is the electric force between the point charges?
is 2nm away from a point charge of identical charge. What is the electric force between the point charges?

A point charge of magnitude 
The electric force between two point charges is given by Coulomb's law:

Now, plug in the given charges (both the same magnitude), the given constant, and the distance between the charges (in meters) to get our answer:

The electric force between two point charges is given by Coulomb's law:
Now, plug in the given charges (both the same magnitude), the given constant, and the distance between the charges (in meters) to get our answer:
Compare your answer with the correct one above