Riemann Sum: Right Evaluation - AP Calculus BC
Card 0 of 20
Given a function  , find the Right Riemann Sum of the function on the interval
, find the Right Riemann Sum of the function on the interval ![[0,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/463614/gif.latex) divided into four sub-intervals.
divided into four sub-intervals.
Given a function 
![[0,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/463614/gif.latex)
In order to find the Riemann Sum of a given function, we need to approximate the area under the line or curve resulting from the function using rectangles spaced along equal sub-intervals of a given interval. Since we have an interval ![[0,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/463616/gif.latex) divided into
divided into  sub-intervals, we'll be using rectangles with vertices at
sub-intervals, we'll be using rectangles with vertices at  .
.
To approximate the area under the curve, we need to find the areas of each rectangle in the sub-intervals. We already know the width or base of each rectangle is  because the rectangles are spaced
because the rectangles are spaced  unit apart. Since we're looking for the Right Riemann Sum of
unit apart. Since we're looking for the Right Riemann Sum of  , we want to find the heights
, we want to find the heights 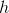 of each rectangle by taking the values of each rightmost function value on each sub-interval, as follows:
of each rectangle by taking the values of each rightmost function value on each sub-interval, as follows:




Putting it all together, the Right Riemann Sum is
 .
.
In order to find the Riemann Sum of a given function, we need to approximate the area under the line or curve resulting from the function using rectangles spaced along equal sub-intervals of a given interval. Since we have an interval ![[0,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/463616/gif.latex)


To approximate the area under the curve, we need to find the areas of each rectangle in the sub-intervals. We already know the width or base of each rectangle is 


of each rectangle by taking the values of each rightmost function value on each sub-interval, as follows:
Putting it all together, the Right Riemann Sum is

Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Given a function  , find the Right Riemann Sum of the function on the interval
, find the Right Riemann Sum of the function on the interval ![[0,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/463614/gif.latex) divided into four sub-intervals.
divided into four sub-intervals.
Given a function 
![[0,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/463614/gif.latex)
In order to find the Riemann Sum of a given function, we need to approximate the area under the line or curve resulting from the function using rectangles spaced along equal sub-intervals of a given interval. Since we have an interval ![[0,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/463616/gif.latex) divided into
divided into  sub-intervals, we'll be using rectangles with vertices at
sub-intervals, we'll be using rectangles with vertices at  .
.
To approximate the area under the curve, we need to find the areas of each rectangle in the sub-intervals. We already know the width or base of each rectangle is  because the rectangles are spaced
because the rectangles are spaced  unit apart. Since we're looking for the Right Riemann Sum of
unit apart. Since we're looking for the Right Riemann Sum of  , we want to find the heights
, we want to find the heights 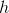 of each rectangle by taking the values of each rightmost function value on each sub-interval, as follows:
of each rectangle by taking the values of each rightmost function value on each sub-interval, as follows:




Putting it all together, the Right Riemann Sum is
 .
.
In order to find the Riemann Sum of a given function, we need to approximate the area under the line or curve resulting from the function using rectangles spaced along equal sub-intervals of a given interval. Since we have an interval ![[0,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/463616/gif.latex)


To approximate the area under the curve, we need to find the areas of each rectangle in the sub-intervals. We already know the width or base of each rectangle is 


of each rectangle by taking the values of each rightmost function value on each sub-interval, as follows:
Putting it all together, the Right Riemann Sum is

Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{1}^{15.8}(-15sin(14e^{(4x)}))dx\&\text{So the interval is }[1,15.8]\text{ the subintervals have length }\frac{15.8-(1)}{4}=\frac{37}{10}\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[\frac{47}{10},\frac{42}{5},\frac{121}{10},\frac{79}{5}]\&\int_{1}^{15.8}(-15sin(14e^{(4x)}))dx=\frac{37}{10}[(-15sin(14e^{(4(\frac{47}{10}))}))+(-15sin(14e^{(4(\frac{42}{5}))}))+(-15sin(14e^{(4(\frac{121}{10}))}))+(-15sin(14e^{(4(\frac{79}{5}))}))]\&\int_{1}^{15.8}(-15sin(14e^{(4x)}))dx=20.79\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935039/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{4}^{14}(-8sin(12e^{(x)}))dx\&\text{So the interval is }[4,14]\text{ the subintervals have length }\frac{14-(4)}{4}=\frac{5}{2}\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[\frac{13}{2},9,\frac{23}{2},14]\&\int_{4}^{14}(-8sin(12e^{(x)}))dx=\frac{5}{2}[(-8sin(12e^{((\frac{13}{2}))}))+(-8sin(12e^{((9))}))+(-8sin(12e^{((\frac{23}{2}))}))+(-8sin(12e^{((14))}))]\&\int_{4}^{14}(-8sin(12e^{(x)}))dx=-17.23\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935088/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{0}^{6}(5x - 1000sin(3x)^{2})dx\&\text{So the interval is }[0,6]\text{ the subintervals have length }\frac{6-(0)}{4}=\frac{3}{2}\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[\frac{3}{2},3,\frac{9}{2},6]\&\int_{0}^{6}(5x - 1000sin(3x)^{2})dx=\frac{3}{2}[(5(\frac{3}{2}) - 1000sin(3(\frac{3}{2}))^{2})+(5(3) - 1000sin(3(3))^{2})+(5(\frac{9}{2}) - 1000sin(3(\frac{9}{2}))^{2})+(5(6) - 1000sin(3(6))^{2})]\&\int_{0}^{6}(5x - 1000sin(3x)^{2})dx=-3390.69\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935090/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{-4}^{-1.6}(15cos(12sin(6x)) + 5x^{3})dx\&\text{So the interval is }[-4,-1.6]\text{ the subintervals have length }\frac{-1.6-(-4)}{3}=\frac{4}{5}\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935046/gif.latex)
![\begin{align*}\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[-\frac{16}{5},-\frac{12}{5},-\frac{8}{5}]\&\int_{-4}^{-1.6}(15cos(12sin(6x)) + 5x^{3})dx\approx\frac{4}{5}[(15cos(12sin(6(-\frac{16}{5}))) + 5(-\frac{16}{5})^{3})+(15cos(12sin(6(-\frac{12}{5}))) + 5(-\frac{12}{5})^{3})+(15cos(12sin(6(-\frac{8}{5}))) + 5(-\frac{8}{5})^{3})]\&\int_{-4}^{-1.6}(15cos(12sin(6x)) + 5x^{3})dx\approx-208.73\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935047/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{0}^{13.6}(2x + 4sin(3tan(5x)))dx\&\text{So the interval is }[0,13.6]\text{ the subintervals have length }\frac{13.6-(0)}{4}=\frac{17}{5}\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935242/gif.latex)
![\begin{align*}\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[\frac{17}{5},\frac{34}{5},\frac{51}{5},\frac{68}{5}]\&\int_{0}^{13.6}(2x + 4sin(3tan(5x)))dx\approx\frac{17}{5}[(2(\frac{17}{5}) + 4sin(3tan(5(\frac{17}{5}))))+(2(\frac{34}{5}) + 4sin(3tan(5(\frac{34}{5}))))+(2(\frac{51}{5}) + 4sin(3tan(5(\frac{51}{5}))))+(2(\frac{68}{5}) + 4sin(3tan(5(\frac{68}{5}))))]\&\int_{0}^{13.6}(2x + 4sin(3tan(5x)))dx\approx214.27\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935243/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{-4}^{7.1}(4x - 15sin(13x^{2}))dx\&\text{So the interval is }[-4,7.1]\text{ the subintervals have length }\frac{7.1-(-4)}{3}=\frac{37}{10}\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[-\frac{3}{10},\frac{17}{5},\frac{71}{10}]\&\int_{-4}^{7.1}(4x - 15sin(13x^{2}))dx\approx\frac{37}{10}[(4(-\frac{3}{10}) - 15sin(13(-\frac{3}{10})^{2}))+(4(\frac{17}{5}) - 15sin(13(\frac{17}{5})^{2}))+(4(\frac{71}{10}) - 15sin(13(\frac{71}{10})^{2}))]\&\int_{-4}^{7.1}(4x - 15sin(13x^{2}))dx\approx74.37\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935282/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{-1}^{15}(3x + 5sin(2e^{(2x)}))dx\&\text{So the interval is }[-1,15]\text{ the subintervals have length }\frac{15-(-1)}{4}=4\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[3,7,11,15]\&\int_{-1}^{15}(3x + 5sin(2e^{(2x)}))dx\approx4[(3(3) + 5sin(2e^{(2(3))}))+(3(7) + 5sin(2e^{(2(7))}))+(3(11) + 5sin(2e^{(2(11))}))+(3(15) + 5sin(2e^{(2(15))}))]\&\int_{-1}^{15}(3x + 5sin(2e^{(2x)}))dx\approx431.64\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935322/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{3}^{4.8}(4x + 16cos(13e^{(3x)}))dx\&\text{So the interval is }[3,4.8]\text{ the subintervals have length }\frac{4.8-(3)}{3}=\frac{3}{5}\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[\frac{18}{5},\frac{21}{5},\frac{24}{5}]\&\int_{3}^{4.8}(4x + 16cos(13e^{(3x)}))dx\approx\frac{3}{5}[(4(\frac{18}{5}) + 16cos(13e^{(3(\frac{18}{5}))}))+(4(\frac{21}{5}) + 16cos(13e^{(3(\frac{21}{5}))}))+(4(\frac{24}{5}) + 16cos(13e^{(3(\frac{24}{5}))}))]\&\int_{3}^{4.8}(4x + 16cos(13e^{(3x)}))dx\approx34.93\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935287/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{-5}^{15}(4x + 18sin(tan(5x)))dx\&\text{So the interval is }[-5,15]\text{ the subintervals have length }\frac{15-(-5)}{4}=5\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[0,5,10,15]\&\int_{-5}^{15}(4x + 18sin(tan(5x)))dx\approx5[(4(0) + 18sin(tan(5(0))))+(4(5) + 18sin(tan(5(5))))+(4(10) + 18sin(tan(5(10))))+(4(15) + 18sin(tan(5(15))))]\&\int_{-5}^{15}(4x + 18sin(tan(5x)))dx\approx527.09\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935248/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{2}^{4}(2x - 10tan(8tan(3x)))dx\&\text{So the interval is }[2,4]\text{ the subintervals have length }\frac{4-(2)}{4}=\frac{1}{2}\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[\frac{5}{2},3,\frac{7}{2},4]\&\int_{2}^{4}(2x - 10tan(8tan(3x)))dx\approx\frac{1}{2}[(2(\frac{5}{2}) - 10tan(8tan(3(\frac{5}{2}))))+(2(3) - 10tan(8tan(3(3))))+(2(\frac{7}{2}) - 10tan(8tan(3(\frac{7}{2}))))+(2(4) - 10tan(8tan(3(4))))]\&\int_{2}^{4}(2x - 10tan(8tan(3x)))dx\approx11.06\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935320/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{-2}^{8.2}(3x - sin(15e^{(4x)}))dx\&\text{So the interval is }[-2,8.2]\text{ the subintervals have length }\frac{8.2-(-2)}{3}=\frac{17}{5}\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[\frac{7}{5},\frac{24}{5},\frac{41}{5}]\&\int_{-2}^{8.2}(3x - sin(15e^{(4x)}))dx\approx\frac{17}{5}[(3(\frac{7}{5}) - sin(15e^{(4(\frac{7}{5}))}))+(3(\frac{24}{5}) - sin(15e^{(4(\frac{24}{5}))}))+(3(\frac{41}{5}) - sin(15e^{(4(\frac{41}{5}))}))]\&\int_{-2}^{8.2}(3x - sin(15e^{(4x)}))dx\approx148.47\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935285/gif.latex)

![\begin{align*}&\text{A Riemann sum integral approximation over an interval [a, b]}\&\text{with n subintervals follows the form:}\&\int_a^b f(x)dx \approx \frac{b-a}{n}(f(x_1)+f(x_2)+...+f(x_n))\&\text{It is essentially a sum of n rectangles, each with a base of}\&\text{length :}\frac{b-a}{n}\text{ and variable heights :}f(x_i)\text{, which depend on the function value at }x_i\&\text{We're asked to approximate}\int_{5}^{6.5}(2x + 7\cdot 3^{(5sin(x))})dx\&\text{So the interval is }[5,6.5]\text{ the subintervals have length }\frac{6.5-(5)}{3}=\frac{1}{2}\&\text{and since we are using the *right*point of each interval, the x-values are:}\&[\frac{11}{2},6,\frac{13}{2}]\&\int_{5}^{6.5}(2x + 7\cdot 3^{(5sin(x))})dx\approx\frac{1}{2}[(2(\frac{11}{2}) + 7\cdot 3^{(5sin((\frac{11}{2})))})+(2(6) + 7\cdot 3^{(5sin((6)))})+(2(\frac{13}{2}) + 7\cdot 3^{(5sin((\frac{13}{2})))})]\&\int_{5}^{6.5}(2x + 7\cdot 3^{(5sin(x))})dx\approx30.24\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/935280/gif.latex)