Maclaurin Series for exponential and trigonometric functions - AP Calculus BC
Card 0 of 4
Find the Maclaurin Series of the function
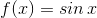
up to the fifth degree.
Find the Maclaurin Series of the function
up to the fifth degree.
The formula for an i-th degree Maclaurin Polynomial is

For the fifth degree polynomial, we must evaluate the function up to its fifth derivative.


The summation becomes

And substituting for the values of the function and the first five derivative values, we get the Maclaurin Polynomial

The formula for an i-th degree Maclaurin Polynomial is
For the fifth degree polynomial, we must evaluate the function up to its fifth derivative.
The summation becomes
And substituting for the values of the function and the first five derivative values, we get the Maclaurin Polynomial
Compare your answer with the correct one above
Write out the first three terms of the Taylor series about 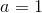 for the following function:
for the following function:

Write out the first three terms of the Taylor series about 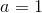
The Taylor series about x=a for a function is given by

For the first three terms (n=0, 1, 2) we must find the zeroth, first, and second derivative of the function. The zeroth derivative is just the function itself.
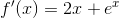

The derivatives were found using the following rules:
 ,
,

Now, using the above formula, write out the first three terms:
![\frac{(1+e^1)(x-1)^0}{0!}+\frac{[(2+e^1)(x-1)^1]}{1!}+\frac{(2+e^1)(x-1)^2}{2!}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436367/gif.latex)
which simplified becomes
![(1+e^1)+[(2+e^1)(x-1)]+\frac{(2+e^1)(x-1)^2}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436368/gif.latex)
The Taylor series about x=a for a function is given by
For the first three terms (n=0, 1, 2) we must find the zeroth, first, and second derivative of the function. The zeroth derivative is just the function itself.
The derivatives were found using the following rules:

Now, using the above formula, write out the first three terms:
which simplified becomes
Compare your answer with the correct one above
Find the Maclaurin Series of the function
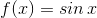
up to the fifth degree.
Find the Maclaurin Series of the function
up to the fifth degree.
The formula for an i-th degree Maclaurin Polynomial is

For the fifth degree polynomial, we must evaluate the function up to its fifth derivative.


The summation becomes

And substituting for the values of the function and the first five derivative values, we get the Maclaurin Polynomial

The formula for an i-th degree Maclaurin Polynomial is
For the fifth degree polynomial, we must evaluate the function up to its fifth derivative.
The summation becomes
And substituting for the values of the function and the first five derivative values, we get the Maclaurin Polynomial
Compare your answer with the correct one above
Write out the first three terms of the Taylor series about 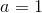 for the following function:
for the following function:

Write out the first three terms of the Taylor series about 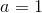
The Taylor series about x=a for a function is given by

For the first three terms (n=0, 1, 2) we must find the zeroth, first, and second derivative of the function. The zeroth derivative is just the function itself.
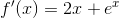

The derivatives were found using the following rules:
 ,
,

Now, using the above formula, write out the first three terms:
![\frac{(1+e^1)(x-1)^0}{0!}+\frac{[(2+e^1)(x-1)^1]}{1!}+\frac{(2+e^1)(x-1)^2}{2!}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436367/gif.latex)
which simplified becomes
![(1+e^1)+[(2+e^1)(x-1)]+\frac{(2+e^1)(x-1)^2}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/436368/gif.latex)
The Taylor series about x=a for a function is given by
For the first three terms (n=0, 1, 2) we must find the zeroth, first, and second derivative of the function. The zeroth derivative is just the function itself.
The derivatives were found using the following rules:

Now, using the above formula, write out the first three terms:
which simplified becomes
Compare your answer with the correct one above