Slope of a curve at a point - AP Calculus AB
Card 0 of 20
If 
 , what is the value of
, what is the value of  ?
?
If 

The function is not differentiable at  . So the derivative at
. So the derivative at  does not exist.
does not exist.
The function is not differentiable at 

Compare your answer with the correct one above
Find the slope of the curve  , at
, at  .
.
Find the slope of the curve 

Find the derivative of the curve using the power rule.
In mathematical terms, the power rule states,

Therefore the derivative is,

Next, plug in the x-value to find the slope of the curve at  , which gives you a final answer of
, which gives you a final answer of 
Find the derivative of the curve using the power rule.
In mathematical terms, the power rule states,
Therefore the derivative is,
Next, plug in the x-value to find the slope of the curve at 
Compare your answer with the correct one above
Find the slope of the curve,  , at
, at  .
.
Find the slope of the curve, 

Expand the binomial and combine like terms to get,

Next, take the derivative of the polynomial using the power rule, which is in mathematical terms,

Therefore,

Lastly, plug in  for
for  , to get the slope at the point.
, to get the slope at the point.
This gives you your final answer of 
Expand the binomial and combine like terms to get,
Next, take the derivative of the polynomial using the power rule, which is in mathematical terms,
Therefore,
Lastly, plug in 

This gives you your final answer of
Compare your answer with the correct one above
Find the slope of the curve  at the point with x-coordinate
at the point with x-coordinate  .
.
Find the slope of the curve 

To find the slope at a point, we take the derivative of  , substitute in
, substitute in  , and simplify.
, and simplify.
 .
.
 .
.
To find the slope at a point, we take the derivative of 



Compare your answer with the correct one above
Find k'(1) if  .
.
Find k'(1) if 
First, find the derivative. You should get  .
.
Next, plug in x=1.
You should get  .
.
First, find the derivative. You should get 
Next, plug in x=1.
You should get 
Compare your answer with the correct one above
Find the slope of  at t=0.
at t=0.
Find the slope of 
First, use the chain rule to find f'(t).
You should get  .
.
Next, plug in t=0 to get f'(0)= .
.
First, use the chain rule to find f'(t).
You should get 
Next, plug in t=0 to get f'(0)=
Compare your answer with the correct one above
Find the slope at the point (1,2) of the function

Find the slope at the point (1,2) of the function
Derivatives are slope finders. Therefore to find the slope at the given point, we need to find the derivative of the function using power rule. Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent.
So, we get 
From there we plug in our x value.


Derivatives are slope finders. Therefore to find the slope at the given point, we need to find the derivative of the function using power rule. Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent.
So, we get
From there we plug in our x value.
Compare your answer with the correct one above
Find m in  from the equation, given the point (2,0)
from the equation, given the point (2,0)

Find m in 
To find the tangent line at the given point, we need to first take the derivative of the given function.
To find the derivative we need to use product rule. Product rule states that we take the derivative of the first function and multiply it by the derivative of the second function and then add that with the derivative of the second function multiplied by the given first function. To find the derivative of each separate function we need to use power rule.

Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent



Use power rule and we get :

From here, to find the slope at the given point we plug in "2" for x.
)(-3(2%5E2))&space;+&space;(-&space;(2%5E3)+4)(2(2)+2))
This comes out to equal 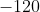
To find the tangent line at the given point, we need to first take the derivative of the given function.
To find the derivative we need to use product rule. Product rule states that we take the derivative of the first function and multiply it by the derivative of the second function and then add that with the derivative of the second function multiplied by the given first function. To find the derivative of each separate function we need to use power rule.
Power rule says that we take the exponent of the “x” value and bring it to the front. Then we subtract one from the exponent
Use power rule and we get :
From here, to find the slope at the given point we plug in "2" for x.
This comes out to equal
Compare your answer with the correct one above
Find the slope of the curve  at the point
at the point 
Find the slope of the curve 
To find the slope of the curve at any point, we take its derivative

We then evaluate ate the point  ,
,

To find the slope of the curve at any point, we take its derivative
We then evaluate ate the point 
Compare your answer with the correct one above
Find the rate of change of f(x) at the point (4,12).

Find the rate of change of f(x) at the point (4,12).
Find the rate of change of f(x) at the point (4,12)

We are asked to find a rate of change, so begin by finding the first derivative.


Now, we need the rate of change at (4,12). What matters most is the x value, simply plug it into our derivative and solve for y

So, our answer is 1271
Find the rate of change of f(x) at the point (4,12)
We are asked to find a rate of change, so begin by finding the first derivative.
Now, we need the rate of change at (4,12). What matters most is the x value, simply plug it into our derivative and solve for y
So, our answer is 1271
Compare your answer with the correct one above
Find the slope of the function  at the point
at the point 
Find the slope of the function 
To find the slope at a point of our function, we need to find its derivative first.
Using the product rule (and the chain rule within this product rule application), we have
 .
.
Plugging the  -value of our point into this equation, we get our desired slope of
-value of our point into this equation, we get our desired slope of
 .
.
To find the slope at a point of our function, we need to find its derivative first.
Using the product rule (and the chain rule within this product rule application), we have

Plugging the 

Compare your answer with the correct one above
Find the slope of the line tangent to f(x) at the point x=0.

Find the slope of the line tangent to f(x) at the point x=0.
Find the slope of the line tangent to f(x) at the point x=0

To find the slope of a tangent line, we must first find the derivative of our function.
Let's recall a few rules to help us out.
- The derivative of a monomial can be found by multiplying the coefficient by the exponent, and then decreasing the exponent by 1.

- The derivative of e to the x is e to the x

- The derivative of cosine is negative sine

Now, put it all together to get:

Lastly, we need to plug in 0 for x and solve our equation.

So, our answer is 0
Find the slope of the line tangent to f(x) at the point x=0
To find the slope of a tangent line, we must first find the derivative of our function.
Let's recall a few rules to help us out.
- The derivative of a monomial can be found by multiplying the coefficient by the exponent, and then decreasing the exponent by 1.
- The derivative of e to the x is e to the x
- The derivative of cosine is negative sine
Now, put it all together to get:
Lastly, we need to plug in 0 for x and solve our equation.
So, our answer is 0
Compare your answer with the correct one above
If  , what is the slope of the curve at the point
, what is the slope of the curve at the point  ?
?
If 

To find the slope at a point, we first find the derivative of our function, and then substitute in the  -value of our point.
-value of our point.
 , so
, so  , and plugging in our
, and plugging in our  -value gives
-value gives  .
.
To find the slope at a point, we first find the derivative of our function, and then substitute in the 




Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above
Compare your answer with the correct one above













