Functions, Graphs, and Limits - AP Calculus AB
Card 0 of 20
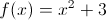 when
when  and
and
 when
when 
At  the funciton described above is:
the funciton described above is:
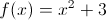


At 
The answer is both.
If graphed the student will see that the two graphs are continuous at  . There is no gap in the graph or no uneven transitions. If the graph is continuous then it is differentiable so it must be both.
. There is no gap in the graph or no uneven transitions. If the graph is continuous then it is differentiable so it must be both.
The answer is both.
If graphed the student will see that the two graphs are continuous at 
Compare your answer with the correct one above
Which of the following functions contains a removeable discontinuity?
Which of the following functions contains a removeable discontinuity?
A removeable discontinuity occurs whenever there is a hole in a graph that could be fixed (or "removed") by filling in a single point. Put another way, if there is a removeable discontinuity at  , then the limit as
, then the limit as  approaches
approaches  exists, but the value of
exists, but the value of  does not.
does not.
For example, the function  contains a removeable discontinuity at
contains a removeable discontinuity at  . Notice that we could simplify
. Notice that we could simplify as follows:
as follows:
 , where
, where  .
.
Thus, we could say that  .
.
As we can see, the limit of  exists at
exists at  , even though
, even though  is undefined.
is undefined.
What this means is that  will look just like the parabola with the equation
will look just like the parabola with the equation  EXCEPT when
EXCEPT when , where there will be a hole in the graph. However, if we were to just define
, where there will be a hole in the graph. However, if we were to just define  , then we could essentially "remove" this discontinuity. Therefore, we can say that there is a removeable discontinuty at
, then we could essentially "remove" this discontinuity. Therefore, we can say that there is a removeable discontinuty at  .
.
The functions
 , and
, and

have discontinuities, but these discontinuities occur as vertical asymptotes, not holes, and thus are not considered removeable.
The functions
 and
and  are continuous over all the real values of
are continuous over all the real values of  ; they have no discontinuities of any kind.
; they have no discontinuities of any kind.
The answer is
 .
.
A removeable discontinuity occurs whenever there is a hole in a graph that could be fixed (or "removed") by filling in a single point. Put another way, if there is a removeable discontinuity at 



For example, the function 




Thus, we could say that 
As we can see, the limit of 


What this means is that 




The functions

have discontinuities, but these discontinuities occur as vertical asymptotes, not holes, and thus are not considered removeable.
The functions



The answer is

Compare your answer with the correct one above
Is the following piecewise function continuous for all  ? If not, state where it is discontinuous.
? If not, state where it is discontinuous.

Is the following piecewise function continuous for all 
To check if the piecewise function is continuous, all we need to do is check that the values at 3 and 5 line up.
At  , this means checking that
, this means checking that  and
and  have the same value. More formally, we are checking to see that
have the same value. More formally, we are checking to see that  , as to be continuous at a point, a function's left and right limits must both equal the function value at that point.
, as to be continuous at a point, a function's left and right limits must both equal the function value at that point.
Plugging 3 into both, we see that both of them are 12 at  . Thus, they meet up smoothly.
. Thus, they meet up smoothly.
Next, for  , we have
, we have  and
and  . Plugging in 5, we get 22 for both equations.
. Plugging in 5, we get 22 for both equations.
As all three equations are polynomials, we know they will be continuous everywhere else, and they meet up smoothly at the piecewise bounds, thus ensuring that the function is continuous everywhere.
Note, there are sharp turns at  and
and  , but this only means the function isn't differentiable at these points -- we're only concerned with continuity, which is if the equations meet up. Thus, the function is continuous.
, but this only means the function isn't differentiable at these points -- we're only concerned with continuity, which is if the equations meet up. Thus, the function is continuous.
To check if the piecewise function is continuous, all we need to do is check that the values at 3 and 5 line up.
At 



Plugging 3 into both, we see that both of them are 12 at 
Next, for 


As all three equations are polynomials, we know they will be continuous everywhere else, and they meet up smoothly at the piecewise bounds, thus ensuring that the function is continuous everywhere.
Note, there are sharp turns at 

Compare your answer with the correct one above
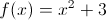 when
when  and
and
 when
when 
At  the funciton described above is:
the funciton described above is:
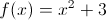


At 
The answer is both.
If graphed the student will see that the two graphs are continuous at  . There is no gap in the graph or no uneven transitions. If the graph is continuous then it is differentiable so it must be both.
. There is no gap in the graph or no uneven transitions. If the graph is continuous then it is differentiable so it must be both.
The answer is both.
If graphed the student will see that the two graphs are continuous at 
Compare your answer with the correct one above
Which of the following functions contains a removeable discontinuity?
Which of the following functions contains a removeable discontinuity?
A removeable discontinuity occurs whenever there is a hole in a graph that could be fixed (or "removed") by filling in a single point. Put another way, if there is a removeable discontinuity at  , then the limit as
, then the limit as  approaches
approaches  exists, but the value of
exists, but the value of  does not.
does not.
For example, the function  contains a removeable discontinuity at
contains a removeable discontinuity at  . Notice that we could simplify
. Notice that we could simplify as follows:
as follows:
 , where
, where  .
.
Thus, we could say that  .
.
As we can see, the limit of  exists at
exists at  , even though
, even though  is undefined.
is undefined.
What this means is that  will look just like the parabola with the equation
will look just like the parabola with the equation  EXCEPT when
EXCEPT when , where there will be a hole in the graph. However, if we were to just define
, where there will be a hole in the graph. However, if we were to just define  , then we could essentially "remove" this discontinuity. Therefore, we can say that there is a removeable discontinuty at
, then we could essentially "remove" this discontinuity. Therefore, we can say that there is a removeable discontinuty at  .
.
The functions
 , and
, and

have discontinuities, but these discontinuities occur as vertical asymptotes, not holes, and thus are not considered removeable.
The functions
 and
and  are continuous over all the real values of
are continuous over all the real values of  ; they have no discontinuities of any kind.
; they have no discontinuities of any kind.
The answer is
 .
.
A removeable discontinuity occurs whenever there is a hole in a graph that could be fixed (or "removed") by filling in a single point. Put another way, if there is a removeable discontinuity at 



For example, the function 




Thus, we could say that 
As we can see, the limit of 


What this means is that 




The functions

have discontinuities, but these discontinuities occur as vertical asymptotes, not holes, and thus are not considered removeable.
The functions



The answer is

Compare your answer with the correct one above
Is the following piecewise function continuous for all  ? If not, state where it is discontinuous.
? If not, state where it is discontinuous.

Is the following piecewise function continuous for all 
To check if the piecewise function is continuous, all we need to do is check that the values at 3 and 5 line up.
At  , this means checking that
, this means checking that  and
and  have the same value. More formally, we are checking to see that
have the same value. More formally, we are checking to see that  , as to be continuous at a point, a function's left and right limits must both equal the function value at that point.
, as to be continuous at a point, a function's left and right limits must both equal the function value at that point.
Plugging 3 into both, we see that both of them are 12 at  . Thus, they meet up smoothly.
. Thus, they meet up smoothly.
Next, for  , we have
, we have  and
and  . Plugging in 5, we get 22 for both equations.
. Plugging in 5, we get 22 for both equations.
As all three equations are polynomials, we know they will be continuous everywhere else, and they meet up smoothly at the piecewise bounds, thus ensuring that the function is continuous everywhere.
Note, there are sharp turns at  and
and  , but this only means the function isn't differentiable at these points -- we're only concerned with continuity, which is if the equations meet up. Thus, the function is continuous.
, but this only means the function isn't differentiable at these points -- we're only concerned with continuity, which is if the equations meet up. Thus, the function is continuous.
To check if the piecewise function is continuous, all we need to do is check that the values at 3 and 5 line up.
At 



Plugging 3 into both, we see that both of them are 12 at 
Next, for 


As all three equations are polynomials, we know they will be continuous everywhere else, and they meet up smoothly at the piecewise bounds, thus ensuring that the function is continuous everywhere.
Note, there are sharp turns at 

Compare your answer with the correct one above

Compare your answer with the correct one above
Find all vertical asymptotes and horizontal asymptotes of the function,

Find all vertical asymptotes and horizontal asymptotes of the function,

1) To find the horizontal asymptotes, find the limit of the function as  ,
,

Therefore, the function  has a horizontal asymptote
has a horizontal asymptote 
________________________________________________________________
2) Vertical asympototes will occur at points where the function blows up,  . For rational functions this behavior occurs when the denominator approaches zero.
. For rational functions this behavior occurs when the denominator approaches zero.
Factor the denominator and set to zero,


So the graph of  has two vertical asymptotes, one at
has two vertical asymptotes, one at  and the other at
and the other at  . They have been drawn into the graph of
. They have been drawn into the graph of  below. The blue curves represent
below. The blue curves represent  .
.

1) To find the horizontal asymptotes, find the limit of the function as 
Therefore, the function 
________________________________________________________________
2) Vertical asympototes will occur at points where the function blows up, 
Factor the denominator and set to zero,
So the graph of 




Compare your answer with the correct one above
Evaluate

Evaluate
The equation  will have a horizontal asymptote y=4.
will have a horizontal asymptote y=4.
We can find the horizontal asymptote by looking at the terms with the highest power.
The terms with the highest power here are  in the numerator and
in the numerator and  in the denominator. These terms will "take over" the function as x approaches infinity. That means the limit will reach the ratio of the two terms.
in the denominator. These terms will "take over" the function as x approaches infinity. That means the limit will reach the ratio of the two terms.
The ratio is 
The equation 
We can find the horizontal asymptote by looking at the terms with the highest power.
The terms with the highest power here are 

The ratio is
Compare your answer with the correct one above

Compare your answer with the correct one above
For this infinity limit, we need to consider the leading terms of both the numerator and the denominator. In our problem, the leading term of the numerator is larger than the leading term of the denominator. Therefore, it will be growing at a faster rate.

Now, simply input the limit value, and interpret the results.

For this infinity limit, we need to consider the leading terms of both the numerator and the denominator. In our problem, the leading term of the numerator is larger than the leading term of the denominator. Therefore, it will be growing at a faster rate.
Now, simply input the limit value, and interpret the results.
Compare your answer with the correct one above
For infinity limits, we need only consider the leading term in both the numerator and the denominator. Here, we have the case that the exponents are equal in the leading terms. Therefore, the limit at infinity is simply the ratio of the coefficients of the leading terms.

For infinity limits, we need only consider the leading term in both the numerator and the denominator. Here, we have the case that the exponents are equal in the leading terms. Therefore, the limit at infinity is simply the ratio of the coefficients of the leading terms.
Compare your answer with the correct one above
Infinity limits can be found by only considering the leading term in both the numerator and the denominator. In this problem, the numerator has a higher exponent than the denominator. Therefore, it will keep increasing and increasing at a much faster rate. These limits always tend to infinity.


Infinity limits can be found by only considering the leading term in both the numerator and the denominator. In this problem, the numerator has a higher exponent than the denominator. Therefore, it will keep increasing and increasing at a much faster rate. These limits always tend to infinity.
Compare your answer with the correct one above
For infinity limits, we only consider the leading term in both the numerator and the denominator. Then, we need to consider the exponents of the leading terms. Here, the denominator has a higher degree than the numerator. Therefore, we have a bottom heavy fraction. Even though we are evaluating the limit at negative infinity, this will still tend to zero because the denominator is growing at a faster rate. You can convince yourself of this by plugging in larger and larger negative values. You will just get a longer and smaller decimal.


For infinity limits, we only consider the leading term in both the numerator and the denominator. Then, we need to consider the exponents of the leading terms. Here, the denominator has a higher degree than the numerator. Therefore, we have a bottom heavy fraction. Even though we are evaluating the limit at negative infinity, this will still tend to zero because the denominator is growing at a faster rate. You can convince yourself of this by plugging in larger and larger negative values. You will just get a longer and smaller decimal.
Compare your answer with the correct one above

Compare your answer with the correct one above

Compare your answer with the correct one above

Compare your answer with the correct one above

Compare your answer with the correct one above

Compare your answer with the correct one above

Compare your answer with the correct one above



















