Using e - Algebra II
Card 0 of 12
On the day of a child's birth, a sum of money is to be invested into a certificate of deposit (CD) that draws  annual interest compounded continuously. The plan is for the value of the CD to be at least
annual interest compounded continuously. The plan is for the value of the CD to be at least  on the child's
on the child's  birthday.
birthday.
If the amount of money invested is to be a multiple of  , what is the minimum that should be invested initially, assuming that there are no further deposits or withdrawals?
, what is the minimum that should be invested initially, assuming that there are no further deposits or withdrawals?
On the day of a child's birth, a sum of money is to be invested into a certificate of deposit (CD) that draws 


If the amount of money invested is to be a multiple of 
If we let  be the initial amount invested and
be the initial amount invested and  be the annual interest rate of the CD expressed as a decimal, then at the end of
be the annual interest rate of the CD expressed as a decimal, then at the end of  years, the amount of money
years, the amount of money 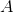 that the CD will be worth can be determined by the formula
that the CD will be worth can be determined by the formula

Substitute  ,
,  ,
, 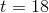 , and solve for
, and solve for  .
.

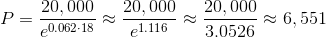
The minimum principal to be invested initially is $6,551. However, since we are looking for the multiple of $1,000 that guarantees a minimum final balance of $20,000, we round up to the nearest such multiple, which is $7,000 - the correct response.
If we let 


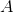
Substitute 

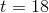

The minimum principal to be invested initially is $6,551. However, since we are looking for the multiple of $1,000 that guarantees a minimum final balance of $20,000, we round up to the nearest such multiple, which is $7,000 - the correct response.
Compare your answer with the correct one above
Twelve years ago, your grandma put money into a savings account for you that earns  interest annually and is continuously compounded. How much money is currently in your account if she initially deposited
interest annually and is continuously compounded. How much money is currently in your account if she initially deposited  and you have not taken any money out?
and you have not taken any money out?
Twelve years ago, your grandma put money into a savings account for you that earns 

1. Use  where
where  is the current amount,
is the current amount,  is the interest rate,
is the interest rate,  is the amount of time in years since the initial deposit, and
is the amount of time in years since the initial deposit, and  is the amount initially deposited.
is the amount initially deposited.



2. Solve for 



You currently have $24,596 in your account.
1. Use 




2. Solve for
You currently have $24,596 in your account.
Compare your answer with the correct one above
Solve for 

Solve for
Step 1: Achieve same bases



Step 2: Drop bases and set exponents equal to eachother

Step 3: Solve for 


Step 1: Achieve same bases
Step 2: Drop bases and set exponents equal to eachother
Step 3: Solve for
Compare your answer with the correct one above
Solve for 

Solve for
Step 1: Achieve same bases



Step 2: Drop bases and set exponents equal to eachother

Step 3: Solve for 


Step 1: Achieve same bases
Step 2: Drop bases and set exponents equal to eachother
Step 3: Solve for
Compare your answer with the correct one above
Solve for 

Solve for
Step 1: Achieve same bases



Step 2: Drop bases, set exponenets equal to eachother

Step 3: Solve for 



Step 1: Achieve same bases
Step 2: Drop bases, set exponenets equal to eachother
Step 3: Solve for
Compare your answer with the correct one above
Solve for 

Solve for
Step 1: Achieve same bases



Step 2: Drop bases, set exponents equal to eachother

Step 3: Solve for x


Step 1: Achieve same bases
Step 2: Drop bases, set exponents equal to eachother
Step 3: Solve for x
Compare your answer with the correct one above
Solve for 

Solve for
Step 1: Achieve same bases


Step 2: Drop bases, set exponents equal to eachother

Step 3: Solve for 

Step 1: Achieve same bases
Step 2: Drop bases, set exponents equal to eachother
Step 3: Solve for
Compare your answer with the correct one above
Solve: 
Solve:
To solve  , it is necessary to know the property of
, it is necessary to know the property of  .
.

Since  and the
and the  terms cancel due to inverse operations, the answer is what's left of the
terms cancel due to inverse operations, the answer is what's left of the  term.
term.
The answer is: 
To solve 

Since 


The answer is:
Compare your answer with the correct one above
Simplify: 
Simplify:
In order to eliminate the natural log on both side, we will need to raise both sides as a power with a base of  . This will cancel out the natural logs.
. This will cancel out the natural logs.

The equation will become:

Subtract  on both sides.
on both sides.

Simplify both sides.

Divide both sides by negative five.

The answer is: 
In order to eliminate the natural log on both side, we will need to raise both sides as a power with a base of 
The equation will become:
Subtract 
Simplify both sides.
Divide both sides by negative five.
The answer is:
Compare your answer with the correct one above
Simplify: 
Simplify:
In order to cancel the natural logs, we will need to use  as a base and raise both raise both sides as the quantity of the power.
as a base and raise both raise both sides as the quantity of the power.

The equation becomes: 
Subtract  and add three on both sides.
and add three on both sides.
![2x-3 -[2x]+(3)=x^2-[2x]+(3)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/840260/gif.latex)
The equation becomes: 
Use the quadratic equation to solve for the possible roots.

Simplify the quadratic equation.

The answers are: 
In order to cancel the natural logs, we will need to use 
The equation becomes:
Subtract 
The equation becomes:
Use the quadratic equation to solve for the possible roots.
Simplify the quadratic equation.
The answers are:
Compare your answer with the correct one above
Simplify: 
Simplify:
In order to get rid of the natural log, we will need to use the exponential term  as a base and raise both sides as the powers using this base.
as a base and raise both sides as the powers using this base.

The equation becomes:

Subtract nine from both sides.


Divide by three on both sides.

Simplify both sides.
The answer is: 
In order to get rid of the natural log, we will need to use the exponential term 
The equation becomes:
Subtract nine from both sides.
Divide by three on both sides.
Simplify both sides.
The answer is:
Compare your answer with the correct one above
Simplify: 
Simplify:
In order to solve for the x-variable, we will need to raise both sides as powers of base  , since the natural log has a default base of
, since the natural log has a default base of  .
.

The equation becomes:

Add three on both sides.

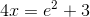
Divide by four on both sides.

The equation is: 
The answer is: 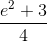
In order to solve for the x-variable, we will need to raise both sides as powers of base 

The equation becomes:
Add three on both sides.
Divide by four on both sides.
The equation is:
The answer is:
Compare your answer with the correct one above