Transformations of Parabolic Functions - Algebra II
Card 0 of 20
If the function  is depicted here, which answer choice graphs
is depicted here, which answer choice graphs  ?
?

If the function 

The function  shifts a function f(x)
shifts a function f(x)  units to the left. Conversely,
units to the left. Conversely,  shifts a function f(x)
shifts a function f(x)  units to the right. In this question, we are translating the graph two units to the left.
units to the right. In this question, we are translating the graph two units to the left.
To translate along the y-axis, we use the function  or
or  .
.
The function 



To translate along the y-axis, we use the function 

Compare your answer with the correct one above
Consider the following two functions:
 and
and 
How is the function  shifted compared with
shifted compared with  ?
?
Consider the following two functions:

How is the function 

The  portion results in the graph being shifted 3 units to the left, while the
portion results in the graph being shifted 3 units to the left, while the  results in the graph being shifted six units down. Vertical shifts are the same sign as the number outside the parentheses, while horizontal shifts are the OPPOSITE direction as the sign inside the parentheses, associated with
results in the graph being shifted six units down. Vertical shifts are the same sign as the number outside the parentheses, while horizontal shifts are the OPPOSITE direction as the sign inside the parentheses, associated with  .
.
The 


Compare your answer with the correct one above
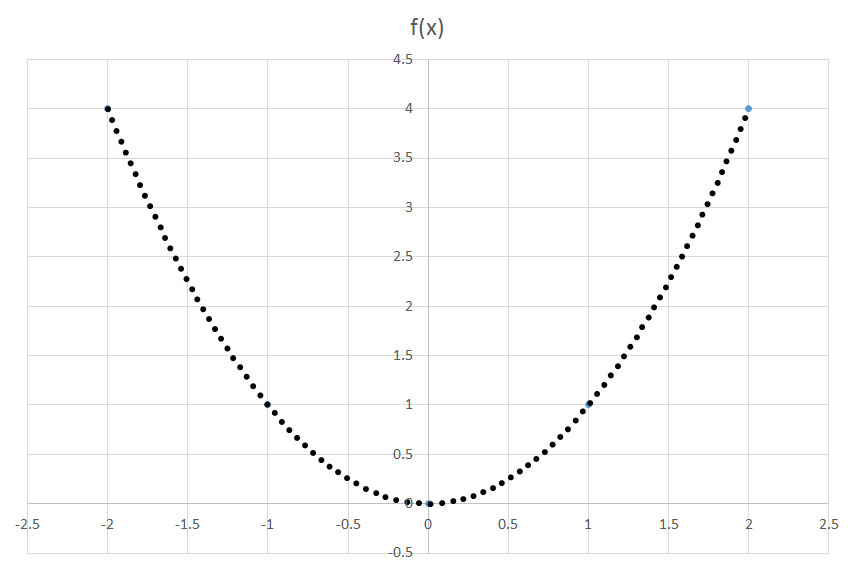
Select the function that accuratley fits the graph shown.

Select the function that accuratley fits the graph shown.
The parent function of a parabola is  where
where  are the vertex.
are the vertex.
The original graph of a parabolic (quadratic) function has a vertex at (0,0) and shifts left or right by h units and up or down by k units.
.
This function then shifts 1 unit left, and 4 units down, and the negative in front of the squared term denotes a rotation over the x-axis.

Correct Answer: 
The parent function of a parabola is 

The original graph of a parabolic (quadratic) function has a vertex at (0,0) and shifts left or right by h units and up or down by k units.
.
This function then shifts 1 unit left, and 4 units down, and the negative in front of the squared term denotes a rotation over the x-axis.
Correct Answer:
Compare your answer with the correct one above
State the vertex of the following parabola

State the vertex of the following parabola
Without doing much work or manipulation of the function, we can use our knowledge of Vertex Form of quadratic functions, which is 
with  being the coordinates of the vertex. Knowing this, we can analyze our function
being the coordinates of the vertex. Knowing this, we can analyze our function  to find the vertex...
to find the vertex... 
 vertex:
vertex:  .
.
Note: This function is simply a transformation of the function 
Without doing much work or manipulation of the function, we can use our knowledge of Vertex Form of quadratic functions, which is
with 




Note: This function is simply a transformation of the function
Compare your answer with the correct one above
Transform the following parabola:  .
.
Shift up  and to the left
and to the left  .
.
Transform the following parabola: 
Shift up 

When transforming paraboloas, to translate up, add to the equation (or add to the Y).
To translate to the left, add to the X.
Don't forget that if you add to the X, then since X is squared, the addition to X must also be squared.
 with the shift up 5 becomes:
with the shift up 5 becomes:  .
.
Now adding the shift to the left we get:
 .
.
When transforming paraboloas, to translate up, add to the equation (or add to the Y).
To translate to the left, add to the X.
Don't forget that if you add to the X, then since X is squared, the addition to X must also be squared.


Now adding the shift to the left we get:

Compare your answer with the correct one above
Transform the following parabola  .
.
Move  units to the left.
units to the left.
Move  unit down.
unit down.
Transform the following parabola 
Move 
Move 
To move unit down, subtract from Y (or from the entire equation) , so subtract 1.
To move unit to the left, add to X (don't forget, that since you are squaring X, you must square the addition as well).
With the move down our equation  becomes:
becomes:  .
.
Now to move it to the left we get  .
.
To move unit down, subtract from Y (or from the entire equation) , so subtract 1.
To move unit to the left, add to X (don't forget, that since you are squaring X, you must square the addition as well).
With the move down our equation 

Now to move it to the left we get 
Compare your answer with the correct one above

Which function represents  being shifted to the left
being shifted to the left 
 ?
?
Which function represents 


The parent function for a parabolic function is  where
where  is the center of the parabola. To shift the parabola left of right, the value of h changes. Since there is a negative sign in the parent function, a positive value moves the parabola to the left and a negative value moves it to the right.
is the center of the parabola. To shift the parabola left of right, the value of h changes. Since there is a negative sign in the parent function, a positive value moves the parabola to the left and a negative value moves it to the right.
The parent function for a parabolic function is 

Compare your answer with the correct one above
Transformations of Parabolic Functions
Given the function:

write the equation of a new function  that has been translated right 2 spaces and up 4 spaces.
that has been translated right 2 spaces and up 4 spaces.
Transformations of Parabolic Functions
Given the function:
write the equation of a new function 
Translations that effect x must be directly connected to x in the function and must also change the sign. So when the function was translated right two spaces, a  must be connected to the x value in the function.
must be connected to the x value in the function.
Translation that effect y must be directly connected to the constant in the funtion - so when the function was translated up 4 spaces a +4 must be added to the (-5) in the original function.
When both of these happen in the function the new function must become:
must become:

Translations that effect x must be directly connected to x in the function and must also change the sign. So when the function was translated right two spaces, a 
Translation that effect y must be directly connected to the constant in the funtion - so when the function was translated up 4 spaces a +4 must be added to the (-5) in the original function.
When both of these happen in the function the new function
Compare your answer with the correct one above
List the transformations of the following function:

List the transformations of the following function:
Because the parent function is  , we can write the general form as:
, we can write the general form as:
 .
.
a is the compression or stretch factor.
If  , the function compresses or "narrows" by a factor of a.
, the function compresses or "narrows" by a factor of a.
If  , the function stretches or "widens" by a factor of a.
, the function stretches or "widens" by a factor of a.
b represents how the function shifts horizontally.
If b is negative, the function shifts to the left b units.
If b is positive, the function shifts to the right b units.
c represents how the function shifts vertically.
If c is positive, the function shifts up c units.
If c is negative, the function shifts down c units.
For our problem, a=3, b=-2, and c=5. (Remember that even though b is negative, the negative from the "general form" makes the sign positive). It follows that we have a compression by a factor of 3, a horizontal shift to the left 2 units, and a vertical shift up 5 units.
Because the parent function is 

a is the compression or stretch factor.
If 
If 
b represents how the function shifts horizontally.
If b is negative, the function shifts to the left b units.
If b is positive, the function shifts to the right b units.
c represents how the function shifts vertically.
If c is positive, the function shifts up c units.
If c is negative, the function shifts down c units.
For our problem, a=3, b=-2, and c=5. (Remember that even though b is negative, the negative from the "general form" makes the sign positive). It follows that we have a compression by a factor of 3, a horizontal shift to the left 2 units, and a vertical shift up 5 units.
Compare your answer with the correct one above
Write the equation for  shifted 4 units up and 5 units to the left.
shifted 4 units up and 5 units to the left.
Write the equation for 
Right now, the vertex for this point is  , so to shift it up 4 and left 5 would place it at
, so to shift it up 4 and left 5 would place it at  .
.
This gives us an equation of  .
.
We could also get this by adding 5 inside the parentheses for the left 5 shift, and adding 4 on the outside for the up 4 shift.
Right now, the vertex for this point is 

This gives us an equation of 
We could also get this by adding 5 inside the parentheses for the left 5 shift, and adding 4 on the outside for the up 4 shift.
Compare your answer with the correct one above
Give the equation of the parabola  reflected over the
reflected over the  -axis.
-axis.
Give the equation of the parabola 

Flipping this equation over the x-axis means that the sign of y changes.
The easiest way to accomplish this is just to multiply everything by -1.

Flipping this equation over the x-axis means that the sign of y changes.
The easiest way to accomplish this is just to multiply everything by -1.
Compare your answer with the correct one above
Which would be the equation of  when reflected over the
when reflected over the  -axis?
-axis?
Which would be the equation of 

To flip this over the  -axis, the sign of x changes.
-axis, the sign of x changes.
This entails changing  to
to  .
.
 .
.
Perhaps a simpler way to think about this is that the vertex for this parabola is at  .
.
If we flip the equation over the y-axis, it will place the vertex at  , making our new equation
, making our new equation  .
.
To flip this over the 
This entails changing 


Perhaps a simpler way to think about this is that the vertex for this parabola is at 
If we flip the equation over the y-axis, it will place the vertex at 

Compare your answer with the correct one above
Write the equation for the parabola  shifted 3 units to the right and then reflected across the
shifted 3 units to the right and then reflected across the  -axis.
-axis.
Write the equation for the parabola 

To solve this problem, we could complete the square and shift the equation that way, but the vertex ends up being  so this may not be an ideal method. Instead, we know we're shifting the equation 3 units to the right, so we can just plug in
so this may not be an ideal method. Instead, we know we're shifting the equation 3 units to the right, so we can just plug in  for every appearance of x:
for every appearance of x:

To simplify, first expand 

Now we can plug that in and continue simplifying:
 distribute the 2; combine -3 and -5
distribute the 2; combine -3 and -5
 combine like terms -12x and x; 18 and -8
combine like terms -12x and x; 18 and -8

Now we want to flip this over the x-axis, meaning that the y coordinates change sign.
This means we have to multiply everything by -1, or simply change the sign of every term on the right side:

To solve this problem, we could complete the square and shift the equation that way, but the vertex ends up being 

To simplify, first expand
Now we can plug that in and continue simplifying:


Now we want to flip this over the x-axis, meaning that the y coordinates change sign.
This means we have to multiply everything by -1, or simply change the sign of every term on the right side:
Compare your answer with the correct one above
Write the equation for the parabola  after it has been reflected over the y-axis, then shifted up 2 and left 4.
after it has been reflected over the y-axis, then shifted up 2 and left 4.
Write the equation for the parabola 
First, reflect the equation over the y-axis by switching the sign of x:

Now shift up 2 by adding 2:

Now shift left 4 by adding 4 to x:
 first expand
first expand 

Now multiply 
Now plug those back in:
 combine like terms
combine like terms

First, reflect the equation over the y-axis by switching the sign of x:
Now shift up 2 by adding 2:
Now shift left 4 by adding 4 to x:

Now multiply
Now plug those back in:

Compare your answer with the correct one above
Translate the parabola  up 6 units and right 3.
up 6 units and right 3.
Translate the parabola 
To shift up 6 units, just add 6:

To shift to the right 3, subtract 3 from x:

First expand  :
:

now this gives us:
 distribute the 2 and the 4:
distribute the 2 and the 4:
 combine like terms:
combine like terms:

To shift up 6 units, just add 6:
To shift to the right 3, subtract 3 from x:
First expand 
now this gives us:


Compare your answer with the correct one above
Describe the translation in

from the parent function
 .
.
Describe the translation in
from the parent function

Below is the standard equation for parabolas;



Therefore,

 and
and 
thus,
the translation from the parent function is down three units, right one unit.
Below is the standard equation for parabolas;
Therefore,

thus,
the translation from the parent function is down three units, right one unit.
Compare your answer with the correct one above
Given the parabola  , what is the new equation if the parabola is shifted left two units, and up four units?
, what is the new equation if the parabola is shifted left two units, and up four units?
Given the parabola 
Shifting up and down will result in a change in the y-intercept.
Add four to the equation.
![y=2(x-2)^2+3+[4] =2(x-2)^2+7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/732331/gif.latex)
Shifting the parabola to the left two units will change the inner term  to
to  , which will be
, which will be  .
.
Replace the  quantity with
quantity with  .
.
The new equation is: 
Shifting up and down will result in a change in the y-intercept.
Add four to the equation.
Shifting the parabola to the left two units will change the inner term 


Replace the 

The new equation is:
Compare your answer with the correct one above
Shift  to the left two units and up two units. What is the new equation?
to the left two units and up two units. What is the new equation?
Shift 
Vertical shifts will change the value of the y-intercept. Since this function is to be shifted up two units, add two to the right side of the equation.


This graph shifted two units to the left indicates that its zeros will also shift to the left two units, which means that the  term will become
term will become  .
.
Rewrite the equation and expand the binomials.


The new equation is: 
Vertical shifts will change the value of the y-intercept. Since this function is to be shifted up two units, add two to the right side of the equation.
This graph shifted two units to the left indicates that its zeros will also shift to the left two units, which means that the 

Rewrite the equation and expand the binomials.
The new equation is:
Compare your answer with the correct one above
Compare your answer with the correct one above
Shift the parabola  three units to the right. What is the new equation?
three units to the right. What is the new equation?
Shift the parabola 
Shifting this graph three units to the right means that the x-variable will need to be replaced with  . Rewrite the equation.
. Rewrite the equation.

Use the FOIL method to simplify the binomial.

Simplify the right side.

The equation becomes:

The answer is: 
Shifting this graph three units to the right means that the x-variable will need to be replaced with 
Use the FOIL method to simplify the binomial.
Simplify the right side.
The equation becomes:
The answer is:
Compare your answer with the correct one above





