Hyperbolic Functions - Algebra II

Card 0 of 20

Question

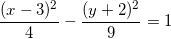
$\small \frac{(x-3)^{2}}{4}-\frac{(y+2)^{2}}{9}=1$

In which direction does the graph of the above hyperbola open?

Answer

To determine which direction a hyperbola opens, first get the equation into standard form for a conic section:

$\small \small \frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$

This equation gives us a hyperbola when the coefficient in front of either the x-squared or the y-squared term (but not both!) is negative. In this problem, the coefficient in front of the x-squared term is positive, but the coefficient of the y-squared term is negative. Here are the rules for hyperbola directions:

If the coefficient of the x-squared term is positive but the coefficient of the y-squared term is negative, this is a hyperbola that opens horizontally.

If the coefficient of the x-squared term is negative but the coefficient of the y-squared term is positive, this is a hyperbola that opens vertically.

Thus, we have a graph of a horizontal hyperbola.

Compare your answer with the correct one above

Question

What are the vertices of this hyperbola?

$\frac{(x-2)^2}{4}-(y-5)^2=1$

Answer

The first thing we need to find for this hyperbola is the center. This is simply the point where and both equal , which is . Since the term is the positive one, the hyperbola opens horizontally, which means we need to look at the denominator of that term.

The denominator is which is , so our vertices are $(2\pm 2, 5)$ , or

and .

Compare your answer with the correct one above

Question

Write the expression for this hyperbola in standard form:

${}y^2-6y-x^2+4x=-1}$

Answer

The standard form of a hyperbola is

$\large \frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1$

or the similar form with a positive term and negative term. So to start out getting this equation in standard form, we must complete the square on the quadratics in and .

the coefficient of is , so completing the square we get

${y^2-6y = (y-3)^2-9}$

and similarly with we get

${ -x^2+4x = -(x-2)^2+4}$

and so our starting expression can be written as

${(y-3)^2-(x-2)^2=-1+9-4 = 4}$

Dividing by on both sides we get the standard representation of the hyperbola,

${ \frac{(y-3)^2}{4}-\frac{(x-2)^2}{4}=1}$

Compare your answer with the correct one above

Question

Find the vertices of the following hyperbolic function:

$\frac{(x-2)^2}{16}-\frac{(y+3)^2}{9}=1$

Answer

We start by noticing that our hyperbola is given in the following form:

$\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1$

In order to determine the vertices of the hyperbola, we must first locate its center. Using the standard form given above, we know the center of the hyperbola occurs at the point (h,k), so for the equation given in the problem the center is at (2,-3). Now that we know the location of the hyperbola's center, our next step is to determine how far the vertices are from the center of the hyperbola. Looking at our equation, we can see it is in the form where the x term occurs first, which means the hyperbola opens left and right as opposed to up and down (which would be the case if the y term occurred first. Given this information, we know the vertices of the hyperbola are going to be a distance to the left and right of the center. The denominator of the x term in the hyperbolic equation is 16, which means is equal to 4, so the vertices of the hyperbola will be 4 units to the left and right of the center (2,-3), which gives us:

and

Compare your answer with the correct one above

Question

Which of the following equations represents a vertical hyperbola with a center of and asymptotes at $y=\pm, \frac{4}{3}, x$ ?

Answer

First, we need to become familiar with the standard form of a hyperbolic equation:

$\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1$

The center is always at . This means that for this problem, the numerators of each term will have to contain $(x+4)^{2}$ and $(y-3)^{2}$ .

To determine if a hyperbola opens vertically or horizontally, look at the sign of each variable. A vertical parabola has a positive $y^{2}$ term; a horizontal parabola has a positive $x^{2}$ term. In this case, we need a vertical parabola, so the $y^{2}$ term will have to be positive.

(NOTE: If both terms are the same sign, you have an ellipse, not a parabola.)

The asymptotes of a parabola are always found by the equation $y=\pm, \frac{b}{a}, x$ , where is found in the denominator of the $y^{2}$ term and is found in the denominator of the $x^{2}$ term. Since our asymptotes are $y=\pm, \frac{4}{3}, x$ , we know that must be 4 and must be 3. That means that the number underneath the $y^{2}$ term has to be 16, and the number underneath the $x^{2}$ term has to be 9.

Compare your answer with the correct one above

Question

What is the shape of the graph depicted by the equation:

$\small \frac{y^2}{9}-\frac{x^2}{4}=1$

Answer

The standard equation of a hyperbola is:

$\small \frac{y^2}{a^2}-\frac{x^2}{b^2}=1$

Compare your answer with the correct one above

Question

Express the following hyperbolic function in standard form:

Answer

In order to express the given hyperbolic function in standard form, we must write it in one of the following two ways:

$\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1$

$\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}=1$

From our formulas for the standard form of a hyperbolic equation above, we can see that the term on the right side of the equation is always 1, so we must divide both sides of the given equation by 52, which gives us:

$\frac{13(y-7)^2}{52}-\frac{13(x+6)^2}{52}=1$

Simplifying, we obtain our final answer in standard form:

$\frac{(y-7)^2}{4}-\frac{(x+6)^2}{4}=1$

Compare your answer with the correct one above

Question

Which of the following answers best represent $2\sinh(x)$ ?

Answer

The correct definition of hyperbolic sine is:

$\sinh(x)= \frac{e^x-e^-^x}{2}$

Therefore, by multiplying 2 by both sides we get the following answer,

$2\sinh(x)=e^x-e^-^x$

Compare your answer with the correct one above

Question

Which of the following best represents $\cosh(x)-\sinh(x)$ , if the value of is zero?

Answer

Find the values of hyperbolic sine and cosine when x is zero. According to the properties:

$\sinh(0)=\frac{e^x-e^{-x}}{2}=\frac{e^0-e^{-0}}{2}=\frac{1-1}{2}=0$

$\cosh(0)= \frac{e^x+e^{-x}}{2}=\frac{e^0+e^{-0}}{2}=\frac{1+1}{2}=\frac{2}{2}=1$

Therefore:

$\cosh(0)-\sinh(0)=1-0=1$

Compare your answer with the correct one above

Question

What is the value of $-\tanh(0)$ ?

Answer

The hyperbolic tangent will need to be rewritten in terms of hyperbolic sine and cosine.

According to the properties:

$\sinh(0)=0$

$\cosh(0)=1$

Therefore:

$-\tanh(0)= -\frac{\sinh(0)}{\cosh(0)}=-\frac{\frac{e^0-e^0}{2}}{\frac{e^0+e^0}{2}}=-\frac{e^0-e^0}{e^0+e^0}=-\frac{0}{1} = 0$

Compare your answer with the correct one above

Question

Simplify: $-\frac{1}{\sinh^2(x)-\cosh^2(x)}$

Answer

The following is a property of hyperbolics that is closely similar to the problem.

$\cosh^2(x) -\sinh^2(x)= 1$

We will need to rewrite this equation by taking a negative one as the common factor, and divide the negative one on both sides.

$(-1)(-\cosh^2(x) +\sinh^2(x))= 1$

$-\cosh^2(x) +\sinh^2(x)= -1$

$\sinh^2(x)-\cosh^2(x) =-1$

Substitute the value into the problem.

$-\frac{1}{sinh^2(x)-cosh^2(x)} = - \frac{1}{-1} =1$

Compare your answer with the correct one above

Question

$\small f(x)=\tfrac{1}{x+4}-3$

Which of the following is the correct expression for a hyperbola that is shifted $\small 5$ $\small units$ units up and $\small 2$ $\small units$ to the right of $\small f(x)$ ?

Answer

The parent function of a hyperbola is represented by the function $\small \small \small \small g(x)=\tfrac{1}{x-h}+k$ where $\small (h,k)$ is the center of the hyperbola. To shift the original function up by $\small 5$ $\small units$ simply add $\small -3+5$ . To shift it to the right $\small 2$ $\small units$ take away $\small 4-2$ .

Compare your answer with the correct one above

Question

Find the foci of the hyperbola: $-\frac{x^2}{36}+\frac{y^2}{16} =1$

Answer

Write the standard forms for a hyperbola.

$\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2} =1$

OR:

$-\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2} =1$

The standard form is given in the second case, which will have different parameters compared to the first form.

Center:

Foci: $(h,k\pm c)$ , where

$-\frac{x^2}{36}+\frac{y^2}{16} =1$

Identify the coefficients and substitute to find the value of .

$a^2 = 36, a=\pm6$

$b^2 =16, b=\pm 4$

$c^2 =a^2+b^2\rightarrow c^2 =36+16$

$c^2=52, c=\pm \sqrt{52} =\pm \sqrt{4}\cdot \sqrt{13}= \pm2\sqrt{13}$

$(h,k\pm c) = (0,0 \pm 2\sqrt{13}) = (0,\pm 2\sqrt{13})$

The answer is: $(0,\pm 2\sqrt{13})$

Compare your answer with the correct one above

Question

Given the hyperbola , what is the value of the center?

Answer

In order to determine the center, we will first need to rewrite this equation in standard form.

$\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}=1$

Isolate 41 on the right side. Subtract and add on both sides.

The equation becomes:

Group the x and y terms. Be careful of the negative signs.

Pull out a common factor of 4 on the second parentheses.

Complete the square twice. Divide the second term of each parentheses by two and square the quantity. Add the terms on both sides.

$(y^2+4y+(\frac{4}{2})^2)-4(x^2-6x+(\frac{-6}{3})^2)= 41+(\frac{4}{2})^2+(-4)(\frac{-6}{3})^2$

This equation becomes:

Factorize the left side and simplify the right.

Divide both sides by nine.

$\frac{(y+2)^2}{9}-\frac{4}{9}(x-3)^2 = \frac{9}{9}$

$\frac{(y+2)^2}{9}-\frac{4(x-3)^2 }{9}=1$

The equation is now in the standard form of a hyperbola.

The center is at:

The answer is:

Compare your answer with the correct one above

Question

In which direction does the graph of the hyperbola open?

Answer

The equation for a horizontal hyperbola is . The equation for a vertical hyperbola is . The x-term appears first, so the given equation represents a horizontal hyperbola.

Compare your answer with the correct one above

Question

Which of the following shapes does the graph of the equation take?

Answer

The equation for a horizontal hyperbola is . The equation for a vertical hyperbola is . Both include x- and y-terms combined using subtraction. The equation for an ellipse is . Because the given equation connects the x- and y-terms using addition rather than subtraction, it represents an ellipse rather than a hyperbola. If the equation took the form , it would represent a circle. If the equation took the form , it would represent a parabola.

Compare your answer with the correct one above

Question

Which of the following shapes does the graph of the equation take?

Answer

The equation for a horizontal hyperbola is . The equation for a vertical hyperbola is . Both include x- and y-terms combined using subtraction. If the equation took the form (using addition rather than subtraction to combine the x- and y-terms), it would represent an ellipse. If the equation took the form , it would represent a circle. If the equation took the form , it would represent a parabola.

Compare your answer with the correct one above

Question

What are the coordinates of the center of the hyperbolic inequality $\frac{[(y+2)^{2}]}{9}-\frac{[(x-1)^{2}]}{4}\geq 1$ ?

Answer

The equation for a horizontal hyperbola is $\frac{[(x-h)^{2}]}{(a^{2})}-\frac{[(y-v)^{2}]}{(b^{2})}=1$ . The equation for a vertical hyperbola is $\frac{[(y-v)^{2}]}{(b^{2})}-\frac{[(x-h)^{2}]}{(a^{2})}=1$ . In both, (h, v) is the center of the hyperbola. Hyperbolic inequalities use an inequality sign rather than an equals sign, but otherwise have the same form as hyperbolic equations. Because the two terms are combined using subtraction and the y-term appears first, this inequality represents a vertical hyperbola. To derive the center of a hyperbola from its equation or inequality, flip the sign of the constants that appear after the x and y in the equation or inequality. The constant following x is -1, so the x-coordinate of the center is 1. The constant following y is 2, so the y-coordinate of the center is -2.

The graph of the hyperbolic inequality $\frac{[(y+2)^{2}]}{9}-\frac{[(x-1)^{2}]}{4}\geq 1$ appears as follows:

With vertices of (1, 1) and (1, -5), you can see that the midpoint between them is (1, -2).

Compare your answer with the correct one above

Question

What are the coordinates of the center of the hyperbolic inequality $\frac{[(x+3)^{2}]}{9}-\frac{(y^{2})}{4}< 1$ ?

Answer

The equation for a horizontal hyperbola is $\frac{[(x-h)^{2}]}{(a^{2})}-\frac{[(y-v)^{2}]}{(b^{2})}=1$ . The equation for a vertical hyperbola is $\frac{[(y-v)^{2}]}{(b^{2})}-\frac{[(x-h)^{2}]}{(a^{2})}=1$ . In both, (h, v) is the center of the hyperbola. Hyperbolic inequalities use an inequality sign rather than an equals sign, but otherwise have the same form as hyperbolic equations. Because the two terms are combined using subtraction and the x-term appears first, this inequality represents a horizontal hyperbola. To derive the center of a hyperbola from its equation or inequality, flip the sign of the constants that appear after the x and y in the equation or inequality. The constant following x is 3, so the x-coordinate of the center is -3. No constant follows y, so the y-coordinate of the center is 0.

The graph of the hyperbolic inequality $\frac{[(x-h)^{2}]}{(a^{2})}-\frac{[(y-v)^{2}]}{(b^{2})}=1$ appears as follows:

As you can see, the midpoint between the two vertices of (-6, 0) and (0, 0) is (-3, 0).

Compare your answer with the correct one above

Question

Which equation does this graph represent?

Answer

The equation for a horizontal hyperbola is . The equation for a vertical hyperbola is . In both, (h, v) is the center of the hyperbola. The graph shows a horizontal hyperbola, so in its corresponding equation the x-term must appear first. The center lies at (-2, -1), so x must be followed by the constant 2, and y must be followed by the constant 1. The graph shows a hyperbola rather than an ellipse, so the x- and y-terms must be combined using subtraction rather than addition.

Compare your answer with the correct one above

Tap the card to reveal the answer