Inverse Functions - Algebra II

Card 0 of 20

Question

$f(x) = x^{3} -5$

Which one of the following functions represents the inverse of $f\left ( x \right )?$

A)

B) $\sqrt[3]{x^{3}-5}$

C) $\sqrt[3]{x+5}$

D) $x^{3 } + 5$

E) $x^{3} - 5$

Answer

Given $y = x^{3} - 5$

Hence $x^{3}=y+5$

Interchanging with we get:

$y^{3}=x+5$

Solving for results in $y=\sqrt[3]{x+5}$ .

Compare your answer with the correct one above

Question

$f(x)=\frac{x+3}{x-2}$

Which of the following represents $f^{-1}(x)$ ?

Answer

The question is asking for the inverse function. To find the inverse, first switch input and output -- which is usually easiest if you use notation instead of . Then, solve for .

$f(x)=\frac{x+3}{x-2}$

$y=\frac{x+3}{x-2}$

Here's where we switch:

$x=\frac{y+3}{y-2}$

To solve for , we first have to get it out of the denominator. We do that by multiplying both sides by .

Distribute:

Get all the terms on the same side of the equation:

Factor out a :

Divide by :

$y=\frac{2x+3}{x-1}$

This is our inverse function!

$f^{-1}(x)=\frac{2x+3}{x-1}$

Compare your answer with the correct one above

Question

Find the inverse of .

Answer

To create the inverse, switch x and y making the solution x=3y+3.

y must be isolated to finish the problem.

Compare your answer with the correct one above

Question

Please find the inverse of the following function.

Answer

In order to find the inverse function, we must swap and and then solve for .

Becomes

Now we need to solve for :

$x+\underset{+9}{0}=4y-\underset{+9}{9}$

Finally, we need to divide each side by 4.

$\frac{x+9}{4}=\frac{4y}{4}$

This gives us our inverse function:

$y = \frac{x+9}{4}$

Compare your answer with the correct one above

Question

What is the inverse of the following function?

Answer

Let's say that the function takes the input and yields the output . In math terms:

So, the inverse function needs to take the input and yield the output :

$f^{-1}(b)=a$

So, to answer this question, we need to flip the inputs and outputs for . We do this by replacing with (or a dummy variable; I used ) and with . Then we solve for to get our inverse function:

Now we solve for by subtracting from both sides, taking the cube root, and then adding :

$y=\sqrt[3]{x-3}+4$

is our inverse function, $f^{-1}(x)$

Compare your answer with the correct one above

Question

$g^{-1}(2)=6$

$f^{-1}(-2)=4$

$f^{-1}(9)=2$

What is $f\circ g\circ f^{-1}(6)$ ?

Answer

The question is essentially asking this: take $f^{-1}(6)$ say that equals , then take , then whatever that equals, say , take . So, we start with $f^{-1}(6)$ ; we know that , so if we flip that around we know $f^{-1}(6)=3$ . Now we have to take , but we know that is . Now we have to take , but we don't have that in our table; we do have $f^{-1}(-2)=4$ , though, and if we flip it around, we get , which is our answer.

Compare your answer with the correct one above

Question

$g^{-1}(2)=6$

$f^{-1}(-2)=4$

$f^{-1}(9)=2$

What is $g\circ f\circ g^{-1}(4)$ ?

Answer

Our question is asking "What is of of inverse?" First we find the inverse of . Looking at the question, we see ; if we flip that around, we get $g^{-1}(4)=3$ . Now we need to find what is; that is an easy one, as it is directly provided: . Now we need to find . Again, this isn't given, but what is given is $g^{-1}(2)=6$ , so , and that is our answer.

Compare your answer with the correct one above

Question

Over which line do you flip a function when finding its inverse?

Answer

To find the inverse of a function, you need to change all of the values to values and all the values to values. If you flip a function over the line , then you are changing all the values to values and all the values to values, giving you the inverse of your function.

Compare your answer with the correct one above

Question

Find the inverse of this function:

$f(x)=e^{x^2-3}+\pi$

Answer

To find the inverse of a function, we need to switch all the inputs ( variables) for all the outputs ( variables or variables), so if we just switch all the variables to variables and all the variables to variables and solve for , then will be our inverse function.

$f(x)=e^{x^2-3}+\pi$

turns into the following once the variables are switched:

$x=e^{y^2-3}+\pi$

the first thing we do is subtract $\pi$ from each side; then, we take the natural log of each side. This gives us

$ln(x-\pi)=y^2-3$

Then we just add three to each side and take the square root of each side, making sure we have both the positive and negative roots.

$\pm\sqrt{ln(x-\pi)+3}=y$

This is the inverse function of the function with which we were provided.

Compare your answer with the correct one above

Question

What is the inverse of $y=\frac{2}{5}x -3$ ?

Answer

Interchange the and variables and solve for .

$x=\frac{2}{5}y -3$

$x+3=\frac{2}{5}y$

$y=\frac{5}{2}x+\frac{15}{2}$

Compare your answer with the correct one above

Question

Inverse Functions

Given the function below, find its inverse:

Answer

When finding the inverse go through the following steps:

Replace f(x) with y:

Swap the x and y variables

Solve for y:

add 5 to both sides

divide everything by 3

$f^{^{-1}}(x)=\frac{1}{3}x+\frac{5}{3}$ simplify and express as an inverse using $f^{-1}(x)$

Compare your answer with the correct one above

Question

Find the inverse of .

Answer

To find the inverse of a function, swap the x and y variable and solve for y.

The new expression after the swap is

Now solve for y.

$y^2=\frac{x-7}{3}$

$y=\pm\sqrt{\frac{x-7}{3}}$

This y actually represents the inverse of the original y.

Compare your answer with the correct one above

Question

What is the inverse of the following function?

$f(x)=-2+\sqrt{x-1}$

Answer

To find the inverse of a function, switch the x and y in the original function and then solve for y.

$f(x)=-2+\sqrt{x-1}$

$y=-2+\sqrt{x-1}$

$x=-2+\sqrt{y-1}$

$x+2=\sqrt{y-1}$

$(x+2)^{2}=(\sqrt{y-1})^{2}$

$(x+2)^{2}=y-1$

$y=(x+2)^{2}+1$

$y=x^{2}+4x+5$

Compare your answer with the correct one above

Question

Find the inverse of .

Answer

In order to find the inverse, interchange the and variables.

Solve for . Add eight on both sides.

Divide by three on both sides.

$\frac{x+8}{3}=\frac{3y}{3}$

Simplify the left and right side.

The answer is: $y= \frac{1}{3}x+\frac{8}{3}$

Compare your answer with the correct one above

Question

Find the inverse of:

Answer

Interchange the and variables in the equation.

Solve for . Subtract two on both sides.

Distribute the right side of the equation to eliminate the parentheses.

Subtract four on both sides.

Divide by negative two on both sides.

$\frac{x-6}{-2}=y$

Rewrite this in slope-intercept form.

The answer is: $y= -\frac{1}{2}x + 3$

Compare your answer with the correct one above

Question

If , find $f^{-1}(x)$ .

Answer

The notation $f^{-1}(x)$ denotes the inverse of the function .

Rewrite using as a replacement of .

Interchange and and solve for .

Divide by four on both sides.

$\frac{x}{4}=y^2$

Square root both sides to eliminate the squared term.

$y=\pm \sqrt{\frac{x}{4}} = \pm\frac{ \sqrt x}{2}$

The answer is: $y=\pm\frac{ \sqrt x}{2}$

Compare your answer with the correct one above

Question

Choose the inverse of $y=\frac{x-3}{2}$ .

Answer

To find the inverse of a linear function, switch the variables and solve for y.

$y=\frac{x-3}{2}$

Switch the variables:

$x=\frac{y-3}{2}$

Multiply both sides by 2:

Add 3 to both sides to isolate y:

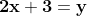
$\mathbf{2x+3=y}$

Compare your answer with the correct one above

Question

Find the inverse of

Answer

Combine the x terms:

Switch the variables:

Solve for y:

Convert y term to a fraction to see how to simplify more easily:

$x+5=\frac{5}{2}y$

$\mathbf{y=\frac{2(x+5)}{5}}$

Compare your answer with the correct one above

Question

Find the inverse function of $6x-\frac{2}{3}y=4$ .

Answer

$6x-\frac{2}{3}y=4$

First convert to slope intercept form:

To find the inverse we switch the variables and solve for y again:

$\mathbf{y=\frac{x+6}{9}}$

Compare your answer with the correct one above

Question

Find the inverse function and simplify your solution:

Answer

To find the Inverse function of:

1. Replace with :

2. Switch the variables and :

3. Solve for :

$y = \frac{x - 21}{3}$

4. Simplify:

$y = \frac{1}{3}x - 7$

5. Replace with $f^{-1}(x)$ and the final solution is:

$f^{-1}(x) = \frac{1}{3}x - 7$

Compare your answer with the correct one above

Tap the card to reveal the answer