Graphing Absolute Value Functions - Algebra II
Card 0 of 7
What is the equation of the above function?
What is the equation of the above function?
The formula of an absolute value function is 
where m is the slope, a is the horizontal shift and b is the vertical shift. The slope can be found with any two adjacent integer points, e.g. 
and 
, and plugging them into the slope formula, 
, yielding 
. The vertical and horizontal shifts are determined by where the crux of the absolute value function is. In this case, at 
, and those are your a and b, respectively.
The formula of an absolute value function is
Compare your answer with the correct one above
Refer to the above figure.
Which of the following functions is graphed?
Refer to the above figure.
Which of the following functions is graphed?
Below is the graph of 
:
The given graph is the graph of 
translated by moving the graph 7 units left (that is, 
unit right) and 2 units down (that is, 
units up)
The function graphed is therefore
where 
. That is,
Below is the graph of
The given graph is the graph of
The function graphed is therefore
Compare your answer with the correct one above
Refer to the above figure.
Which of the following functions is graphed?
Refer to the above figure.
Which of the following functions is graphed?
Below is the graph of :
The given graph is the graph of 
reflected in the 
-axis, then translated left 2 units (or, equivalently, right 
units. This graph is
, where 
.
The function graphed is therefore
Below is the graph of
The given graph is the graph of
The function graphed is therefore
Compare your answer with the correct one above
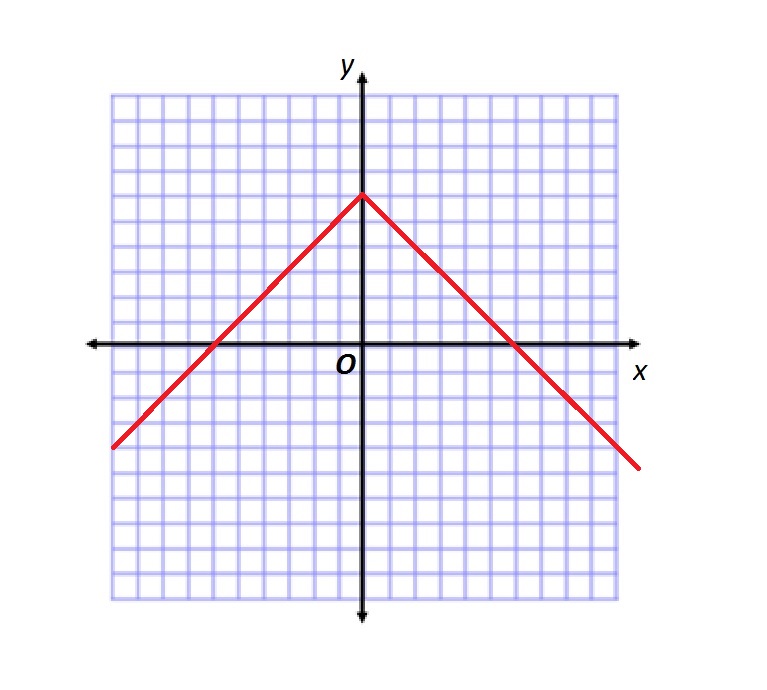
Refer to the above figure.
Which of the following functions is graphed?
Refer to the above figure.
Which of the following functions is graphed?
Below is the graph of :
The given graph is the graph of reflected in the -axis, then translated up 6 units. This graph is
, where 
.
The function graphed is therefore
Below is the graph of
The given graph is the graph of
The function graphed is therefore
Compare your answer with the correct one above
Which of the following absolute value functions is represented by the following graph?
Which of the following absolute value functions is represented by the following graph?
The equation can be determined from the graph by following the rules of transformations; the base equation is:
The graph of this base equation is:
When we compare our graph to the base equation graph, we see that it has been shifted right 3 units, up 1 unit, and our graph has been stretched vertically by a factor of 2. Following the rules of transformations, the equation for our graph is written as:
The equation can be determined from the graph by following the rules of transformations; the base equation is:
The graph of this base equation is:
When we compare our graph to the base equation graph, we see that it has been shifted right 3 units, up 1 unit, and our graph has been stretched vertically by a factor of 2. Following the rules of transformations, the equation for our graph is written as:
Compare your answer with the correct one above
Give the vertex of the graph of the function 
.
Give the vertex of the graph of the function
Let 
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates 
. In terms of 
,
The graph of this function can be formed by shifting the graph of 
left 6 units (
) and down 7 units (
). The vertex is therefore located at 
.
Let
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates
The graph of this function can be formed by shifting the graph of
Compare your answer with the correct one above
Give the vertex of the graph of the function 
.
Give the vertex of the graph of the function
Let 
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates 
. In terms of 
,
,
or, alternatively written,
The graph of 
is the same as that of 
, after it shifts 10 units left ( 
), it flips vertically (negative symbol), and it shifts up 10 units (the second 
). The flip does not affect the position of the vertex, but the shifts do; the vertex of the graph of 
is at 
.
Let
The graph of this basic absolute value function is a "V"-shaped graph with a vertex at the origin, or the point with coordinates
or, alternatively written,
The graph of
Compare your answer with the correct one above