Polynomial Functions - Algebra II
Card 0 of 20
Which equation best represents the following graph?
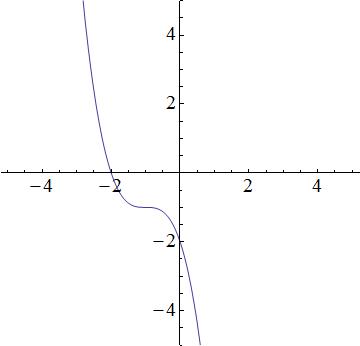
Which equation best represents the following graph?

We have the following answer choices.




The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.
We have the following answer choices.
The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.
Compare your answer with the correct one above
For the graph below, match the graph b with one of the following equations:








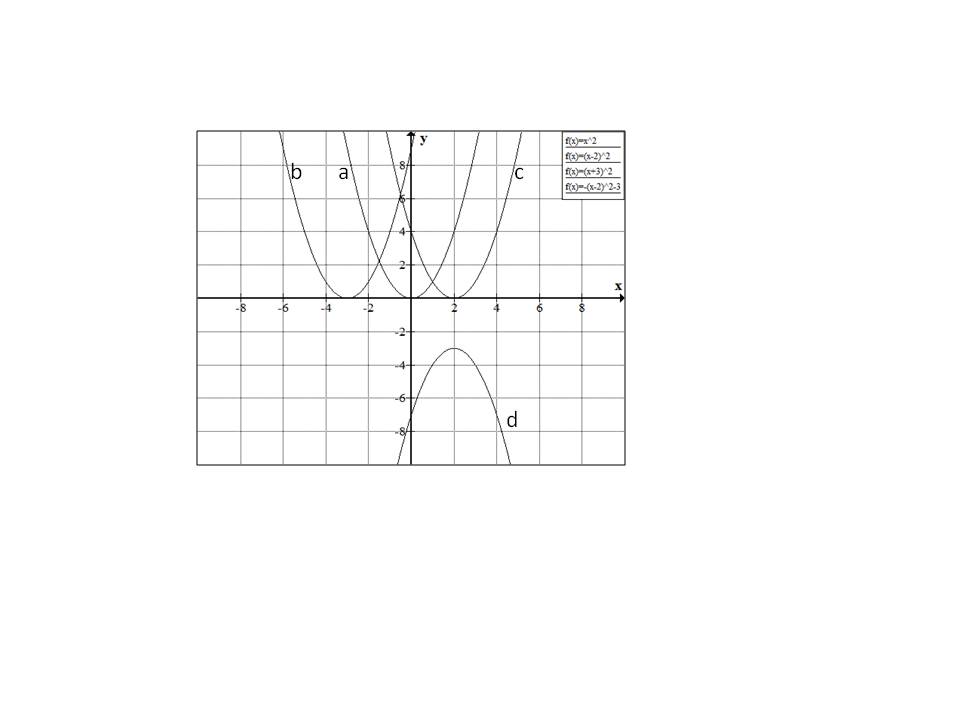
For the graph below, match the graph b with one of the following equations:





Starting with 
 moves the parabola
moves the parabola  by
by  units to the right.
units to the right.
Similarly  moves the parabola by
moves the parabola by  units to the left.
units to the left.
Hence the correct answer is option  .
.
Starting with



Similarly 

Hence the correct answer is option 
Compare your answer with the correct one above
Which of the graphs best represents the following function?

Which of the graphs best represents the following function?

The highest exponent of the variable term is two ( ). This tells that this function is quadratic, meaning that it is a parabola.
). This tells that this function is quadratic, meaning that it is a parabola.
The graph below will be the answer, as it shows a parabolic curve.

The highest exponent of the variable term is two (
The graph below will be the answer, as it shows a parabolic curve.

Compare your answer with the correct one above

Where does the graph of  cross the
cross the  axis?
axis?
Where does the graph of 

To find where the graph crosses the horizontal axis, we need to set the function equal to 0, since the  value at any point along the
value at any point along the  axis is always zero.
axis is always zero.


To find the possible rational zeroes of a polynomial, use the rational zeroes theorem:

Our constant is 10, and our leading coefficient is 1. So here are our possible roots:

Let's try all of them and see if they work! We're going to substitute each value in for  using synthetic substitution. We'll try -1 first.
using synthetic substitution. We'll try -1 first.

Looks like that worked! We got 0 as our final answer after synthetic substitution. What's left in the bottom row helps us factor  down a little farther:
down a little farther:

We keep doing this process until  is completely factored:
is completely factored:

Thus,  crosses the
crosses the  axis at
axis at  .
.
To find where the graph crosses the horizontal axis, we need to set the function equal to 0, since the 

To find the possible rational zeroes of a polynomial, use the rational zeroes theorem:
Our constant is 10, and our leading coefficient is 1. So here are our possible roots:
Let's try all of them and see if they work! We're going to substitute each value in for 
Looks like that worked! We got 0 as our final answer after synthetic substitution. What's left in the bottom row helps us factor 
We keep doing this process until 
Thus, 


Compare your answer with the correct one above

Where does  cross the
cross the  axis?
axis?
Where does 

 crosses the
crosses the  axis when
axis when  equals 0. So, substitute in 0 for
equals 0. So, substitute in 0 for  :
:







Compare your answer with the correct one above

Which of the following is an equation for the above parabola?

Which of the following is an equation for the above parabola?
The zeros of the parabola are at  and
and  , so when placed into the formula
, so when placed into the formula
 ,
,
each of their signs is reversed to end up with the correct sign in the answer. The coefficient can be found by plugging in any easily-identifiable, non-zero point to the above formula. For example, we can plug in  which gives
which gives



The zeros of the parabola are at 


each of their signs is reversed to end up with the correct sign in the answer. The coefficient can be found by plugging in any easily-identifiable, non-zero point to the above formula. For example, we can plug in 
Compare your answer with the correct one above
Turns on a polynomial graph.
What is the maximum number of turns the graph of the below polynomial function could have?

Turns on a polynomial graph.
What is the maximum number of turns the graph of the below polynomial function could have?
When determining the maximum number of turns a polynomial function might have, one must remember:
Max Number of Turns for Polynomial Function = degree - 1
First, we must find the degree, in order to determine the degree we must put the polynomial in standard form, which means organize the exponents in decreasing order:

Now that f(x) is in standard form, the degree is the largest exponent, which is 8.
We now plug this into the above:
Max Number of Turns for Polynomial Function = degree - 1
Max Number of Turns for Polynomial Function = 8 - 1
which is 7.
The correct answer is 7.
When determining the maximum number of turns a polynomial function might have, one must remember:
Max Number of Turns for Polynomial Function = degree - 1
First, we must find the degree, in order to determine the degree we must put the polynomial in standard form, which means organize the exponents in decreasing order:
Now that f(x) is in standard form, the degree is the largest exponent, which is 8.
We now plug this into the above:
Max Number of Turns for Polynomial Function = degree - 1
Max Number of Turns for Polynomial Function = 8 - 1
which is 7.
The correct answer is 7.
Compare your answer with the correct one above
End Behavior
Determine the end behavior for  below:
below:

End Behavior
Determine the end behavior for 
In order to determine the end behavior of a polynomial function, it must first be rewritten in standard form. Standard form means that the function begins with the variable with the largest exponent and then ends with the constant or variable with the smallest exponent.
For f(x) in this case, it would be rewritten in this way:

When this is done, we can see that the function is an Even (degree, 4) Negative (leading coefficent, -3) which means that both sides of the graph go down infinitely.
In order to answer questions of this nature, one must remember the four ways that all polynomial graphs can look:
Even Positive:

Even Negative:

Odd Positive:

Odd Negative:

In order to determine the end behavior of a polynomial function, it must first be rewritten in standard form. Standard form means that the function begins with the variable with the largest exponent and then ends with the constant or variable with the smallest exponent.
For f(x) in this case, it would be rewritten in this way:
When this is done, we can see that the function is an Even (degree, 4) Negative (leading coefficent, -3) which means that both sides of the graph go down infinitely.
In order to answer questions of this nature, one must remember the four ways that all polynomial graphs can look:
Even Positive:
Even Negative:
Odd Positive:
Odd Negative:
Compare your answer with the correct one above
Which of the following is a graph for the following equation:

Which of the following is a graph for the following equation:
The way to figure out this problem is by understanding behavior of polynomials.
The sign that occurs before the  is positive and therefore it is understood that the function will open upwards. the "8" on the function is an even number which means that the function is going to be u-shaped. The only answer choice that fits both these criteria is:
is positive and therefore it is understood that the function will open upwards. the "8" on the function is an even number which means that the function is going to be u-shaped. The only answer choice that fits both these criteria is:

The way to figure out this problem is by understanding behavior of polynomials.
The sign that occurs before the 

Compare your answer with the correct one above
When we look at the function we see that the highest power of the function is a 3 which means it is an "odd degree" function. This means that the right and left side of the function will approach opposite directions. *Remember O for Odd and O for opposite.
In this case we also have a negative sign associated with the highest power portion of the function - this means that the function is flipped.
Both of these combine to make this an "odd negative" function.
Odd negative functions always have the right side of the function approaching down and the left side approaching up.
We represent this mathematically by saying that as x approaches negative infinity (left side), the function will approach positive infinity:

...and as x approaches positive infinity (right side) the function will approach negative infinity:

When we look at the function we see that the highest power of the function is a 3 which means it is an "odd degree" function. This means that the right and left side of the function will approach opposite directions. *Remember O for Odd and O for opposite.
In this case we also have a negative sign associated with the highest power portion of the function - this means that the function is flipped.
Both of these combine to make this an "odd negative" function.
Odd negative functions always have the right side of the function approaching down and the left side approaching up.
We represent this mathematically by saying that as x approaches negative infinity (left side), the function will approach positive infinity:
...and as x approaches positive infinity (right side) the function will approach negative infinity:
Compare your answer with the correct one above



Then set each factor equal to zero, if any of the ( ) equal zero, then the whole thing will equal zero because of the zero product rule.


Then set each factor equal to zero, if any of the ( ) equal zero, then the whole thing will equal zero because of the zero product rule.
Compare your answer with the correct one above
 is a polynomial function.
is a polynomial function.  ,
,  .
.
True or false: By the Intermediate Value Theorem,  cannot have a zero on the interval
cannot have a zero on the interval  .
.



True or false: By the Intermediate Value Theorem, 

As a polynomial function, the graph of  is continuous. By the Intermediate Value Theorem, if
is continuous. By the Intermediate Value Theorem, if  or
or  , then there must exist a value
, then there must exist a value  such that
such that  .
.
Set  and
and  . It is not true that
. It is not true that  , so the Intermediate Value Theorem does not prove that there exists
, so the Intermediate Value Theorem does not prove that there exists  such that
such that  . However, it does not disprove that such a value exists either. For example, observe the graphs below:
. However, it does not disprove that such a value exists either. For example, observe the graphs below:

Both are polynomial graphs fitting the given conditions, but the only the equation graphed at right has a zero on  .
.
As a polynomial function, the graph of 




Set 





Both are polynomial graphs fitting the given conditions, but the only the equation graphed at right has a zero on 
Compare your answer with the correct one above
 is a polynomial function.
is a polynomial function.  ,
,  .
.
True, false, or undetermined:  has a zero on the interval
has a zero on the interval  .
.



True, false, or undetermined: 

As a polynomial function, the graph of  is continuous. By the Intermediate Value Theorem (IVT), if
is continuous. By the Intermediate Value Theorem (IVT), if  or
or  , then there must exist a value
, then there must exist a value  such that
such that  .
.
Setting  , and examining the first condition, the above becomes:
, and examining the first condition, the above becomes:
if  , then there must exist a value
, then there must exist a value  such that
such that  - or, restated,
- or, restated,  must have a zero on the interval
must have a zero on the interval  . Since
. Since  ,
,  . the condition holds, and by the IVT, it follows that
. the condition holds, and by the IVT, it follows that  has a zero on
has a zero on  .
.
As a polynomial function, the graph of 




Setting 
if 








Compare your answer with the correct one above
 is a polynomial function.
is a polynomial function.  , and
, and  has a zero on the interval
has a zero on the interval  .
.
True or false: By the Intermediate Value Theorem, 




True or false: By the Intermediate Value Theorem,
As a polynomial function, the graph of  is continuous. By the Intermediate Value Theorem, if
is continuous. By the Intermediate Value Theorem, if  or
or  , then there must exist a value
, then there must exist a value  such that
such that  .
.
Setting  ,
,  and
and  , this becomes: If
, this becomes: If  or
or  , then there must exist a value
, then there must exist a value  such that
such that  - that is,
- that is,  must have a zero on
must have a zero on  .
.
However, the question is asking us to use the converse of this statement, which is not true in general. If  has a zero on
has a zero on  , it does not necessarily follow that
, it does not necessarily follow that  or
or  - specifically, with
- specifically, with  , it does not necessarily follow that
, it does not necessarily follow that  . A counterexample is the function shown below, which fits the conditions of the problem but does not have a negative value for
. A counterexample is the function shown below, which fits the conditions of the problem but does not have a negative value for  :
:

The answer is false.
As a polynomial function, the graph of 




Setting 








However, the question is asking us to use the converse of this statement, which is not true in general. If 







The answer is false.
Compare your answer with the correct one above
 is a polynomial function. The graph of
is a polynomial function. The graph of  has no
has no  -intercepts; its
-intercepts; its  -intercept of the graph is at
-intercept of the graph is at  .
.
True or false: By the Intermediate Value Theorem,  has no negative values.
has no negative values.





True or false: By the Intermediate Value Theorem, 
As a polynomial function, the graph of  is continuous. By the Intermediate Value Theorem, if
is continuous. By the Intermediate Value Theorem, if  or
or  , then there must exist a value
, then there must exist a value  such that
such that  .
.
Setting  and
and  , assuming for now that
, assuming for now that  , and looking only at the second condition, this statement becomes: If
, and looking only at the second condition, this statement becomes: If  , then there must exist a value
, then there must exist a value  such that
such that  - or, equivalently,
- or, equivalently,  must have a zero on
must have a zero on  .
.
However, the conclusion of this statement is false:  has no zeroes at all. Therefore,
has no zeroes at all. Therefore,  is false, and
is false, and  has no negative values for any
has no negative values for any  . By similar reasoning,
. By similar reasoning,  has no negative values for any
has no negative values for any  . Therefore, by the IVT, by way of its contrapositive, we have proved that
. Therefore, by the IVT, by way of its contrapositive, we have proved that  is positive everywhere.
is positive everywhere.
As a polynomial function, the graph of 




Setting 







However, the conclusion of this statement is false: 






Compare your answer with the correct one above
How many  -intercepts does the graph of the function
-intercepts does the graph of the function

have?
How many 
have?
The graph of a quadratic function  has an
has an  -intercept at any point
-intercept at any point  at which
at which  , so we set the quadratic expression equal to 0:
, so we set the quadratic expression equal to 0:

Since the question simply asks for the number of  -intercepts, it suffices to find the discriminant of the equation and to use it to determine this number. The discriminant of the quadratic equation
-intercepts, it suffices to find the discriminant of the equation and to use it to determine this number. The discriminant of the quadratic equation

is
 .
.
Set  , and evaluate:
, and evaluate:

The discriminant is positive, so the  has two real zeroes - and its graph has two
has two real zeroes - and its graph has two  -intercepts.
-intercepts.
The graph of a quadratic function 



Since the question simply asks for the number of 
is

Set 
The discriminant is positive, so the 

Compare your answer with the correct one above
The vertex of the graph of the function

appears in __________.
The vertex of the graph of the function
appears in __________.
The graph of the quadratic function  is a parabola with its vertex at the point with coordinates
is a parabola with its vertex at the point with coordinates
 .
.
Set  ; the
; the  -coordinate is
-coordinate is  .
.
Evaluate  by substitution:
by substitution:




The vertex has a negative  -coordinate and a negative
-coordinate and a negative  -coordinate, putting it in the lower left quadrant, or Quadrant III.
-coordinate, putting it in the lower left quadrant, or Quadrant III.
The graph of the quadratic function 

Set 


Evaluate 
The vertex has a negative 

Compare your answer with the correct one above
The vertex of the graph of the function

appears in __________.
The vertex of the graph of the function
appears in __________.
The graph of the quadratic function  is a parabola with its vertex at the point with coordinates
is a parabola with its vertex at the point with coordinates
 .
.
Set  ; the
; the  -coordinate is
-coordinate is
 .
.
Evaluate  by substitution:
by substitution:




The vertex has a positive  -coordinate and a positive
-coordinate and a positive  -coordinate, putting it in the upper right quadrant, or Quadrant I.
-coordinate, putting it in the upper right quadrant, or Quadrant I.
The graph of the quadratic function 

Set 


Evaluate 
The vertex has a positive 

Compare your answer with the correct one above
The vertex of the graph of the function

appears ________
The vertex of the graph of the function
appears ________
The graph of the quadratic function  is a parabola with its vertex at the point with coordinates
is a parabola with its vertex at the point with coordinates
 .
.
Set  ; the
; the  -coordinate is
-coordinate is

Evaluate  by substitution:
by substitution:




The vertex has 0 as its  -coordinate; it is therefore on an axis.
-coordinate; it is therefore on an axis.
The graph of the quadratic function 

Set 

Evaluate 
The vertex has 0 as its 
Compare your answer with the correct one above
How many  -intercepts does the graph of the following function have?
-intercepts does the graph of the following function have?

How many 
The graph of a quadratic function  has an
has an  -intercept at any point
-intercept at any point  at which
at which  , so, first, set the quadratic expression equal to 0:
, so, first, set the quadratic expression equal to 0:

The number of  -intercepts of the graph is equal to the number of real zeroes of the above equation, which can be determined by evaluating the discriminant of the equation,
-intercepts of the graph is equal to the number of real zeroes of the above equation, which can be determined by evaluating the discriminant of the equation,  . Set
. Set  , and evaluate:
, and evaluate:

The discriminant is equal to zero, so the quadratic equation has one real zero, and the graph of  has exactly one
has exactly one  -intercept.
-intercept.
The graph of a quadratic function 



The number of 


The discriminant is equal to zero, so the quadratic equation has one real zero, and the graph of 

Compare your answer with the correct one above


