Statistical Concepts Flashcards - Algebra II

Question

The number of runs scored per game by a little league baseball team is represented by the following frequency distribution:

Number of Runs Scored Frequency
0 5
1 2
2 7
3 9
4 3
5 0
6 4
7 2
8 2
9 1

Using this frequency table, select the correct answer of m ean runs scored by the little league team (rounded to the nearest hundredth).

Number of Runs Scored	Frequency
0	5
1	2
2	7
3	9
4	3
5	0
6	4
7	2
8	2
9	1

Answer

Number of Runs Scored Frequency
0 5
1 2
2 7
3 9
4 3
5 0
6 4
7 2
8 2
9 1

To determine the mean, first the data set should be re-written in sequential order:

The formula to determine mean is:

$\bar{x}=\frac{\sum x}{n}=\frac{118}{35}\approx3.37$

The mean is approximately 3.37 runs scored per game.

Number of Runs Scored	Frequency
0	5
1	2
2	7
3	9
4	3
5	0
6	4
7	2
8	2
9	1

Compare your answer with the correct one above

Question

Thousands of people in the United States were surveyed about their grandparents. This frequency table shows their answer to the question "how many of your grandparents were born outside of the US?

Of the people who had at least one grandparent born outisde of the US, what percent had exactly 3 non-US born grandparents?

Answer

Adding up the total number of grandparents that were born outside the U.S. is our first step in solving this problem.

There are

people who said they had at least 1 grandparent born outside of the US. Of those, only 976 had exactly 3.

So

$\frac{976}{15,631} = 0.062$ or is the answer.

Compare your answer with the correct one above

Question

Thousands of people in the United States were surveyed about their grandparents. This frequency table shows their answer to the question "how many of your grandparents were born outside of the US?"

Is this data normally distributed?

Answer

No - normally distributed data has a low frequency of responses at the high and low ends. Also, the majority of the data is in the middle.

In this data set, the majority of people said "0," and the fewest people said "3" which is near the middle of the data. If this data was normally distributed we would have a higher frequency between 1 and 3 and much lower values for 0 and 4.

Compare your answer with the correct one above

Question

What is the correct frequency distribution for this data set?

1 3 5 2 5 2 4 1 5
2 4 1 2 3 5 5 2 3
3 1 4 4 6 2 3 2 4

Answer

Count the number of times each number appears in the data set.

The number 1 appears 4 times, so the first line is .

Then number 2 appears 7 times, so the next line is .

Continuing in this fashion we see that the numbers 3, 4, and 5 appears 5 times and 6 appears once.

Therefore combining these together we get the following answer:

$\begin{matrix} 1 | 4 \ 2 | 7 \ 3 | 5 \ 4 | 5 \ 5 | 5 \ 6 | 1 \end{matrix}$

Compare your answer with the correct one above

Question

What is the mean of the data in this frequency table?

# Frequency
1 3
2 4
3 0
4 2

Answer

The frequency table represents the data set:

1, 1, 1, 2, 2, 2, 2, 4, 4.

The sum is 19 and there are 9 data points, so the mean is

$\frac{19}{9} = 2.11$ .

Compare your answer with the correct one above

Question

What is the median of the data in this frequency table?

# Frequency
1 3
2 4
3 0
4 2

Answer

The frequency table represents the data set:

1, 1, 1, 2, 2, 2, 2, 4, 4.

The median is 2 because 4 data points appear before and after the center 2.

Compare your answer with the correct one above

Question

Which frequency table has a median of 5? (The first column represents the data points, the second column the frequency)

Answer

The correct frequency table represents the data set 3, 4, 5, 5, 6, 6, 8.

Since there are 7 data points our median will be the 4th spot which makes the value 5. It occures at the 4th spot because at that spot half the data points are below it while the other half are above it.

The center number of that data set is 5 as required.

Compare your answer with the correct one above

Question

Find the 85th percentile score in the following test results.

{95, 88, 70, 75, 83, 70, 66, 91, 68, 76, 82}

Answer

{95, 88, 70, 75, 83, 70, 66, 91, 68, 76, 82}

Arrange the values in numerical order.

{66, 68, 70, 70, 75, 76, 82, 83, 88, 91, 95}

Use the following to calculate percentile-

$i=(\frac{p}{100})n$

where is the percentile and is the number of data in the set

$i=(\frac{85}{100})11$

This number gives of the location of the 85th percentile in our ordered set. Since it is not a whole number, round up, which will give us 10.

The 85th percentile score is the 10th value in our set, which is 91.

Compare your answer with the correct one above

Question

Above is the stem-and-leaf display for a group of test scores. Which of the following scores would come closest to being at the $35^{th}$ percentile?

Answer

The stem-and-leaf display represents 53 scores. The score at the 35th percentile would be the score that is greater than 35% of the scores, or

$53 \times 0.35 \approx 18.5$ scores.

Rounding, we count 19 scores from the bottom:

The score represented is 64, which is the correct response.

Compare your answer with the correct one above

Question

Above is the stem-and-leaf display for a group of test scores. At what percentile would the student who made a score of 86 be?

Answer

The stem-and-leaf display represents 53 scores. The "stems" (or left column) represent the tens digits, and the "leaves" in each row represent units digits, so the scores are

The student who scored an 86 outscored 42 of the students, or

$\frac{42}{53} \times 100 % \approx 79.2 %$

of them. Since percentile is given to the nearest whole number, the correct response is 79.

Compare your answer with the correct one above

Question

If a student is ranked eight out of ten in a competition, what is the student's percentile rank?

Answer

The formula to calculate a percentile rank is: $\frac{x}{n}\cdot100$

where represents total of scores below the rank, and is the total number of competitors.

Substitute the values into the formula.

$\frac{2}{10}\cdot100 = 20$

Compare your answer with the correct one above

Question

The times for a six-mile race are shown below.

Sean: hours

Ankur: hours

Sarah: hours

Fred: hours

Ron: hours

Jareth: hours

Determine which percentile Sean's time is in.

Answer

First arrange the runners in order of fastest to slowest times:

Ron

Sarah

Jareth

Sean

Ankur

Fred

There are six runners so there will be six different percentiles, each seperated by $100/6\approx 16.6667$ percent. A person's percentile refers to which percentage of times are below that person's time. For example, Ron's time is better than percent of all runners, so he is in the rd percentile.

Then each runner is in the following percentiles:

Ron - rd

Sarah - th

Jareth - th

Sean - rd

Ankur - th

Fred - th

As you can see, Sean is in the rd percentile.

Compare your answer with the correct one above

Question

In a litter of nine kittens, the only orange kitten weighs more than three in the litter, and less than the other remaining five.

What is the percentile of the orange kitten's weight in comparison to the litter?

Answer

The percentile is equal to how many items in the set are equal to or less than the one in question divided by the total number of items in the set.

Because there are four items equal to or less than the orange kitten's weight and there are nine items total in the set, the percentile is equal to

$\frac{4}{9}$ or

Compare your answer with the correct one above

Question

98, 99, 99, 100, 101, 102, 104, 104, 105, 105, 107, 110, 112, 112

For the above data set, 102 is in what percentile?

Answer

In the data set, 102 is the 6th data point listed. There are 14 data points total. This means that $6 \div 14 \approx 0.4286 = 42.86$ % of the data is at or below 102. That's approximately the 43rd percentile.

Compare your answer with the correct one above

Question

98, 99, 99, 100, 101, 102, 104, 104, 105, 105, 107, 110, 112, 112

For the above data set, 110 is in what percentile?

Answer

The number 110 is the 12th in the list of 14 data points. That means that $12 \div 14 \approx 0.857 = 85.7$ %. Since about 86% of the data points are at or below 110, it's in the 86th percentile.

Compare your answer with the correct one above

Question

Given the following set of data, what is twice the interquartile range?

Answer

How do you find the interquartile range?

We can find the interquartile range or IQR in four simple steps:

Order the data from least to greatest

Find the median

Calculate the median of both the lower and upper half of the data

The IQR is the difference between the upper and lower medians

Step 1: Order the data

In order to calculate the IQR, we need to begin by ordering the values of the data set from the least to the greatest. Likewise, in order to calculate the median, we need to arrange the numbers in ascending order (i.e. from the least to the greatest).

Let's sort an example data set with an odd number of values into ascending order.

$\textup{Odd data set}: 9, 3, 2, 5, 6, 11, 4, 3, 2$

$\textup{Odd data set (ascending)}: 2, 2, 3, 3, 4, 5, 6, 9, 11$

Now, let's perform this task with another example data set that is comprised of an even number of values.

$\textup{Even data set}: 11, 2, 4, 3, 8, 1, 2, 7, 4, 9$

Rearrange into ascending order.

$\textup{Even data set (ascending)}: 1, 2, 2, 3, 4, 4, 7, 8, 9, 11$

Step 2: Calculate the median

Next, we need to calculate the median. The median is the "center" of the data. If the data set has an odd number of data points, then the mean is the centermost number. On the other hand, if the data set has an even number of values, then we will need to take the arithmetic average of the two centermost values. We will calculate this average by adding the two numbers together and then dividing that number by two.

First, we will find the median of a set with an odd number of values. Cross out values until you find the centermost point

$\textup{Odd data set}: ot{2}, ot{2}, ot{3}, ot{3}, {\color{Red} 4}, ot{5}, ot{6}, ot{9}, ot{11}$

The median of the odd valued data set is four.

Now, let's find the mean of the data set with an even number of values. Cross out values until you find the two centermost points and then calculate the average the two values.

$\textup{Even data set}: ot{1}, ot{2}, ot{2}, ot{3}, {\color{Red} 4}, {\color{Red} 4}, ot{7}, ot{8}, ot{9}, ot{11}$

Find the average of the two centermost values.

$\textup{Average}=\frac{4+4}{2}$

$\textup{Average}=\frac{8}{2}$

$\textup{Average}=4$

The median of the even valued set is four.

Step 3: Upper and lower medians

Once we have found the median of the entire set, we can find the medians of the upper and lower portions of the data. If the data set has an odd number of values, we will omit the median or centermost value of the set. Afterwards, we will find the individual medians for the upper and lower portions of the data.

$\textup{Odd data set}: 2, 2, 3, 3, 4, 5, 6, 9, 11$

Omit the centermost value.

$\textup{Odd data set}: 2, 2, 3, 3,\mid 5, 6, 9, 11$

Find the median of the lower portion.

$\textup{Odd data set}: ot{2}, {\color{Red} 2}, {\color{Red} 3}, ot{3},\mid 5, 6, 9, 11$

Calculate the average of the two values.

$\textup{Average}=\frac{2+3}{2}$

$\textup{Average}=\frac{5}{2}$

$\textup{Average}=2.5$

The median of the lower portion is

Find the median of the upper portion.

$\textup{Odd data set}: 2, 2, 3, 3,\mid ot{5}, {\color{Red} 6}, {\color{Red} 9}, ot{11}$

Calculate the average of the two values.

$\textup{Average}=\frac{6+9}{2}$

$\textup{Average}=\frac{15}{2}$

$\textup{Average}=7.5$

The median of the upper potion is

If the data set has an even number of values, we will use the two values used to calculate the original median to divide the data set. These values are not omitted and become the largest value of the lower data set and the lowest values of the upper data set, respectively. Afterwards, we will calculate the medians of both the upper and lower portions.

$\textup{Even data set}: 1, 2, 2, 3, 4\mid 4, 7, 8, 9, 11$

Find the median of the lower portion.

$\textup{Even data set}: ot{1}, ot{2}, {\color{Red} 2}, ot{3}, ot{4}\mid 4, 7, 8, 9, 11$

The median of the lower portion is two.

Find the median of the upper portion.

$\textup{Even data set}: 1, 2, 2, 3, 4\mid ot{4}, ot{7}, {\color{Red} 8}, ot{9}, ot{11}$

The median of the upper portion is eight.

Step 4: Calculate the difference

Last, we need to calculate the difference of the upper and lower medians by subtracting the lower median from the upper median. This value equals the IQR.

Let's find the IQR of the odd data set.

$\textup{IQR of the odd data set}=7.5-2.5$

$\textup{IQR}=5$

Finally, we will find the IQR of the even data set.

$\textup{IQR of the even data set}=8-2$

$\textup{IQR}=6$

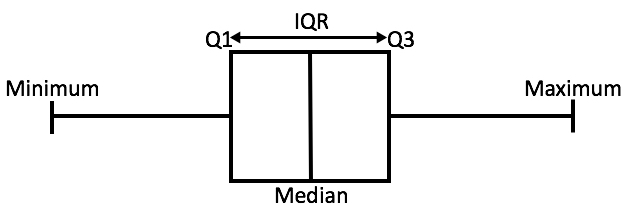
In order to better illustrate these values, their positions in a box plot have been labeled in the provided image.

Now that we have solved a few examples, let's use this knowledge to solve the given problem.

Solution:

First, we need to put the data in order from smallest to largest.

$Q_{2}$ = median of the overall data set

$Q_{1}$ = median of the lower half of the data

$Q_{3}$ = median of the upper half of the data

$Q_{2} = 32$

is the overall median, leaving as the lower half of the data and as the upper half of the data.

The median of the lower half falls between two values.

$Q_{1} = \frac{25 + 27}{2} = 26$

The median of the upper half falls between two values.

$Q_{3} = \frac{43 + 45}{2} = 44$

The interquartile range is the difference between the third and first quartiles.

$Q_{3} - Q_{1} = 44 - 26 = 18$

Multiply by to find the answer:

Compare your answer with the correct one above

Question

Give the interquartile range of a data set with the following characteristics.

Mean: 72.1

Median: 70

Standard deviation: 4.6

Answer

The interquartile range is the difference between the first and third quartiles. The two pieces of information needed to determine interquartile range, the first and third quartiles, are missing; therefore, it is impossible to answer the question without more information.

Compare your answer with the correct one above

Question

Determine the interquartile range of the following numbers:

42, 51, 62, 47, 38, 50, 54, 43

Answer

How do you find the interquartile range?

We can find the interquartile range or IQR in four simple steps:

Order the data from least to greatest

Find the median

Calculate the median of both the lower and upper half of the data

The IQR is the difference between the upper and lower medians

Step 1: Order the data

In order to calculate the IQR, we need to begin by ordering the values of the data set from the least to the greatest. Likewise, in order to calculate the median, we need to arrange the numbers in ascending order (i.e. from the least to the greatest).

Let's sort an example data set with an odd number of values into ascending order.

$\textup{Odd data set}: 9, 3, 2, 5, 6, 11, 4, 3, 2$

$\textup{Odd data set (ascending)}: 2, 2, 3, 3, 4, 5, 6, 9, 11$

Now, let's perform this task with another example data set that is comprised of an even number of values.

$\textup{Even data set}: 11, 2, 4, 3, 8, 1, 2, 7, 4, 9$

Rearrange into ascending order.

$\textup{Even data set (ascending)}: 1, 2, 2, 3, 4, 4, 7, 8, 9, 11$

Step 2: Calculate the median

Next, we need to calculate the median. The median is the "center" of the data. If the data set has an odd number of data points, then the mean is the centermost number. On the other hand, if the data set has an even number of values, then we will need to take the arithmetic average of the two centermost values. We will calculate this average by adding the two numbers together and then dividing that number by two.

First, we will find the median of a set with an odd number of values. Cross out values until you find the centermost point

$\textup{Odd data set}: ot{2}, ot{2}, ot{3}, ot{3}, {\color{Red} 4}, ot{5}, ot{6}, ot{9}, ot{11}$

The median of the odd valued data set is four.

Now, let's find the mean of the data set with an even number of values. Cross out values until you find the two centermost points and then calculate the average the two values.

$\textup{Even data set}: ot{1}, ot{2}, ot{2}, ot{3}, {\color{Red} 4}, {\color{Red} 4}, ot{7}, ot{8}, ot{9}, ot{11}$

Find the average of the two centermost values.

$\textup{Average}=\frac{4+4}{2}$

$\textup{Average}=\frac{8}{2}$

$\textup{Average}=4$

The median of the even valued set is four.

Step 3: Upper and lower medians

Once we have found the median of the entire set, we can find the medians of the upper and lower portions of the data. If the data set has an odd number of values, we will omit the median or centermost value of the set. Afterwards, we will find the individual medians for the upper and lower portions of the data.

$\textup{Odd data set}: 2, 2, 3, 3, 4, 5, 6, 9, 11$

Omit the centermost value.

$\textup{Odd data set}: 2, 2, 3, 3,\mid 5, 6, 9, 11$

Find the median of the lower portion.

$\textup{Odd data set}: ot{2}, {\color{Red} 2}, {\color{Red} 3}, ot{3},\mid 5, 6, 9, 11$

Calculate the average of the two values.

$\textup{Average}=\frac{2+3}{2}$

$\textup{Average}=\frac{5}{2}$

$\textup{Average}=2.5$

The median of the lower portion is

Find the median of the upper portion.

$\textup{Odd data set}: 2, 2, 3, 3,\mid ot{5}, {\color{Red} 6}, {\color{Red} 9}, ot{11}$

Calculate the average of the two values.

$\textup{Average}=\frac{6+9}{2}$

$\textup{Average}=\frac{15}{2}$

$\textup{Average}=7.5$

The median of the upper potion is

If the data set has an even number of values, we will use the two values used to calculate the original median to divide the data set. These values are not omitted and become the largest value of the lower data set and the lowest values of the upper data set, respectively. Afterwards, we will calculate the medians of both the upper and lower portions.

$\textup{Even data set}: 1, 2, 2, 3, 4\mid 4, 7, 8, 9, 11$

Find the median of the lower portion.

$\textup{Even data set}: ot{1}, ot{2}, {\color{Red} 2}, ot{3}, ot{4}\mid 4, 7, 8, 9, 11$

The median of the lower portion is two.

Find the median of the upper portion.

$\textup{Even data set}: 1, 2, 2, 3, 4\mid ot{4}, ot{7}, {\color{Red} 8}, ot{9}, ot{11}$

The median of the upper portion is eight.

Step 4: Calculate the difference

Last, we need to calculate the difference of the upper and lower medians by subtracting the lower median from the upper median. This value equals the IQR.

Let's find the IQR of the odd data set.

$\textup{IQR of the odd data set}=7.5-2.5$

$\textup{IQR}=5$

Finally, we will find the IQR of the even data set.

$\textup{IQR of the even data set}=8-2$

$\textup{IQR}=6$

In order to better illustrate these values, their positions in a box plot have been labeled in the provided image.

Now that we have solved a few examples, let's use this knowledge to solve the given problem.

Solution:

First reorder the numbers in ascending order:

38, 42, 43, 47, 50, 51, 54, 62

Then divide the numbers into 2 groups, each containing an equal number of values:

(38, 42, 43, 47)(50, 51, 54, 62)

Q1 is the median of the group on the left, and Q3 is the median of the group on the right. Because there is an even number in each group, we'll need to find the average of the 2 middle numbers:

$Q1=\frac{42+43}{2}=\frac{85}{2}=42.5$

$Q3=\frac{51+54}{2}=\frac{105}{2}=52.5$

The interquartile range is the difference between Q3 and Q1:

Compare your answer with the correct one above

Question

Identify the first and third quartiles for the following set of numbers.

{11, 14, 9, 2, 27, 26, 5, 8, 19, 10, 12, 6}

Answer

{11, 14, 9, 2, 27, 26, 5, 8, 19, 10, 12, 6}

First, arrange the values in numerical order.

{2, 5, 6, 8, 9, 10, 11, 12, 14, 19, 26, 27}

Quartiles are the values that divide a set into four equal parts. Since this set has twelve values, "cut" the data after the 3rd and 9th value to find the 1st and 3rd quartile, respectively.

{2, 5, 6,| 8, 9, 10, 11, 12, 14,| 19, 26, 27}

The quartile will be the average of the values on either side of the "cut."

First Quartile = (6+8)/2=7

Third Quartile = (14+19)/2=16.5

Compare your answer with the correct one above

Question

Salespeople who land in the top quartile of average customer satisfaction ratings at the end of the year receive a bonus. Among the set of average ratings below, what is the cutoff for receiving the bonus?

{98, 55, 67, 88, 85, 91, 83, 65, 77, 83}

Answer

{98, 55, 67, 88, 85, 91, 83, 65, 77, 83}

Rearrange the values in order.

{55, 65, 67, 77, 83, 83, 85, 88, 91, 98}

To get quartiles, "cut" the data into four.

{55, 65, 6|7, 77, 83,| 83, 85, 8|8, 91, 98}

As you can see, the third "cut" is right at 88. Which means 88 is the cutoff for the top quartile based on this set of data.

Compare your answer with the correct one above

Tap the card to reveal the answer

Statistical Concepts - Algebra II

Number of Runs ScoredFrequency05122739435064728291 To determine the mean, first the data set should be re-written in sequential order: The formula to determine mean is: The mean is approximately 3.37 runs scored per game.

Adding up the total number of grandparents that were born outside the U.S. is our first step in solving this problem. There are people who said they had at least 1 grandparent born outside of the US. Of those, only 976 had exactly 3. So or is the answer.

Thousands of people in the United States were surveyed about their grandparents. This frequency table shows their answer to the question "how many of your grandparents were born outside of the US?" Is this data normally distributed?

What is the correct frequency distribution for this data set? 1 3 5 2 5 2 4 1 5 2 4 1 2 3 5 5 2 3 3 1 4 4 6 2 3 2 4

What is the mean of the data in this frequency table? # Frequency 1 3 2 4 3 0 4 2

The frequency table represents the data set: 1, 1, 1, 2, 2, 2, 2, 4, 4. The sum is 19 and there are 9 data points, so the mean is .

What is the median of the data in this frequency table? # Frequency 1 3 2 4 3 0 4 2

The frequency table represents the data set: 1, 1, 1, 2, 2, 2, 2, 4, 4. The median is 2 because 4 data points appear before and after the center 2.

Which frequency table has a median of 5? (The first column represents the data points, the second column the frequency)

Find the 85th percentile score in the following test results. {95, 88, 70, 75, 83, 70, 66, 91, 68, 76, 82}

Above is the stem-and-leaf display for a group of test scores. Which of the following scores would come closest to being at the percentile?

The stem-and-leaf display represents 53 scores. The score at the 35th percentile would be the score that is greater than 35% of the scores, or scores. Rounding, we count 19 scores from the bottom: The score represented is 64, which is the correct response.

Above is the stem-and-leaf display for a group of test scores. At what percentile would the student who made a score of 86 be?

If a student is ranked eight out of ten in a competition, what is the student's percentile rank?

The formula to calculate a percentile rank is: where represents total of scores below the rank, and is the total number of competitors. Substitute the values into the formula.

The times for a six-mile race are shown below. Sean: hours Ankur: hours Sarah: hours Fred: hours Ron: hours Jareth: hours Determine which percentile Sean's time is in.

In a litter of nine kittens, the only orange kitten weighs more than three in the litter, and less than the other remaining five. What is the percentile of the orange kitten's weight in comparison to the litter?

The percentile is equal to how many items in the set are equal to or less than the one in question divided by the total number of items in the set. Because there are four items equal to or less than the orange kitten's weight and there are nine items total in the set, the percentile is equal to or

98, 99, 99, 100, 101, 102, 104, 104, 105, 105, 107, 110, 112, 112 For the above data set, 102 is in what percentile?

In the data set, 102 is the 6th data point listed. There are 14 data points total. This means that % of the data is at or below 102. That's approximately the 43rd percentile.

98, 99, 99, 100, 101, 102, 104, 104, 105, 105, 107, 110, 112, 112 For the above data set, 110 is in what percentile?

The number 110 is the 12th in the list of 14 data points. That means that %. Since about 86% of the data points are at or below 110, it's in the 86th percentile.

Given the following set of data, what is twice the interquartile range?

How do you find the interquartile range?

Step 1: Order the data

Step 2: Calculate the median

Step 3: Upper and lower medians

Step 4: Calculate the difference

Solution:

Give the interquartile range of a data set with the following characteristics. Mean: 72.1 Median: 70 Standard deviation: 4.6

The interquartile range is the difference between the first and third quartiles. The two pieces of information needed to determine interquartile range, the first and third quartiles, are missing; therefore, it is impossible to answer the question without more information.

Determine the interquartile range of the following numbers: 42, 51, 62, 47, 38, 50, 54, 43

How do you find the interquartile range?

Step 1: Order the data

Step 2: Calculate the median

Step 3: Upper and lower medians

Step 4: Calculate the difference

Solution:

Identify the first and third quartiles for the following set of numbers. {11, 14, 9, 2, 27, 26, 5, 8, 19, 10, 12, 6}

Salespeople who land in the top quartile of average customer satisfaction ratings at the end of the year receive a bonus. Among the set of average ratings below, what is the cutoff for receiving the bonus? {98, 55, 67, 88, 85, 91, 83, 65, 77, 83}

Number of Runs Scored Frequency
0 5
1 2
2 7
3 9
4 3
5 0
6 4
7 2
8 2
9 1

To determine the mean, first the data set should be re-written in sequential order:

The formula to determine mean is:

$\bar{x}=\frac{\sum x}{n}=\frac{118}{35}\approx3.37$

The mean is approximately 3.37 runs scored per game.

Adding up the total number of grandparents that were born outside the U.S. is our first step in solving this problem.

There are

people who said they had at least 1 grandparent born outside of the US. Of those, only 976 had exactly 3.

So

$\frac{976}{15,631} = 0.062$ or is the answer.

Thousands of people in the United States were surveyed about their grandparents. This frequency table shows their answer to the question "how many of your grandparents were born outside of the US?"

Is this data normally distributed?

What is the correct frequency distribution for this data set?

1 3 5 2 5 2 4 1 5
2 4 1 2 3 5 5 2 3
3 1 4 4 6 2 3 2 4

What is the mean of the data in this frequency table?

# Frequency
1 3
2 4
3 0
4 2

The frequency table represents the data set:

1, 1, 1, 2, 2, 2, 2, 4, 4.

The sum is 19 and there are 9 data points, so the mean is

$\frac{19}{9} = 2.11$ .

What is the median of the data in this frequency table?

# Frequency
1 3
2 4
3 0
4 2

The frequency table represents the data set:

1, 1, 1, 2, 2, 2, 2, 4, 4.

The median is 2 because 4 data points appear before and after the center 2.

Find the 85th percentile score in the following test results.

{95, 88, 70, 75, 83, 70, 66, 91, 68, 76, 82}

Above is the stem-and-leaf display for a group of test scores. Which of the following scores would come closest to being at the $35^{th}$ percentile?

The stem-and-leaf display represents 53 scores. The score at the 35th percentile would be the score that is greater than 35% of the scores, or

$53 \times 0.35 \approx 18.5$ scores.

Rounding, we count 19 scores from the bottom:

The score represented is 64, which is the correct response.

The formula to calculate a percentile rank is: $\frac{x}{n}\cdot100$

where represents total of scores below the rank, and is the total number of competitors.

Substitute the values into the formula.

$\frac{2}{10}\cdot100 = 20$

The times for a six-mile race are shown below.

Sean: hours

Ankur: hours

Sarah: hours

Fred: hours

Ron: hours

Jareth: hours

Determine which percentile Sean's time is in.

In a litter of nine kittens, the only orange kitten weighs more than three in the litter, and less than the other remaining five.

What is the percentile of the orange kitten's weight in comparison to the litter?

98, 99, 99, 100, 101, 102, 104, 104, 105, 105, 107, 110, 112, 112

For the above data set, 102 is in what percentile?

In the data set, 102 is the 6th data point listed. There are 14 data points total. This means that $6 \div 14 \approx 0.4286 = 42.86$ % of the data is at or below 102. That's approximately the 43rd percentile.

98, 99, 99, 100, 101, 102, 104, 104, 105, 105, 107, 110, 112, 112

For the above data set, 110 is in what percentile?

The number 110 is the 12th in the list of 14 data points. That means that $12 \div 14 \approx 0.857 = 85.7$ %. Since about 86% of the data points are at or below 110, it's in the 86th percentile.

Give the interquartile range of a data set with the following characteristics.

Mean: 72.1

Median: 70

Standard deviation: 4.6

Determine the interquartile range of the following numbers:

42, 51, 62, 47, 38, 50, 54, 43

Identify the first and third quartiles for the following set of numbers.

{11, 14, 9, 2, 27, 26, 5, 8, 19, 10, 12, 6}

Salespeople who land in the top quartile of average customer satisfaction ratings at the end of the year receive a bonus. Among the set of average ratings below, what is the cutoff for receiving the bonus?

{98, 55, 67, 88, 85, 91, 83, 65, 77, 83}