Writing inequalities - Algebra 1
Card 0 of 20
Write an inequality that represents the following number line.
Write an inequality that represents the following number line.
On the number line, the graph starts at –1 and ends at 3.
The line runs between –1 and 3, so we know our inequality involves only values of x that fall between these two numbers. The open circle at –1 indicates that –1 is not included, while the shaded circle on 3 indicates that 3 is included.
Combining these two inequalities into one give us our answer.
On the number line, the graph starts at –1 and ends at 3.
The line runs between –1 and 3, so we know our inequality involves only values of x that fall between these two numbers. The open circle at –1 indicates that –1 is not included, while the shaded circle on 3 indicates that 3 is included.
Combining these two inequalities into one give us our answer.
Compare your answer with the correct one above
At a fair, there is a game where players step on a scale and weigh themselves. The objective of the game is for the host to guess the player's weight. A player loses if the host of the game can guess the player's weight within 
pounds, inclusive. Suppose a player weighs 
pounds. Write an inequality that represents the range of numbers such that the player loses. (Let 
represent the guess weight.)
At a fair, there is a game where players step on a scale and weigh themselves. The objective of the game is for the host to guess the player's weight. A player loses if the host of the game can guess the player's weight within
For the player to lose, the host has to guess within 
pounds of the player's weight, inclusive. Thus, the host can guess any number between 
pounds 
and 
pounds 
; that is, if 
is the weight the host guesses, then 
, which translates to 
.
For the player to lose, the host has to guess within
Compare your answer with the correct one above
Write a compound inequality that describes the given graph: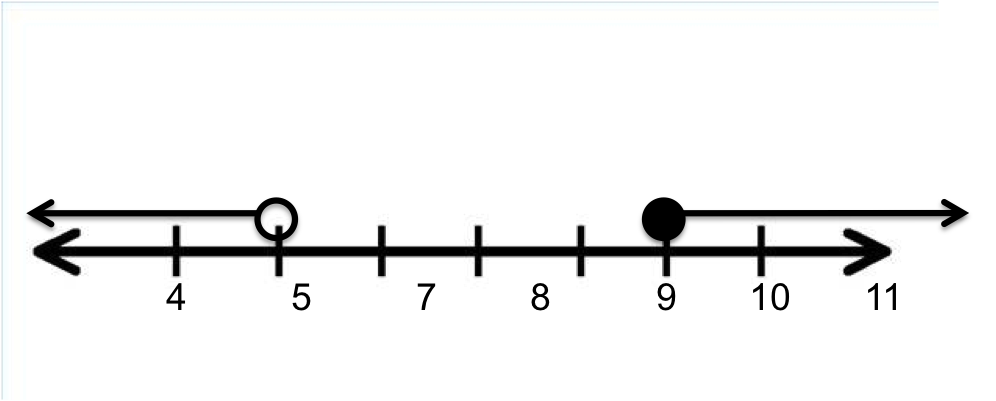
Write a compound inequality that describes the given graph:
The graph shows an arrow beginning on 5 with an open circle and pointing to the left, thus that portion of the graph says, all real numbers less than 5. There is a second arrow beginning on 9 with a closed circle and pointing to the right, representing all real numbers greater than or equal to 9. Since we are joining the two parts of the graph, we have a compound inequality utilizing the "or" statement. So our answer is 
.
The graph shows an arrow beginning on 5 with an open circle and pointing to the left, thus that portion of the graph says, all real numbers less than 5. There is a second arrow beginning on 9 with a closed circle and pointing to the right, representing all real numbers greater than or equal to 9. Since we are joining the two parts of the graph, we have a compound inequality utilizing the "or" statement. So our answer is
Compare your answer with the correct one above
Solve for 
:
Solve for
The first step is to distribute (multiply) through the parentheses:
Then subtract 
from both sides of the inequality:
Next, subtract the 12:
Finally, divide by two:
The first step is to distribute (multiply) through the parentheses:
Then subtract
Next, subtract the 12:
Finally, divide by two:
Compare your answer with the correct one above
A candy company is inspecting its factory. In a standard bag of candy there are a minimum of 14 individual candies, and a maximum of 22. Let 
be the number of candies in a standard bag. Write an expression for 
using inequalities.
A candy company is inspecting its factory. In a standard bag of candy there are a minimum of 14 individual candies, and a maximum of 22. Let
In terms of inequalities, we know two things. 
is greater than or equal to 14 (which is the same as 
being greater than 13). And we know 
is less than or equal to 22 (which is the same as 
being less than 23).
So, we have to find the correct statement where we can find the two inequalities. We see we need 
and 
.
Therefore the only answer that fits our needs is 
.
In terms of inequalities, we know two things.
So, we have to find the correct statement where we can find the two inequalities. We see we need
Therefore the only answer that fits our needs is
Compare your answer with the correct one above
Write as an algebraic inequality:
Twenty subtracted from the product of seven and a number exceeds one hundred.
Write as an algebraic inequality:
Twenty subtracted from the product of seven and a number exceeds one hundred.
"The product of seven and a number " is 
. "Twenty subtracted from the product of seven and a number" is 
. "Exceeds one hundred" means that this is greater than one hundred, so the correct inequality is
"The product of seven and a number " is
Compare your answer with the correct one above
Write as an algebraic inequality:
Twice the sum of a number and sixteen is no less than sixty.
Write as an algebraic inequality:
Twice the sum of a number and sixteen is no less than sixty.
"The sum of a number and sixteen" is translates to 
; twice that sum is 
. " Is no less than sixty" means that this is greater than or equal to sixty, so the desired inequality is
.
"The sum of a number and sixteen" is translates to
Compare your answer with the correct one above
Write as an algebraic inequality:
Twice the sum of a number and sixteen does not exceed eighty.
Write as an algebraic inequality:
Twice the sum of a number and sixteen does not exceed eighty.
"The sum of a number and sixteen" translates to 
; twice that sum is 
. "Does not exceed eighty" means that it is less than or equal to eighty, so the desired inequality is
"The sum of a number and sixteen" translates to
Compare your answer with the correct one above
Find the solution set of the inequality:
Find the solution set of the inequality:
or, in interval notation, 
or, in interval notation,
Compare your answer with the correct one above
Find the solution set of the inequality:
Find the solution set of the inequality:
or, in interval notation, 
or, in interval notation,
Compare your answer with the correct one above
Solve the inequality. 
Solve the inequality.
To solve 
, it is necessary to isolate the variable and the integers.
Subtract 
and 
from both sides of the equation.
Divide by nine on both sides.
This answer is also the same as: 
To solve
Subtract
Divide by nine on both sides.
This answer is also the same as:
Compare your answer with the correct one above
Choose the correct mathematical expression of the sentence,"A number 
is less than or equal to seventeen."
Choose the correct mathematical expression of the sentence,"A number
Choose the correct mathematical expression of the sentence,"A number 
is less than or equal to seventeen."
This sentence contains the phrase "less than or equal to." This means that we need to write an inequality. When writing inequalities, always remeber that the pointed end points to the smaller of the two values.
So, we have "A number 
..."
"...is less than or equal to..."
See how the inequality sign has the pointy end facing the 
? The pointy end should always face the smaller of the two values, and the open end should always face the larger of the two values. I was always taught that the inequality sign is like a hungry alligator. It always wants to eat the larger number!
Anyway,"...seventeen"
So we have our inequality. Note the horizontal line in the inequality sign. That is where we get the "...or equal to..." part.
Choose the correct mathematical expression of the sentence,"A number
This sentence contains the phrase "less than or equal to." This means that we need to write an inequality. When writing inequalities, always remeber that the pointed end points to the smaller of the two values.
So, we have "A number
"...is less than or equal to..."
See how the inequality sign has the pointy end facing the
Anyway,"...seventeen"
So we have our inequality. Note the horizontal line in the inequality sign. That is where we get the "...or equal to..." part.
Compare your answer with the correct one above
How would you write the equations: "I can spend no more than 
dollars when I go to the store today."
How would you write the equations: "I can spend no more than
The way the sentence is phrased suggests that the person can spend up to 
dollars but not a penny more. This suggests that 
, the amount spend can be 
but not exceed it.
So your answer is: 
The way the sentence is phrased suggests that the person can spend up to
So your answer is:
Compare your answer with the correct one above
Given the following problem, write the inequality.
Seven less than two times a number is greater than fourteen.
Given the following problem, write the inequality.
Seven less than two times a number is greater than fourteen.
Seven less than two times a number is greater than fourteen.
Let's look at the problem step by step.
If we do not know the value of a number, we give it a variable name. Let's say x. So, we see in the problem
Seven less than two times a number is greater than fourteen.
So, we will replace a number with x.
Seven less than two times x is greater than fourteen.
Now, we see that is says "two times" x, so we will write it like
Seven less than 2 x is greater than fourteen.
The problem says "seven less" than 2x. This simply means we are taking 2x and subtracting seven. So we get
2x - 7 is greater than fourteen
We know the symbol for "is greater than". We can write
2x - 7 > fourteen
Finally, we write out the number fourteen.
2x - 7 > 14
Seven less than two times a number is greater than fourteen.
Let's look at the problem step by step.
If we do not know the value of a number, we give it a variable name. Let's say x. So, we see in the problem
Seven less than two times a number is greater than fourteen.
So, we will replace a number with x.
Seven less than two times x is greater than fourteen.
Now, we see that is says "two times" x, so we will write it like
Seven less than 2 x is greater than fourteen.
The problem says "seven less" than 2x. This simply means we are taking 2x and subtracting seven. So we get
2x - 7 is greater than fourteen
We know the symbol for "is greater than". We can write
2x - 7 > fourteen
Finally, we write out the number fourteen.
2x - 7 > 14
Compare your answer with the correct one above
Express the following as an inequality:
Bob's amount of apples (
) is more than twice the amount of Adam's bananas (
).
Express the following as an inequality:
Bob's amount of apples (
To solve, you must convert the statement into an expression. The key work is "is". Whatever is on the left of that in the sentence will be on the left side of the expression. The same goes for the right. Thus, 
is on the left and 
is on the right.
To solve, you must convert the statement into an expression. The key work is "is". Whatever is on the left of that in the sentence will be on the left side of the expression. The same goes for the right. Thus,
Compare your answer with the correct one above
Write the following as a mathematical inequality:
A number is less than or equal to three times the sum of another number and five
Write the following as a mathematical inequality:
A number is less than or equal to three times the sum of another number and five
Write the following as a mathematical inequality:
A number is less than or equal to three times the sum of another number and five.
Let's begin with
"A number" let's call it x
"...is less than or equal to..."
So far we have:
Now,
"...three times..."
"...the sum of another number and five."
So, all together:
Write the following as a mathematical inequality:
A number is less than or equal to three times the sum of another number and five.
Let's begin with
"A number" let's call it x
"...is less than or equal to..."
So far we have:
Now,
"...three times..."
"...the sum of another number and five."
So, all together:
Compare your answer with the correct one above
Write an inequality for the following statement:
Two times the sum of 
and 
is greater than half of the product of 
and 
.
Write an inequality for the following statement:
Two times the sum of
When writing statments as inequalities, you must take it one step at a time. So in the statement
Two times the sum of 
and 
is greater than half of the product of 
and 
.
we will rewrite it one part at a time.
Two times the sum of 
and 
is greater than half of the product of 
and 
.
times the sum of 
and 
is greater than half of the product of 
and 
.
the sum of 
and 
is greater than half of the product of 
and 
.
is greater than half of the product of 
and 
.
half of the product of 
and 
.
of the product of 
and 
.
Simplify.
When writing statments as inequalities, you must take it one step at a time. So in the statement
Two times the sum of
we will rewrite it one part at a time.
Two times the sum of
Simplify.
Compare your answer with the correct one above
The admission for a carnival ride requires kids to be more than 40 inches tall, and no greater than 70 inches. Write the inequality.
The admission for a carnival ride requires kids to be more than 40 inches tall, and no greater than 70 inches. Write the inequality.
In order to write the inequality, we must find the key words in the sentence.
Write the equations from the following key words. Let 
be the height.
More than 40 inches tall: 
No greater than 70 inches: 
No greater than a certain height means it can be at that height, but cannot be greater than the given height.
The inequalities can be combined to a compound inequality:
The answer is: 
In order to write the inequality, we must find the key words in the sentence.
Write the equations from the following key words. Let
More than 40 inches tall:
No greater than 70 inches:
No greater than a certain height means it can be at that height, but cannot be greater than the given height.
The inequalities can be combined to a compound inequality:
The answer is:
Compare your answer with the correct one above
Write the inequality:
Two less than twice a number is less than two.
Write the inequality:
Two less than twice a number is less than two.
Break up the statement by parts. Let that number be 
.
Twice a number: 
Two less than twice a number: 
Less than two: 
Combine the parts.
The answer is: 
Break up the statement by parts. Let that number be
Twice a number:
Two less than twice a number:
Less than two:
Combine the parts.
The answer is:
Compare your answer with the correct one above
Write the inequality: Three less than twice a number is more than three times the number.
Write the inequality: Three less than twice a number is more than three times the number.
Break up the sentence into parts. Let the number be 
.
Twice a number: 
Three less than twice a number: 
Three less than twice a number is more than: 
Three times the number: 
Combine the terms to form the inequality.
The answer is: 
Break up the sentence into parts. Let the number be
Twice a number:
Three less than twice a number:
Three less than twice a number is more than:
Three times the number:
Combine the terms to form the inequality.
The answer is:
Compare your answer with the correct one above