How to write expressions and equations - Algebra 1
Card 0 of 20
(9_x_2 – 1) / (3_x_ – 1) =
(9_x_2 – 1) / (3_x_ – 1) =
It's much easier to use factoring and canceling than it is to use long division for this problem. 9_x_2 – 1 is a difference of squares. The difference of squares formula is a_2 – b_2 = (a + b)(a – b). So 9_x_2 – 1 = (3_x + 1)(3_x – 1). Putting the numerator and denominator together, (9_x_2 – 1) / (3_x_ – 1) = (3_x_ + 1)(3_x_ – 1) / (3_x_ – 1) = 3_x_ + 1.
It's much easier to use factoring and canceling than it is to use long division for this problem. 9_x_2 – 1 is a difference of squares. The difference of squares formula is a_2 – b_2 = (a + b)(a – b). So 9_x_2 – 1 = (3_x + 1)(3_x – 1). Putting the numerator and denominator together, (9_x_2 – 1) / (3_x_ – 1) = (3_x_ + 1)(3_x_ – 1) / (3_x_ – 1) = 3_x_ + 1.
Compare your answer with the correct one above
Simplify the following equation.
Simplify the following equation.
We can simplify the natural log exponents by using the following rules for naturla log.
Using these rules, we can perform the following steps.
Knowing that the e cancels the exponential natural log, we can cancel the first e.
Distribute the square into the parentheses and calculate.
Remember that a negative exponent is equivalent to a quotient. Write it as a quotient and then you're finished.
We can simplify the natural log exponents by using the following rules for naturla log.
Using these rules, we can perform the following steps.
Knowing that the e cancels the exponential natural log, we can cancel the first e.
Distribute the square into the parentheses and calculate.
Remember that a negative exponent is equivalent to a quotient. Write it as a quotient and then you're finished.
Compare your answer with the correct one above
Identify the real part of 
Identify the real part of
A complex number in its standard form is of the form: 
, where 
stands for the real part and 
stands for the imaginary part. The symbol 
stands for 
.
The real part in this problem is 1.
A complex number in its standard form is of the form:
The real part in this problem is 1.
Compare your answer with the correct one above
Divide: 
Answer must be in standard form.
Divide:
Answer must be in standard form.
Multiply both the numerator and the denominator by the conjugate of the denominator which is 
resulting in
This is equal to 
Since 
you can make that substitution of 
in place of 
in both numerator and denominator, leaving:
When you then cancel the negatives in both numerator and denominator (remember that 
, simplifying each term), you're left with a denominator of 
and a numerator of 
, which equals 
.
Multiply both the numerator and the denominator by the conjugate of the denominator which is
This is equal to
Since 
When you then cancel the negatives in both numerator and denominator (remember that 
Compare your answer with the correct one above
Compare your answer with the correct one above
Write in simplest form:
Write in simplest form:
Rewrite, then distribute:
Rewrite, then distribute:
Compare your answer with the correct one above
Translate this sentence into a mathematical equation:
Three less than five times a number is the same as two more than twice that number.
Translate this sentence into a mathematical equation:
Three less than five times a number is the same as two more than twice that number.
Three less than five times a number is the same as two more than twice that number.
Let the number be 
.
"Three less than five times a number" translates into 
.
"Is the same as" means equal to or "
".
"Two more than twice that number" means 
.
Putting these together gives:
Three less than five times a number is the same as two more than twice that number.
Let the number be
"Three less than five times a number" translates into
"Is the same as" means equal to or "
"Two more than twice that number" means
Putting these together gives:
Compare your answer with the correct one above
Rewrite the expression in simplest terms.
Rewrite the expression in simplest terms.
Here is the expression given: 
.
To simplify, follow the order of operations.
Distribute 
through the terms in the inner parentheses:
Now distribute 
into the terms of the remaining parentheses. Remember that 
multiplied by itself produces 
, but 
multiplied by 
produces 
:
Complete the multiplication to finish expanding:
Add like terms to reach the answer:
Here is the expression given:
To simplify, follow the order of operations.
Distribute
Now distribute
Complete the multiplication to finish expanding:
Add like terms to reach the answer:
Compare your answer with the correct one above
Rewrite the expression in simplest terms, where 
is the imaginary number 
.
Rewrite the expression in simplest terms, where
Writing this expression in simplest terms can be achieved by first factoring the radical into its smallest factors.
Multiplying the two 
together results in 
. Multiplying this by 
(which is simplified to 
) results in the answer 
.
Writing this expression in simplest terms can be achieved by first factoring the radical into its smallest factors.
Multiplying the two
Compare your answer with the correct one above
Rewrite the equation for 
in terms of 
.
Rewrite the equation for
The goal in expressing 
in terms of 
is to isolate 
on one side of the equation. One way to do this is to factor 
out of the fraction on the right side of the equation, then divide the entire equation by the fraction that remains after factoring. Remember that dividing by a fraction is the same as multiplying by the reciprocal of that fraction.
The left side of this equation will simply resolve into 
, although there are still 
variables on the right, so this is not yet in terms of 
. The right side resolves based on the rules for multiplying and dividing variables with exponents (add the exponents of like variables being multiplied, subtract the smaller exponent from the larger in the case of division, and change the variable to a 
if the resulting exponent is 
).
Since there is still a 
in the numerator on the right side of the equation, we will need to divide both sides of the equation by 
.
We have no solved for the reciprocal of 
in terms of 
. We simply flip both sides of the equation to get our answer.
The goal in expressing
The left side of this equation will simply resolve into
Since there is still a
We have no solved for the reciprocal of
Compare your answer with the correct one above
Mr. Wiggins does not have enough books for all the students in his algebra class. He has 20 students, 10 textbooks, and 16 workbooks. He wants to divide his students into work groups according to the following rules:
- Every student must work in a group of 2 (a pair) or 3 (a trio).
- Every Pair or Trio must have at least 1 textbook and at least 2 workbooks.
How many pairs and trios should Mr. Wiggins divide his students into if he wants to have as many pairs as possible while following these rules?
Mr. Wiggins does not have enough books for all the students in his algebra class. He has 20 students, 10 textbooks, and 16 workbooks. He wants to divide his students into work groups according to the following rules:
- Every student must work in a group of 2 (a pair) or 3 (a trio).
- Every Pair or Trio must have at least 1 textbook and at least 2 workbooks.
How many pairs and trios should Mr. Wiggins divide his students into if he wants to have as many pairs as possible while following these rules?
The conditions of Mr. Wiggins's problem can be expressed with an inequality and an equation to narrow down the number of pairs and trios that meets his conditions.
First, since each pair or trio must have at least 
workbooks, dividing the 
total workbooks into sets of 
means that there cannot be more than 
pairs and trios total. This can be expressed in the following inequality where 
is the number of pairs and 
is the number of trios.
Since each student must be in a pair or trio, we can set the number of total students (
) equal to the number of students in pairs (
) plus the number of students in trios (
).
To satisfy this inequality and this equation while maximizing 
(since Mr. Wiggins wants "as many pairs as possible"), start by substituting the maximum number of pairs (
) for 
, then work downward.
pairs would mean 
trios, according to the inequality 
. This does not satisfy the equation 
. Essentially, even though all of the workbooks are used, not all of the students have been accounted for. Continuing this pattern for 
, the sets 
, 
, 
, and 
satisfy the inequality, but they do NOT satisfy the equation.
satisfies the inequality and the equation, so the answer is 
pairs and 
trios.
The conditions of Mr. Wiggins's problem can be expressed with an inequality and an equation to narrow down the number of pairs and trios that meets his conditions.
First, since each pair or trio must have at least
Since each student must be in a pair or trio, we can set the number of total students (
To satisfy this inequality and this equation while maximizing
Compare your answer with the correct one above
Equations of a line can be represented as follows:
(1) 
(standard form)
(2) 
(slope-intercept form)
(3) 
(point-slope form)
Which of the following lines has 
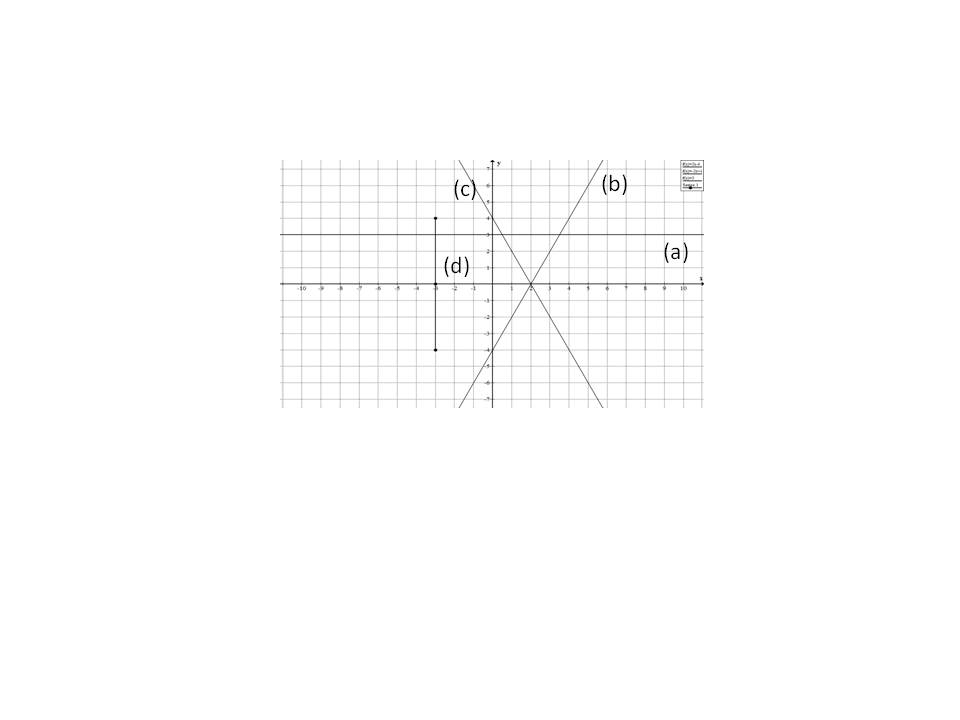
Equations of a line can be represented as follows:
(1)
(2)
(3)
Which of the following lines has
The equation of line 
is
Hence
and the
The equation of line
Hence
and the
Compare your answer with the correct one above
For the given equation determine the slope:
For the given equation determine the slope:
By changing the equation to slope intercept form we get the following:
Hence the slope is
By changing the equation to slope intercept form we get the following:
Hence the slope is
Compare your answer with the correct one above
What is the slope and the 
and 
intercepts of a line which passes through 
and 
?
What is the slope and the
For a vertical line e.g. 
, 
and 
This line does not intersect the 
and hence there is no 
.
Since the line passes through 
hence the 
-intercept 
.
For a vertical line e.g.
This line does not intersect the
Since the line passes through
Compare your answer with the correct one above
A car travels at a speed of 60 miles per hour. It is driven for 2.5 hours. How many miles does it travel?
A car travels at a speed of 60 miles per hour. It is driven for 2.5 hours. How many miles does it travel?
To solve this problem, you need to construct an algebraic equation. If 
is the distance traveled, then 
must equal to the speed multiplied by the time travelled. In this case, 
, which gives you a result of 150 miles.
To solve this problem, you need to construct an algebraic equation. If
Compare your answer with the correct one above
Write the equation of a line with a slope of
and passes through the point 
.
Write the equation of a line with a slope of
and passes through the point
Here we use the point-slope formula of a line which is
By plugging in 
, 
, and 
values we get the following:
which is equal to
When the above is simplified we get:
Here we use the point-slope formula of a line which is
By plugging in
which is equal to
When the above is simplified we get:
Compare your answer with the correct one above
Complete the missing information for the equation of the following line
and determine which one of the 
coordinates is not a solution to the above equation.
Complete the missing information for the equation of the following line
and determine which one of the
Replacing 
with 
, one gets 
which tells us that 
is not a solution.
Replacing
Compare your answer with the correct one above
Convert the following into the standard form of a line:
Convert the following into the standard form of a line:
Multiplying each term of the given equation by the denominator of the slope which is 5 one gets :
which can be written as
Multiplying each term of the given equation by the denominator of the slope which is 5 one gets :
which can be written as
Compare your answer with the correct one above
Find the equation of a line parallel to
and passes through 
.
Find the equation of a line parallel to
and passes through
The equation of a line parallel to the given line must be of the form:
Since the line passes through 
,
we can calculate 
by replacing 
with 2 and 
with 1 which gives us the following
Solving for 
gives us the following equation
The equation of a line parallel to the given line must be of the form:
Since the line passes through
we can calculate
Solving for
Compare your answer with the correct one above
Find the equation of a line perpendicular to
and passes through 
Find the equation of a line perpendicular to
and passes through
The slope of a line perpendicular to
which has a slope of 
, is the negative reciprocal of 
.
Hence we get
Replacing 
and 
with the given point we get
Solving for 
we get
The slope of a line perpendicular to
which has a slope of
Hence we get
Replacing
Solving for
Compare your answer with the correct one above