How to subtract trinomials - Algebra 1
Card 0 of 11
Solve this system of equations for  :
:


Solve this system of equations for 
Multiply the top equation by 3 on both sides, then add the second equation to eliminate the  terms:
terms:







Multiply the top equation by 3 on both sides, then add the second equation to eliminate the 
Compare your answer with the correct one above
Evaluate the following:

Evaluate the following:
To subtract these two trinomials, you first need to flip the sign on every term in the second trinomial, since it is being subtrated:


Next you can combine like terms. You have two terms with  , two terms with
, two terms with  , and two terms with no variable:
, and two terms with no variable:

To subtract these two trinomials, you first need to flip the sign on every term in the second trinomial, since it is being subtrated:
Next you can combine like terms. You have two terms with 

Compare your answer with the correct one above
Subtract:

Subtract:
When subtracting trinomials, first distribute the negative sign to the expression being subtracted, and then remove the parentheses: 
Next, identify and group the like terms in order to combine them:  .
.
When subtracting trinomials, first distribute the negative sign to the expression being subtracted, and then remove the parentheses:
Next, identify and group the like terms in order to combine them: 
Compare your answer with the correct one above
Simpify into quadratic form: 
Simpify into quadratic form:
First, FOIL the binomial combinations:
FOIL stands for the multiplication between the first terms, outer terms, inner terms, and then the last terms.

Next, distribute  into our new binomial and combine all compatible terms:
into our new binomial and combine all compatible terms:

So, our answer is  .
.
First, FOIL the binomial combinations:
FOIL stands for the multiplication between the first terms, outer terms, inner terms, and then the last terms.
Next, distribute 
So, our answer is 
Compare your answer with the correct one above
Simplify the following expression:

Simplify the following expression:
Let's solve this problem the long way, to see how it's done. Then we can look at a shortcut.
First, FOIL the binomial combinations:
FOIL stands for the multiplication between the first terms, outer terms, inner terms, and then the last terms.


Lastly, add the compatible terms in our trinomials:



So, our answer is  .
.
Now, let's look at a potentially faster way.
Look at our initial problem.

Notice how  can be found in both terms? Let's factor that out:
can be found in both terms? Let's factor that out:

Simpify the second term:

Now, perform a much easier multiplication:

So, our answer is  , and we had a much easier time getting there!
, and we had a much easier time getting there!
Let's solve this problem the long way, to see how it's done. Then we can look at a shortcut.
First, FOIL the binomial combinations:
FOIL stands for the multiplication between the first terms, outer terms, inner terms, and then the last terms.
Lastly, add the compatible terms in our trinomials:


So, our answer is 
Now, let's look at a potentially faster way.
Look at our initial problem.
Notice how 
Simpify the second term:
Now, perform a much easier multiplication:
So, our answer is 
Compare your answer with the correct one above
Simplify the following:

Simplify the following:

Now we add/subtract all like terms, yielding:

Now we add/subtract all like terms, yielding:
Compare your answer with the correct one above
Subtract  with
with  .
.
Subtract 

Group both trinomials with a parenthesis and set up the expression.

Simplify by removing the parentheses, distribute the negative sign, and rewrite the expression.

Combine like-terms.
The answer is: 
Group both trinomials with a parenthesis and set up the expression.
Simplify by removing the parentheses, distribute the negative sign, and rewrite the expression.
Combine like-terms.
The answer is:
Compare your answer with the correct one above
Simplify: 
Simplify:
To subtract polynomials, simply combine like terms. But be extremely careful to distribute the negative to ALL terms in the second polynomial! (Consider subtracting vertically to help.)
To subtract polynomials, simply combine like terms. But be extremely careful to distribute the negative to ALL terms in the second polynomial! (Consider subtracting vertically to help.)
Compare your answer with the correct one above
To subtract polynomials, simply combine like terms. But be extremely careful to distribute the negative to ALL terms in the second polynomial! (Consider subtracting vertically to help.)
To subtract polynomials, simply combine like terms. But be extremely careful to distribute the negative to ALL terms in the second polynomial! (Consider subtracting vertically to help.)
Compare your answer with the correct one above
Simplify: 
Simplify:
To subtract polynomials, simply combine like terms. But be extremely careful to distribute the negative to ALL terms in the second polynomial! (Consider subtracting vertically to help.)
Here, notice that the terms are not in the same order in both polynomials.
To subtract polynomials, simply combine like terms. But be extremely careful to distribute the negative to ALL terms in the second polynomial! (Consider subtracting vertically to help.)
Here, notice that the terms are not in the same order in both polynomials.
Compare your answer with the correct one above
Find the difference.
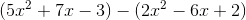
Find the difference.
When subtracting trinomials we distribute the negative sign and turn it into addition.

We then combine together coefficients of like terms.
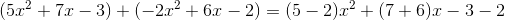

When subtracting trinomials we distribute the negative sign and turn it into addition.
We then combine together coefficients of like terms.
Compare your answer with the correct one above
