How to find the equation of a perpendicular line - Algebra 1

Card 0 of 20

Question

Find the equation of the line perpendicular to at the point .

Answer

The slope must be the negative reciprocal and the line must pass through the point (3,2). So the slope becomes and this is plugged into $2=-0.5\cdot 3+b$ to solve for the -intercept.

Compare your answer with the correct one above

Question

Which equation would give a line that is perpendicular to passes through ?

Answer

First, convert given equation to the slope-intercept form.

$y = \frac{-2}{3}x + 2$

In this format, we can tell that the slope is $m = \frac{-2}{3}$ . The slope of a perpendicular line will be the negative reciprocal, making $m_2 = \frac{3}{2}$ .

Next, substitute the slope into the slope-intercept form to get the intercept, using the point give in the question.

$5 = \frac{3}{2}(2)+ b$

The perpendicular equation becomes $y = \frac{3}{2}x +2$ . This equation can be re-written in the format of the asnwer chocies.

$y = \frac{3}{2}x +2$

$y-\frac{3}{2}x=2$

$2(y)-2(\frac{3}{2}x)=2(2)$

, or

Compare your answer with the correct one above

Question

Which line is perpendicular to $y=\frac{1}{2}x+10$ ?

Answer

Perpendicular lines have slopes that are negative inverses of each other. Since the original equation has a slope of $\frac{1}{2}$ , the perpendicular line must have a slope of . The only other equation with a slope of is .

Compare your answer with the correct one above

Question

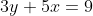
What is the slope of a line perpendicular to the line with the following equation?

$3y+5x=9$

Answer

Step 1: get the line into y = mx +b format to find the slope m:

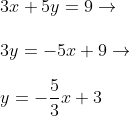
$\3x+5y=9\rightarrow \\ 3y=-5x+9\rightarrow\\ y=-\frac{5}{3}x+3$

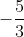Next, we need to remember that perpendicular lines have slopes that are negative reciprocals. Find the negative reciprocal of $-\frac{5}{3}$ :

$\frac{3}{5}$

Compare your answer with the correct one above

Question

Which of these lines is perpendicular to ?

Answer

Perpendicular lines have slopes that are negative reciprocals of one another. The slope of the given line is 9, so a line that is perpendicular to it must have a slope equivalent to its negative reciprocal, which is $-\frac{1}{9}$ .

Compare your answer with the correct one above

Question

Which of these lines is perpendicular to $y=\frac{1}{3}x+9$ ?

Answer

Perpendicular lines have slopes that are negative reciprocals of each other. The given line has a slope of $\frac{1}{3}$ . The negative reciprocal of $\frac{1}{3}$ is , so the perpendicular line must have a slope of . The only line with a slope of is .

Compare your answer with the correct one above

Question

Find the equation of the line that is perpendicular to and contains the point (5,3).

Answer

To find the equation of a line, we need to know the slope and a point that passes through the line. Once we know this, we can use the equation where m is the slope of the line, and $(x_{1},y_{1})$ is a point on the line. For perpendicular lines, the slopes are negative reciprocals of each other. The slope of is 5, so the slope of the perpendicular line will have a slope of $\frac{-1}{5}$ . We know that the perpendicular line needs to contain the point (5,3), so we have all of the information we need. We can now use the equation $y-y_1=m(x-x_1)\Rightarrow y-3=\frac{-1}{5}(x-5)\Rightarrow$ $y=\frac{-1}{5}x+1+3\Rightarrow y=\frac{-1}{5}x+4.$

Compare your answer with the correct one above

Question

Line runs through the following points:

: (2,3)

: (4,7)

Find the equation of Line , which is perpendicular to Line and runs through Point .

Answer

The equation of a line is written in the following format:

The first step, then, is to find the slope, .

is equal to the change in divided by the change in .

So,

$\frac{7-3}{4-2}=\frac{4}{2}=2$

The perpendicular slope of a line with a slope of 2 is the opposite reciprocal of 2, which is $-\frac{1}{2}$ .

Next step is to find . We don't need to find the equation of the original line; all we need from the original line is the slope. So all we need for is the perpendicular line. We can find values for and from the one point we have from the perpendicular line, plug them in, and solve for .

Our point is (4,7)

So,

$7=-\frac{1}{2}(4)+b$

Then we just fill in our value for , and we have as a function of .

$y=-\frac{1}{2}x+9$

Compare your answer with the correct one above

Question

$\textup{Find the }y\textup{-intercept of the line perpendicular to the segment between}\ \textup{points } (1,3) \textup{ and } (3,1) \textup{, and passing through its midpoint.}$

Answer

$\textup{The segment between points } (1,3) \textup{ and } (3,1) \textup{ has slope }\frac{1-3}{3-1}=-1.\\textup{ Therefore, any line perpendicular to it has slope the inverse reciprocal;}\\textup{that is, }-\frac{1}{-1}=1.$

$\textup{Of all the perpendicular lines }y=(1)x+p \textup{, the one passing through the}\\textup{midpoint }\left(\frac{1+3}{2},\frac{1+3}{2}\right)=(2,2) \textup{ is found by substituting } x=2\textup{ and } y=2\ \textup{ in the equation } y=x+p \textup{ and solving for } p \textup{, which gives the solution } p=0.$

Compare your answer with the correct one above

Question

Write the equation of a line perpendicular to $\small y=2x+1$ with a -intercept of .

Answer

This problem first relies on the knowledge of the slope-intercept form of a line, $\small y=mx+b$ , where m is the slope and b is the y-intercept.

In order for a line to be perpendicular to another line, its slope has to be the negative reciprocal. In this case, we are seeking a line to be perpendicular to $\small y=2x+1$ . This line has a slope of 2, a.k.a. $\small \frac{2}{1}$ . This means that the negative reciprocal slope will be $\small -\frac{1}{2}$ . We are told that the y-intercept of this new line is 4.

We can now put these two new pieces of information into $\small y=mx+b$ to get the equation

$\small y=-\frac{1}{2}x+4$ .

Compare your answer with the correct one above

Question

Write the equation of a line passing through the point $\small (-2, 3)$ that is perpendicular to the line $\small y=\frac{2}{3}x+5$ .

Answer

To solve this type of problem, we have to be familiar with the slope-intercept form of a line, $\small y=mx+b$ where m is the slope and b is the y-intercept. The line that our line is perpendicular to has the slope-intercept equation $\small y=\frac{2}{3}x+5$ , which means that the slope is $\small \frac{2}{3}$ .

The slope of a perpendicular line would be the negative reciprocal, so our slope is $\small -\frac{3}{2}$ .

We don't know the y-intercept of our line yet, so we can only write the equation as:

$\small y=- \frac{3}2x + b$ .

We do know that the point $\small (-2,3)$ is on this line, so to solve for b we can plug in -2 for x and 3 for y:

$\small 3 = -\frac{3}{2}-2+b$ First we can multiply $\small -\frac{3}{2}-2$ to get $\small 3$ .

This makes our equation now:

$\small 3 = 3 + b$ either by subtracting 3 from both sides, or just by looking at this critically, we can see that b = 0.

Our original $\small y=- \frac{3}2x + b$ becomes $\small \small y=- \frac{3}2x + 0$ , or simply $\small \small y=- \frac{3}2x$ .

Compare your answer with the correct one above

Question

Write the equation of a line perpendicular to

Answer

Two lines are perpendicular if and only if their slopes are "negative reciprocals" of each other such as 1/2 and -2. In our problem we are not given line equations that we can readily see the slope, so we must convert each equation to slope intercept form or .

First find out the slope of the given equation by converting it to slope-intercept form:

$y=-\frac{2}{16}x+4$

$y=-\frac{1}{8}x+4$

So we need a line whose slope is the negative reciprocal of -1/8 (which is 8). Even though this number is not "negative" the idea of the negative reicprocal gives a positive number here because two negative signs cancel each other to make a positive. $-\frac{1}{8}$ ...negative recicprocal... $-(-\frac{8}{1}=8)$ .

Now we must choose an equation that, after being changed to slope intercept form has a slope of 8.

$y=8x+\frac{7}{2}$

So (answer) is the equation of a line that is perpendicular to

.

Compare your answer with the correct one above

Question

What is a line that is perpendicular to ?

Answer

A line is perpendicular to another line when they meet at a degree angle. That angle is the result of the slopes of the lines being opposite reciprocals.

The "opposite reciprocal" of is best described as $-\frac{1}{m}$ .

First we reorganize the original equation to isolate . To do this we want to get our equation into slope intercept form .

First subtract 12 from each side.

Now divide by 4 and simplify where possible.

$y=3x-\frac{13}{4}$

opposite reciprocal $=-\frac{1}{m}=-\frac{1}{3}$

The only equation in the answer choices with a slope of $-\frac{1}{3}$ is

$y=-\frac{1}3x+4{}$ .

Compare your answer with the correct one above

Question

A line is perpendicular to and has a y-intercept of $\small \frac{27}{4}$ . Find the equation of this perpendicular line.

Answer

By definition, lines are perpendicular if the product of their slopes is $\small -1$ . For example, if a line has a slope of $\small 2$ , the perpendicular line would have a slope of $\small -\frac{1}{2}$ . This same concept can be used to solve this problem. Beginning with the issue of slope, we realize that the reference slope is $\small m=1$ . In order to create a product of $\small -1$ , we must multiply $\small +1$ by . Therefore, the slope of the perpendicular line is $\small -1$ .

Because the problem has not given us a point, we cannot use the point-slope formula to solve for the equation. However, we have been provided with the line's y-intercept. With this information, we are ready to construct the line's equation remembering the $\small y=mx+b$ skeleton. We have $\small m$ and now we have $\small b$ . Substituting in the given information will yield our answer.

$b=\frac{27}{4}$

$y={\color{Blue} -1}x+\frac{27}{4}$

Because $\small 1$ is usally not written in front of variables, we may omit it from the final answer.

Compare your answer with the correct one above

Question

A line perpendicular to $\small y=4x+1$ passes through the points $\small (0,0)$ and $\small (8,-2)$ . Find the equation of this line.

Answer

This problem can be quickly solved through using the point-slope formula considering the given information. Before we start substituting in values, however, it's important to remember what determines a line to be perpendicular relative to another. By definition, lines are perpendicular if their slopes have a product of $\small -1$ . For instance, if a line has a slope of $\small 2$ , the line perpendicular to it will have a slope of $\small -\frac{1}2$ because $\small 2 \cdot -\frac{1}{2}=-1$ . Using this concept, we must first determine the slope of the perpendicular line. We are given that the reference line has a slope of $\small 4$ . That means the perpendicular line must have a slope of $\small -\frac{1}{4}$ because $\small 4 \cdot -\frac{1}{4} = -1$ . Now that we know $\small m$ (slope) and have a coordinate, we have fulfilled the requirements of the point-slope formula and can begin to substitue in information and solve for the equation.

Here we arbitrarily use $\small (0,0)$

$y-0=-\frac{1}{4}(x-0)$

$y-0=-\frac{1}{4}x-0$

$y=-\frac{1}{4}x$

Compare your answer with the correct one above

Question

A line has a y-intercept of 7 and is perpendicular to a line with a slope of $\small -\frac{1}{2}$ . What is the equation of this perpendicular line?

Answer

Before beginning this problem, it's important to remember what defines a perpendicular line. A line is perpendicular to another if the product of the two lines' slope is $\small -1.$ For instance, if a line has a slope of $\small 2$ , the line perpendicular to it will have a slope of $\small -\frac{1}2$ because $\small 2 \cdot -\frac{1}{2}=-1$ . Using this concept, we must first determine the slope of the perpendicular line. The line of interest is perpendicular to a line with a slope of $\small -\frac{1}{2}$ , therefore its slope must be $\small m=2.$

The problem does not provide us enough information to use the point-slope formula to solve for the equation. However, we are provided with the line's y-intercept. This allows us to use the skeleton $\small y=mx+b$ to solve for the equation, where $\small m$ is slope and $\small b$ is the y-intercept.

$\small m=2$

$\small b=7$

$\small y={\color{Blue} 2}x+{\color{Blue} 7}$

Compare your answer with the correct one above

Question

Line 1 passes through points (0,2) and (3,3). Line 2 is perpindicular to Line 1. Also, Line 2 passes through the point (8,5). Which of the following represents the equation of Line 2?

Answer

Begin by calculating the slope of Line 1 as

$m_{1}=\frac{3-2}{3-0}=\frac{1}{3}$ .

Now, realize that since Line 2 is perpindicular to Line 1, the slope of Line 2 is the negative reciprocal of the slope of Line 1.

Therefore, the slope of Line 2 is given as

$m_{2}=-\frac{3}{1}=-3$ .

We also know that Line 2 passes through point (8,5).

Therefore, we may use "point-slope" form to express the equation of Line 2 as:

.

Finally, convert this "point-slope" equation to "slope-intercept" form in order to match the result with the correct answer choice:

.

Compare your answer with the correct one above

Question

Which of the following lines is perpendicular to the following line?

$y=\frac{1}{2}x+2$

Answer

Perpendicular lines have slopes that are opposite reciprocals meaning that the slope is flpped. The equation that satisfies both of these criteria is:

Compare your answer with the correct one above

Question

What is the equation of a line that is perpendicular to and passes through point ?

Answer

When finding the slope of a perpendicular line, we need to ensure we have form. stands for slope. Our is . To find the perpendicular slope, we need to take the negative reciprocal of that value which is $-\frac{1}{4}$ . Since we are looking for an equation, we need to reuse the form to solve for . We do this by plugging in our coordinates.

$2=-\frac{1}{4}*4+b$

Add on both sides.

Our equation is now $y=-\frac{1}{4}x+3$ .

Compare your answer with the correct one above

Question

What's the equation of a line that is perpendicular to and passes through point ?

Answer

When finding the slope of a perpendicular line, we need to ensure we have form. Let's rearrange it. By subtracting on both sides and dividing on both sides, we get $y=\frac{20-3x}{5}$ . stands for slope. Our is $-\frac{3}{5}$ . To find the perpendicular slope, we need to take the negative reciprocal of that value which is $\frac{5}{3}$ . Since we are looking for an equation, we need to reuse the form to solve for . We do this by plugging in our coordinates.

$1=\frac{5}{3}*9+b$

Subtract on both sides.

Our equation is now $y=\frac{5}{3}x-14$ .

Compare your answer with the correct one above

Tap the card to reveal the answer