How to graph a function - Advanced Geometry

Card 0 of 20

Question

Which of the following graphs does NOT represent a function?

Answer

This question relies on both the vertical-line test and the definition of a function. We need to use the vertical-line test to determine which of the graphs is not a function (i.e. the graph that has more than one output for a given input). The vertical-line test states that a graph represents a function when a vertical line can be drawn at every point in the graph and only intersect it at one point; thus, if a vertical line is drawn in a graph and it intersects that graph at more than one point, then the graph is not a function. The circle is the only answer choice that fails the vertical-line test, and so it is not a function.

Compare your answer with the correct one above

Question

Suppose .

To obtain the graph of , shift the graph a distance of units .

Answer

There are four shifts of the graph y = f(x):

y = f(x) + c shifts the graph c units upwards.

y = f(x) – c shifts the graph c units downwards.

y = f(x + c) shifts the graph c units to the left.

y = f(x – c) shifts the graph c units to the right.

Compare your answer with the correct one above

Question

The figure above shows the graph of y = f(x). Which of the following is the graph of y = |f(x)|?

Answer

One of the properties of taking an absolute value of a function is that the values are all made positive. The values themselves do not change; only their signs do. In this graph, none of the y-values are negative, so none of them would change. Thus the two graphs should be identical.

Compare your answer with the correct one above

Question

Below is the graph of the function :

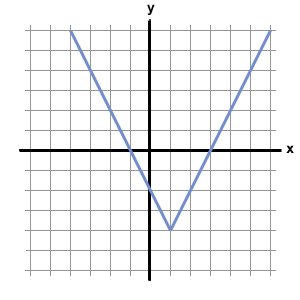
Which of the following could be the equation for ?

Answer

First, because the graph consists of pieces that are straight lines, the function must include an absolute value, whose functions usually have a distinctive "V" shape. Thus, we can eliminate f(x) = x2 – 4x + 3 from our choices. Furthermore, functions with x2 terms are curved parabolas, and do not have straight line segments. This means that f(x) = |x2 – 4x| – 3 is not the correct choice.

Next, let's examine f(x) = |2x – 6|. Because this function consists of an abolute value by itself, its graph will not have any negative values. An absolute value by itself will only yield non-negative numbers. Therefore, because the graph dips below the x-axis (which means f(x) has negative values), f(x) = |2x – 6| cannot be the correct answer.

Next, we can analyze f(x) = |x – 1| – 2. Let's allow x to equal 1 and see what value we would obtain from f(1).

f(1) = | 1 – 1 | – 2 = 0 – 2 = –2

However, the graph above shows that f(1) = –4. As a result, f(x) = |x – 1| – 2 cannot be the correct equation for the function.

By process of elimination, the answer must be f(x) = |2x – 2| – 4. We can verify this by plugging in several values of x into this equation. For example f(1) = |2 – 2| – 4 = –4, which corresponds to the point (1, –4) on the graph above. Likewise, if we plug 3 or –1 into the equation f(x) = |2x – 2| – 4, we obtain zero, meaning that the graph should cross the x-axis at 3 and –1. According to the graph above, this is exactly what happens.

The answer is f(x) = |2x – 2| – 4.

Compare your answer with the correct one above

Question

Which of the following could be a value of $f(x)$ for $f(x)=-x^2 + 3$ ?

Answer

The graph is a down-opening parabola with a maximum of $y=3$ . Therefore, there are no y values greater than this for this function.

Compare your answer with the correct one above

Question

What is the domain of $y = 4 - x^{2}$ ?

Answer

The domain of the function specifies the values that can take. Here, $4-x^{2}$ is defined for every value of , so the domain is all real numbers.

Compare your answer with the correct one above

Question

What is the domain of $y=-2\sqrt{x}$ ?

Answer

To find the domain, we need to decide which values can take. The is under a square root sign, so cannot be negative. can, however, be 0, because we can take the square root of zero. Therefore the domain is $x\geq 0$ .

Compare your answer with the correct one above

Question

What is the domain of the function $y=\sqrt{4-x^{2}}$ ?

Answer

To find the domain, we must find the interval on which $\sqrt{4-x^{2}}$ is defined. We know that the expression under the radical must be positive or 0, so $\sqrt{4-x^{2}}$ is defined when $x^{2}\leq 4$ . This occurs when $x \geq -2$ and $x \leq 2$ . In interval notation, the domain is $\left [ -2,2 \right ]$ .

Compare your answer with the correct one above

Question

Define the functions and as follows:

$\small \small f (x) = 2x + \sqrt{x - 1}$

$\small g (x) = 6x - \sqrt{x-1}$

What is the domain of the function ?

Answer

The domain of is the intersection of the domains of and . and are each restricted to all values of that allow the radicand to be nonnegative - that is,

$\small \small x - 1\geq 0$ , or

$\small \small \small x \geq 1$

Since the domains of and are the same, the domain of is also the same. In interval form the domain of is $\small \small [1, \infty )$

Compare your answer with the correct one above

Question

Define $f (x) = \frac{1}{x ^{2}- 25 }$ .

What is the natural domain of ?

Answer

The only restriction on the domain of is that the denominator cannot be 0. We set the denominator to 0 and solve for to find the excluded values:

$x ^{2}-25 =0$

$x ^{2}= 25$

$x = -5 \textrm{ or }x = 5$

The domain is the set of all real numbers except those two - that is,

$(-\infty , -5 ) \cup \left ( -5,5\right ) \cup (5, \infty)$ .

Compare your answer with the correct one above

Question

Define $g (x) = \frac{1}{\sqrt[3]{x -27}}$

What is the natural domain of ?

Answer

The radical in and of itself does not restrict the domain, since every real number has a real cube root. However, since the expression $\sqrt[3]{x -27}$ is in a denominator, it cannot be equal to zero, so the domain excludes the value(s) for which

$\sqrt[3]{x -27} = 0$

$\left (\sqrt[3]{x -27} \right )^{3}= 0^{3}$

27 is the only number excluded from the domain.

Compare your answer with the correct one above

Question

Define $g(x) = \frac{x}{x^{2}+3x-4 }$

What is the natural domain of ?

Answer

Since the expression $x^{2}+3x-4$ is in a denominator, it cannot be equal to zero, so the domain excludes the value(s) for which $x^{2}+3x-4 =0$ . We solve for by factoring the polynomial, which we can do as follows:

$x^{2}+3x-4 =0$

Replacing the question marks with integers whose product is and whose sum is 3:

$x + 4 = 0 \Rightarrow x = -4$

$x -1 = 0 \Rightarrow x = 1$

Therefore, the domain excludes these two values of .

Compare your answer with the correct one above

Question

What is the equation for the line pictured above?

Answer

A line has the equation

where is the intercept and is the slope.

The intercept can be found by noting the point where the line and the y-axis cross, in this case, at so .

The slope can be found by selecting two points, for example, the y-intercept and the next point over that crosses an even point, for example, .

Now applying the slope formula,

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

which yields $m=\frac{-1-2}{2-0}=-\frac{3}{2}$ .

Therefore the equation of the line becomes:

$y=-\frac{3}{2}x+2$

Compare your answer with the correct one above

Question

The chord of a $60^{\circ }$ central angle of a circle with circumference $90 \pi$ has what length?

Answer

A circle with circumference $90 \pi$ has as its radius

$90\pi \div 2\pi = 45$ .

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem, $\Delta AOB$ can be proved equilateral, so , the correct response.

Compare your answer with the correct one above

Question

The chord of a $60^{\circ }$ central angle of a circle with area $40 \pi$ has what length?

Answer

The radius of a circle with area $40 \pi$ can be found as follows:

$\pi r^{2} = A$

$\pi r^{2} = 40 \pi$

$r^{2} = 40$

$r = \sqrt{40 } = \sqrt{4} \cdot \sqrt{10} = 2 \sqrt{10}$

The circle, the central angle, and the chord are shown below:

By way of the Isosceles Triangle Theorem, $\Delta AOB$ can be proved equilateral, so $AB = AO= 2 \sqrt{10}$ , the correct response.

Compare your answer with the correct one above

Question

The chord of a $120^{\circ }$ central angle of a circle with area $32 \pi$ has what length?

Answer

The radius of a circle with area $32 \pi$ can be found as follows:

$\pi r^{2} = A$

$\pi r^{2} = 32 \pi$

$r^{2} = 32$

$r = \sqrt{32} = \sqrt{16} \cdot \sqrt{2} = 4 \sqrt{2}$

The circle, the central angle, and the chord are shown below, along with $\overline{AM}$ , which bisects isosceles $\Delta AOB$

We concentrate on $\Delta AOM$ , a 30-60-90 triangle. By the 30-60-90 Theorem,

$OM = \frac{1}{2}AO = \frac{1}{2} \cdot 4 \sqrt{2} = 2\sqrt{2}$

and

$AM = OM \sqrt{3} = 2 \sqrt{2} \cdot \sqrt{3} = 2 \sqrt{6}$

The chord $\overline{AB}$ has length twice this, or

$2 \cdot 2 \sqrt{6} = 4 \sqrt{6}$

Compare your answer with the correct one above

Question

Which of the following graphs represents the y-intercept of this function?

Answer

Graphically, the y-intercept is the point at which the graph touches the y-axis. Algebraically, it is the value of when .

Here, we are given the function . In order to calculate the y-intercept, set equal to zero and solve for .

So the y-intercept is at .

Compare your answer with the correct one above

Question

Which of the following graphs represents the x-intercept of this function?

Answer

Graphically, the x-intercept is the point at which the graph touches the x-axis. Algebraically, it is the value of for which .

Here, we are given the function . In order to calculate the x-intercept, set equal to zero and solve for .

So the x-intercept is at .

Compare your answer with the correct one above

Question

Which of the following represents $f(x)=\frac{1}{2}x-2$ ?

Answer

A line is defined by any two points on the line. It is frequently simplest to calculate two points by substituting zero for x and solving for y, and by substituting zero for y and solving for x.

$f(x)=\frac{1}{2}x-2$

Let . Then

$y=\frac{1}{2}(0)-2$

So our first set of points (which is also the y-intercept) is

Let . Then

$0=\frac{1}{2}x-2$

$2=\frac{1}{2}x$

So our second set of points (which is also the x-intercept) is .

Compare your answer with the correct one above

Question

Which graph accurately represents the following function:

Answer

The first step in determining which graph is correct is finding the origin of the function. If both x and y are equal to 0, the coordinates of the origin would be . The second step is to determine whether the graph opens up or down. The x and y are both positive, so the parabola will open upwards. The correct graph will look like

Compare your answer with the correct one above

Tap the card to reveal the answer