How to find the length of the diagonal of a rhombus - Advanced Geometry

Card 0 of 19

Question

Assume quadrilateral $\small EFGH$ is a rhombus. If the perimeter of $\small EFGH$ is $\small 24$ and the length of diagonal $\small \overline{EG}=10$ , what is the length of diagonal $\small \overline{FH}$ ?

Answer

To find the value of diagonal $\small \overline{FH}$ , we must first recognize some important properties of rhombuses. Since the perimeter is of $\small EFGH$ is $\small 24$ , and by definition a rhombus has four sides of equal length, each side length of the rhombus is equal to $\small 6$ . The diagonals of rhombuses also form four right triangles, with hypotenuses equal to the side length of the rhombus and legs equal to one-half the lengths of the diagonals. We can therefore use the Pythagorean Theorem to solve for one-half of the unknown diagonal:

$\small 6^2=5^2+x^2$ , where $\small 6$ is the rhombus side length, $\small 5$ is one-half of the known diagonal, and $\small x$ is one-half of the unknown diagonal. We can therefore solve for $\small x$ :

$\small x^2=6^2-5^2=36-25=11$

$\small x$ is therefore equal to $\small \sqrt{11}$ . Since $\small x$ represents one-half of the unknown diagonal, we need to multiply by $\small 2$ to find the full length of diagonal $\small \overline{FH}$ .

The length of diagonal $\small \overline{FH}$ is therefore $\small 2\sqrt{11}$

Compare your answer with the correct one above

Question

Assume quadrilateral $\small JKMN$ is a rhombus. If the area of $\small JKMN$ is $\small 273$ square units, and the length of diagonal $\small \overline{JM}$ is $\small 13$ units, what is the length of diagonal $\small \overline{KN}$ ?

Answer

This problem relies on the knowledge of the equation for the area of a rhombus, $\small \small A=\frac{pq}{2}$ , where $\small A$ is the area, and $\small p$ and $\small q$ are the lengths of the individual diagonals. We can substitute the values that we know into the equation to obtain:

$\small 273=\frac{(13)q}{2}$

$\small q=\frac{2 \cdot 273}{13}$

$\small q=42$

Therefore, our final answer is that the diagonal $\small \overline{KN}=42$

Compare your answer with the correct one above

Question

What is the second diagonal for the above rhombus?

Answer

Because a rhombus has vertical and horizontal symmetry, it can be broken into four congruent triangles, each with a hypotenuse of 13 and a base of 5 (half the given diagonal).

The Pythagorean Theorem

will yield,

$\sqrt{169-25}=12$ for the height of the triangles.

The greater diagonal is twice the height of the triangles therefore, the greater diagonal becomes:

$d=12 \cdot 2$

Compare your answer with the correct one above

Question

If the area of a rhombus is , and one of the diagonal lengths is , what is the length of the other diagonal?

Answer

The area of a rhombus is given below.

$A=\frac{d1\cdot d2}{2}$

Substitute the given area and a diagonal. Solve for the other diagonal.

$12=\frac{6\cdot d2}{2}$

$24=6\cdot d2$

Compare your answer with the correct one above

Question

If the area of a rhombus is , and a diagonal has a length of , what is the length of the other diagonal?

Answer

The area of a rhombus is given below. Plug in the area and the given diagonal. Solve for the other diagonal.

$A=\frac{d1 \cdot d2}{2}$

$2=\frac{1 \cdot d2}{2}$

Compare your answer with the correct one above

Question

The area of a rhombus is . The length of a diagonal is twice as long as the other diagonal. What is the length of the shorter diagonal?

Answer

Let the shorter diagonal be , and the longer diagonal be . The longer dimension is twice as long as the other diagonal. Write an expression for this.

$d2=2\cdot d1$

Write the area of the rhombus.

$A=\frac{d1 \cdot d2}{2}$

Since we are solving for the shorter diagonal, it's best to setup the equation in terms , so that we can solve for the shorter diagonal. Plug in the area and expression to solve for .

$5=\frac{d1 \cdot (2\cdot d1)}{2}$

$\sqrt5=d1$

Compare your answer with the correct one above

Question

If the area of a rhombus is , and the length of one of its diagonals is , what must be the length of the other diagonal?

Answer

Write the formula for the area of a rhombus.

$A=\frac{d_1\cdot d_2}{2}$

Plug in the given area and diagonal length. Solve for the other diagonal.

$60:cm^2=\frac{2:cm\cdot d_2}{2}$

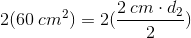
$2(60:cm^2)=2(\frac{2:cm\cdot d_2}{2})$

$120:cm^2=2:cm\cdot d_2$

$\frac{120:cm}{2:cm}=\frac{2:cm\cdot d_2}{2:cm}$

Compare your answer with the correct one above

Question

is a rhombus with side length . Diagonal $\overline{BD}$ has a length of . Find the length of diagonal $\overline{AC}$ .

Answer

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle to find the length of diagonal $\overline{AC}$ . From the problem, we are given that the sides are and $\overline{BD} = 12:cm$ . Because the diagonals bisect each other, we know:

$\overline{AD} = 10:cm$

$\overline{ED} = 6:cm$

Using the Pythagorean Theorem,

$(\overline{AE})^2 + (6:cm)^2 = (10:cm)^2$

$(\overline{AE})^2 + 36:cm^2 = 100:cm^2$

$(\overline{AE})^2 = 64:cm^2$

$\overline{AE} = 8:cm$

$\overline{AC} = 16:cm$

Compare your answer with the correct one above

Question

is a rhombus. $\overline{AB} = 17:cm$ $\overline{AB} = 17$ and $\overline{AC} = 30:cm$ . Find $\overline{BD}$ .

Answer

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle to find the length of diagonal $\overline{BD}$ . From the problem, we are given that the sides are and $\overline{AC} = 30:cm$ . Because the diagonals bisect each other, we know:

$\overline{AD} = 17:cm$

$\overline{AE} = 15:cm$

Using the Pythagorean Theorem,

$(\overline{ED})^2 + (15:cm)^2 = (17:cm)^2$

$(\overline{ED})^2 + 225:cm^2 = 289:cm^2$

$(\overline{ED})^2 = 64:cm^2$

$\overline{ED} = 8:cm$

$\overline{BD} = 16:cm$

Compare your answer with the correct one above

Question

is a rhombus. $\overline{BC} = 20$ and $\overline{BD} = 20$ . Find $\overline{AC}$ .

Answer

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle to find the length of diagonal $\overline{AC}$ . From the problem, we are given that the sides are and $\overline{BD} = 20$ . Because the diagonals bisect each other, we know:

$\overline{AD} = 20$

$\overline{ED} = 10$

Using the Pythagorean Theorem,

$\overline{AE}^2 + 10^2 = 20^2$

$\overline{AE}^2 = 300$

$\overline{AE} = 10\sqrt{3}$

$\overline{AC} = 20\sqrt{3}$

Compare your answer with the correct one above

Question

is a rhombus. $\overline{AB} = 4x + 9$ , $\overline{BD} = 2x + 6$ , and $\overline{AC} = 12x$ . Find .

Answer

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle and use the Pythagorean Theorem to solve for . From the problem:

$\overline{AD} = 4x + 9$

$\overline{BD} = 2x + 6$

$\overline{AC} = 12x$

Because the diagonals bisect each other, we know:

$\overline{ED} = x + 3$

$\overline{AE} = 6x$

Using the Pythagorean Theorem,

$\overline{AE}^2 + \overline{ED}^2 = \overline{AD}^2$

$\left ( 6x\right )^2 + \left ( x + 3\right )^2 = \left ( 4x + 9\right )^2$

Using the quadratic formula,

$x = \frac{b \pm \sqrt{b^2 - 4ac}}{2a}$

$x = \frac{66 \pm \sqrt{\left (-66 \right )^2 - 4\left (21 \right )\left (-72 \right )}}{2\left (21 \right )}$

With this equation, we get two solutions:

Only the positive solution is valid for this problem.

Compare your answer with the correct one above

Question

is a rhombus. $\overline{AB} = 3x - 2$ , $\overline{AC} = 4x + 4$ , and $\overline{BD} = 2x$ . Find .

Answer

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle and use the Pythagorean Theorem to solve for . From the problem:

$\overline{AD} = 3x-2$

$\overline{BD} = 2x$

$\overline{AC} = 4x + 4$

Because the diagonals bisect each other, we know:

$\overline{ED} = x$

$\overline{AE} = 2x + 2$

Using the Pythagorean Theorem,

$\overline{AE}^2 + \overline{ED}^2 = \overline{AD}^2$

$\left ( 2x + 2\right )^2 + \left ( x \right )^2 = \left ( 3x - 2\right )^2$

Factoring,

and

The first solution is nonsensical for this problem.

Compare your answer with the correct one above

Question

is rhombus with side lengths in meters. $\overline{AB} = 13$ and $\overline{BD} = 10$ . What is the length, in meters, of $\overline{AC}$ ?

Answer

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle to find the length of diagonal $\overline{AC}$ . From the given information, each of the sides of the rhombus measures meters and $\overline{BD} = 10$ .

Because the diagonals bisect each other, we know:

$\overline{AD} = 13$

$\overline{ED} = 5$

Using the Pythagorean theorem,

$\overline{AE}^2 + 5^2 = 13^2$

$\overline{AE}^2 = 144$

$\overline{AE} = 12$

$\overline{AC} = 24$

Compare your answer with the correct one above

Question

is a rhombus. $\overline{BD} = 18$ and $\overline{AC} = 80$ . Find the length of the sides.

Answer

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle to find the length of side $\overline{AD}$ . From the problem, we are given $\overline{BD} = 18$ and $\overline{AC} = 80$ . Because the diagonals bisect each other, we know:

$\overline{AE} = 40$

$\overline{ED} = 9$

Using the Pythagorean Theorem,

$40^2 + 9^2 = \overline{AD}^2$

$1681 = \overline{AD}^2$

$41 = \overline{AD}$

Compare your answer with the correct one above

Question

Rhombus has perimeter 48; $m \angle R = 60 ^{\circ }$ . What is the length of $\overline{RO}$ ?

Answer

The referenced rhombus, along with diagonals $\overline{RO}$ and $\overline{HM}$ , is below.

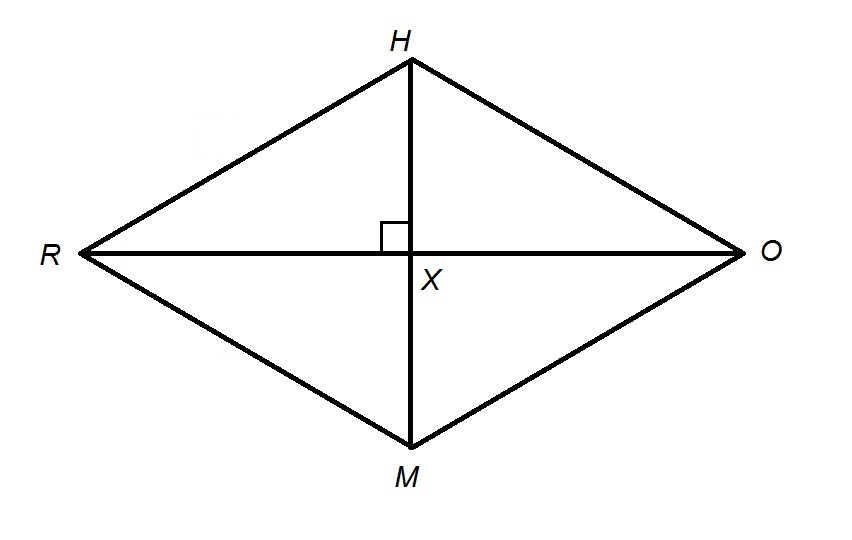
The four sides of a rhombus have equal measure, so each side has measure one fourth of the perimeter of 48, which is 12.

Since consecutive angles of a rhombus, as with any other parallelogram, are suplementary, $\angle RHO$ and $\angle RMO$ have measure $120^{\circ }$ ; the diagonals bisect $\angle MRH$ and $\angle RHO$ into $30 ^{\circ }$ and $60 ^{\circ }$ angles, respectively, to form four 30-60-90 triangles. $\bigtriangleup HXR$ is one of them; by the 30-60-90 Triangle Theorem, $HX = \frac{1}{2} \cdot RH = \frac{1}{2} \cdot 12 =6$ ,

and

$RX = HX \cdot \sqrt{3} = 6 \sqrt{3}$ .

Since the diagonals of a rhombus bisect each other, $RO = 2 \cdot RX = 2 \cdot 6 \sqrt{3} = 12\sqrt{3}$ .

Compare your answer with the correct one above

Question

Rhombus has perimeter 64; $m \angle R = 60 ^{\circ }$ . What is the length of $\overline{HM}$ ?

Answer

The sides of a rhombus are all congruent; since the perimeter of Rhombus is 64, each side measures one fourth of this, or 16.

The referenced rhombus, along with diagonal $\overline{HM}$ , is below:

Since consecutive angles of a rhombus, as with any other parallelogram, are supplementary, $\angle RHO$ and $\angle RMO$ have measure $120^{\circ }$ ; $\overline{HM}$ bisects both into $60 ^{\circ }$ angles, making $\bigtriangleup RHM$ equilangular and, as a consequence, equilateral. Therefore, .

Compare your answer with the correct one above

Question

Rhombus has area 56.

Which of the following could be true about the values of and ?

Answer

The area of a rhombus is half the product of the lengths of its diagonals, which here are $\overline{RO}$ and $\overline{HM}$ . This means

$\frac{1}{2} \cdot RO \cdot HM = 56$

Therefore, we need to test each of the choices to find the pair of diagonal lengths for which this holds.

:

Area: $\frac{1}{2} \cdot RO \cdot HM = \frac{1}{2} \cdot 28 \times 28 = 392$

Area: $\frac{1}{2} \cdot RO \cdot HM = \frac{1}{2} \cdot 14 \times 14 =98$

Area: $\frac{1}{2} \cdot RO \cdot HM = \frac{1}{2} \cdot 4 \times 14 = 28$

Area: $\frac{1}{2} \cdot RO \cdot HM = \frac{1}{2} \cdot16 \times 7 =56$

is the correct choice.

Compare your answer with the correct one above

Question

Find the lengths of the two diagonals, the longer diagonal is $d_{1}$ , the shorter diagonal is $d_{2}$ .

Answer

All sides of a rhombus are congruent.

Because all sides of a rhombus are congruent, the expressions of the side lengths can be set equal to each other. The resulting equation is then solved,

Because the sides of a rhombus are congruent, can be substituted into either or to find the length of a side,

, or, .

Each of the composing triangles are right triangles, so then is the length of the hypotenuse for each triangle.

.

The standard right triangle has a hypotenuse length equal to .

The hypotenuse of a standard right triangle is being multiplied by .

The result is , so then is the scale factor for the triangle side lengths.

For the standard right triangle, the other two side lengths are and $\sqrt{3}$ , so then the height of the triangle from step 7) has a height of , and the base length is $3(\sqrt{3})$ .

The base of the triangle from step 7) is

$\frac{1}{2}d_{1} = 3\cdot(\sqrt{3})$ ,

and the height is

$\frac{1}{2}d_{2} = 3(1)$ .

Diagonal

$d_2=2\cdot \frac{1}{2}d_{2} = 2\cdot3 = 6$ ,

and diagonal

$d_{1} = 2\cdot \frac{1}{2}d_{1} = 2\cdot3(\sqrt{3}) = 6(\sqrt{3})$ .

Compare your answer with the correct one above

Question

is a rhombus. Find $m(\overline{BD})$ .

Answer

Using the Law of Sines,

$\frac{sin(35^{o})}{6} = \frac{sin(110^{o})}{BD}$

$BD = \frac{6}{sin(35^{o})}\cdot sin(110^{o})$

$BD = m(\overline{BD})$

$m(\overline{BD})\approx 9.83$

Compare your answer with the correct one above

Tap the card to reveal the answer