How to find the length of the diagonal of a kite - Advanced Geometry

Card 0 of 20

Question

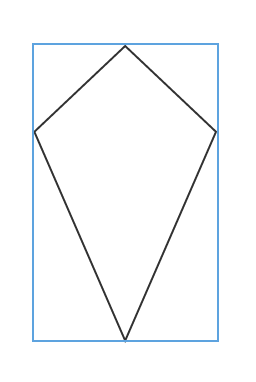
The area of the rectangle is , what is the area of the kite?

Answer

The area of a kite is half the product of the diagonals.

$A=\frac{p \cdot q}{2}$

The diagonals of the kite are the height and width of the rectangle it is superimposed in, and we know that because the area of a rectangle is base times height.

Therefore our equation becomes:

$A=\frac{l \cdot w}{2}$ .

We also know the area of the rectangle is $A=l \cdot w=80$ . Substituting this value in we get the following:

$A=\frac{l \cdot w}{2}=\frac{80}{2}=40$

Thus,, the area of the kite is .

Compare your answer with the correct one above

Question

Given: Quadrilateral such that $\overline{KI} \cong \overline{KE}$ , $\overline{TI} \cong \overline{TE}$ , $m \angle K = 60^{\circ }$ , $\angle T$ is a right angle, and diagonal $\overline{I E}$ has length 24.

Give the length of diagonal $\overline{KT}$ .

Answer

The Quadrilateral is shown below with its diagonals $\overline{I E}$ and $\overline{KT}$ .

. We call the point of intersection :

The diagonals of a quadrilateral with two pairs of adjacent congruent sides - a kite - are perpendicular; also, $\overline{KT}$ bisects the $60 ^{\circ }$ and $90^{\circ }$ angles of the kite. Consequently, $\bigtriangleup KXI$ is a 30-60-90 triangle and $\bigtriangleup TXI$ is a 45-45-90 triangle. Also, the diagonal that connects the common vertices of the pairs of adjacent sides bisects the other diagonal, making the midpoint of $\overline{IE}$ . Therefore,

$IX = \frac{1}{2} \cdot IE = \frac{1}{2} \cdot 24 = 12$ .

By the 30-60-90 Theorem, since $\overline{IX}$ and $\overline{KX}$ are the short and long legs of $\bigtriangleup KXI$ ,

$KX = IX \cdot \sqrt{3}= 12 \sqrt{3}$

By the 45-45-90 Theorem, since $\overline{IX}$ and $\overline{XT}$ are the legs of a 45-45-90 Theorem,

.

The diagonal $\overline{KT}$ has length

$KT =XT + KX= 12+ 12\sqrt{3}$ .

Compare your answer with the correct one above

Question

A kite has two perpendicular interior diagonals. One diagonal is twice the length of the other diagonal. The total area of the kite is $196\textup{ units}^{2}$ . Find the length of each interior diagonal.

Answer

To solve this problem, apply the formula for finding the area of a kite:

$Area=\frac{diagonalA\times diagonalB}{2}$

However, in this problem the question only provides information regarding the exact area. The lengths of the diagonals are represented as a ratio, where

Therefore, it is necessary to plug the provided information into the area formula. Diagonal is represented by and diagonal .

The solution is:

$196=\frac{x\times 2x}{2}$

$196\times2=x\times 2x$

$x^2=\frac{392}{2}=196$

$x=\sqrt{196}=14$

Thus, if , then diagonal must equal

Compare your answer with the correct one above

Question

A kite has two perpendicular interior diagonals. One diagonal has a measurement of and the area of the kite is $60\textup{ units}^{2}$ . Find the length of the other interior diagonal.

Answer

This problem can be solved by applying the area formula:

Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.

Thus the solution is:

$60=\frac{8\times diagonal B}{2}$

$60\times2=8\times diagonalB$

$diagonal B=\frac{120}{8}=15$

Compare your answer with the correct one above

Question

Using the kite shown above, find the length of the red (vertical) diagonal.

Answer

In order to solve this problem, first observe that the red diagonal line divides the kite into two triangles that each have side lengths of and Notice, the hypotenuse of the interior triangle is the red diagonal. Therefore, use the Pythagorean theorem: , where the length of the red diagonal.

The solution is:

$c=\sqrt{289}=\sqrt{17\times 17}=17$

Compare your answer with the correct one above

Question

A kite has two perpendicular interior diagonals. One diagonal has a measurement of and the area of the kite is $45\textup{ units}^{2}$ . Find the length of the other interior diagonal.

Answer

This problem can be solved by applying the area formula:

Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.

Thus the solution is:

$45=\frac{18\times diagonal B}{2}$

$45\times2=18\times diagonalB$

$diagonal B=\frac{90}{18}=5$

Compare your answer with the correct one above

Question

A kite has two perpendicular interior diagonals. One diagonal has a measurement of and the area of the kite is $6\textup{,}250\textup{ units}^{2}$ . Find the sum of the two perpendicular interior diagonals.

Answer

First find the length of the missing diagonal before you can find the sum of the two perpendicular diagonals.

To find the missing diagonal, apply the area formula:

This question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.

$6,250=\frac{250\times diagonal B}{2}$

$6250\times2=250\times diagonalB$

$diagonal B=\frac{12,500}{250}=50$

Therefore, the sum of the two diagonals is:

Compare your answer with the correct one above

Question

A kite has two perpendicular interior diagonals. One diagonal has a measurement of and the area of the kite is $28\textup{ units}^{2}$ . Find the sum of the two perpendicular interior diagonals.

Answer

You must find the length of the missing diagonal before you can find the sum of the two perpendicular diagonals.

To find the missing diagonal, apply the area formula:

This question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.

$28=\frac{4\times diagonal B}{2}$

$28\times2=4\times diagonalB$

$diagonal B=\frac{56}{4}=14$

Therefore, the sum of the two diagonals is:

Compare your answer with the correct one above

Question

The area of the kite shown above is $125\textup{ units}^{2}$ and the red diagonal has a length of . Find the length of the black (horizontal) diagonal.

Answer

To find the length of the black diagonal apply the area formula:

Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.

Thus the solution is:

$125=\frac{25\times diagonal B}{2}$

$125\times2=25\times diagonalB$

$diagonal B=\frac{250}{25}=10$

Compare your answer with the correct one above

Question

A kite has two perpendicular interior diagonals. One diagonal has a measurement of $22\textup{mm}$ and the area of the kite is $297\textup{mm}^{2}$ . Find the length of the other interior diagonal.

Answer

This problem can be solved by applying the area formula:

Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.

Thus the solution is:

$297=\frac{22\times diagonal B}{2}$

$297\times2=22\times diagonalB$

$diagonal B=\frac{594}{22}=27$

Compare your answer with the correct one above

Question

A kite has two perpendicular interior diagonals. One diagonal has a measurement of and the area of the kite is $1\textup{,}800\textup{ units}^{2}$ . Find the sum of the two perpendicular interior diagonals.

Answer

You must find the length of the missing diagonal before you can find the sum of the two perpendicular diagonals.

To find the missing diagonal, apply the area formula:

This question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.

$1800=\frac{40\times diagonal B}{2}$

$1800\times2=40\times diagonalB$

$diagonal B=\frac{3,600}{40}=90$

Therefore, the sum of the two diagonals is:

Compare your answer with the correct one above

Question

A kite has two perpendicular interior diagonals. One diagonal has a measurement of and the area of the kite is $54\textup{ units}^{2}$ . Find the length of the other interior diagonal.

Answer

This problem can be solved by applying the area formula:

Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.

Thus the solution is:

$54=\frac{9\times diagonal B}{2}$

$54\times2=9\times diagonalB$

$diagonal B=\frac{108}{9}=12$

Compare your answer with the correct one above

Question

A kite has two perpendicular interior diagonals. One diagonal has a measurement of and the area of the kite is $51\textup{ units}^{2}$ . Find the sum of the two perpendicular interior diagonals.

Answer

First find the length of the missing diagonal before you can find the sum of the two perpendicular diagonals.

To find the missing diagonal, apply the area formula:

This question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.

$51=\frac{17\times diagonal B}{2}$

$51\times2=17\times diagonalB$

$diagonal B=\frac{102}{17}=6$

Therefore, the sum of the two diagonals is:

Compare your answer with the correct one above

Question

A kite has two perpendicular interior diagonals. One diagonal has a measurement of $38\textup{cm}$ and the area of the kite is $855\textup{cm}^{2}$ . Find the length of the other interior diagonal.

Answer

This problem can be solved by applying the area formula:

Since this question provides the area of the kite and length of one diagonal, plug that information into the equation to solve for the missing diagonal.

Thus the solution is:

$855=\frac{38\times diagonal B}{2}$

$855\times2=38\times diagonalB$

$diagonal B=\frac{1,710}{38}=45$

Compare your answer with the correct one above

Question

If the length of the shorter diagonal is four, what is the length of the longer diagonal of this kite?

Answer

We can find the longer diagonal by adding together the altitude of the top triangle and the altitude of the bottom triangle. To find these, use Pythagorean Theorem. We can use Pythagorean Theorem because one of the properties of a kite is that the two diagonals are perpendicular.

The top triangle has two sides of length 3 \[labeled in the picture\], and a base of 4 \[provided in the written directions\]. To figure out the altitude, split this triangle into 2 right triangles. The two legs are x \[the altitude\] and 2 \[half of the base 4\], and the hypotenuse is 3:

subtract 4 from both sides

take the square root of both sides

$x=\sqrt5$

We will do something similar for the bottom triangle. Consider one of the right triangles. It will have a hypotenuse of 7, one leg that we don't know, x \[the altitude\], and one leg 2 \[half the shorter diagonal\]. Set up the equation using the Pythagorean Theorem:

subtract 4 from both sides

take the square root of both sides

$x = \sqrt{45}$

That can be simplified by considering 45 as the product of . Since the square root of 9 is 3, we can re-write $\sqrt{45}$ as $3\sqrt{5}$ .

Adding together the first answer of $\sqrt{5}$ plus $3\sqrt5$ gives $4\sqrt5$ .

Compare your answer with the correct one above

Question

Find the length of the diagonals of the kite.

Answer

The two diagonals are $\overline{AE}$ and $\overline{CD}$ .

To find $m(\overline{AE})$ , use the Law of Cosines and either $\angle C$ or $\angle D$ , because either angle is opposite $\overline{AE}$ .

Using $\angle C$ , $m(\angle C) = 70 + 40 = 110$ , and the Law of Cosines is

$(AE)^{2} = 7^{2} + 3^{2} - 2(7\cdot 3) \cdot cos(70 + 40)$

$= 49 + 9 - 2\cdot21\cdot cos(110)$

$= 58 - 42 \cdot cos(110)$

$\sqrt{(AE)^{2}} = \sqrt{58 - 42 \cdot cos(110)}$

$AE \approx 8.5$

To find $m(\overline{CD})$ , use the Law of Cosines using either $\angleA$ $\angle A$ or $\angle E$ , because either angle is opposite $\overline{CD}$ .

Using $\angle A$ , $m(\angle A) = 2 \cdot 20 = 40$ , and the Law of Cosines is

$(CD)^{2} = 7^{2} + 7^{2} - 2(7 \cdot 7) \cdot cos(20 + 20)$

$= 98 - 98 \cdot cos(40)$

$\sqrt{(CD)^{2}} = \sqrt{98 - 98 \cdot cos(40)}$

$CD \approx 4.79$

Compare your answer with the correct one above

Question

A kite has an area of square units, and one diagonal is units longer than the other. In unites, what is the length of the shorter diagonal?

Answer

Let be the length of the shorter diagonal. Then the length of the longer diagonal can be represented by .

Recall how to find the area of a kite:

$\text{Area}=\frac{(\text{Diagonal 1})(\text{Diagonal 2})}{2}$

Plug in the given area and solve for .

$119=\frac{x(x+3)}{2}$

Since we are dealing with geometric shapes, the answer must be a positive value. Thus, .

The length of the shorter diagonal is units long.

Compare your answer with the correct one above

Question

If the area of a kite is square units, and one diagonal is units longer than the other.

Answer

Let be the length of the shorter diagonal. Then the length of the longer diagonal can be represented by .

Recall how to find the area of a kite:

$\text{Area}=\frac{(\text{Diagonal 1})(\text{Diagonal 2})}{2}$

Plug in the given area and solve for .

$25=\frac{x(x+5)}{2}$

Since we are dealing with geometric shapes, the answer must be a positive value. Thus, .

The length of the shorter diagonal is units long.

Compare your answer with the correct one above

Question

If the area of a kite is square units, and one diagonal is units longer than the other, what is the length of the shorter diagonal?

Answer

Let be the length of the shorter diagonal. Then the length of the longer diagonal can be represented by .

Recall how to find the area of a kite:

$\text{Area}=\frac{(\text{Diagonal 1})(\text{Diagonal 2})}{2}$

Plug in the given area and solve for .

$198=\frac{x(x+4)}{2}$

Since we are dealing with geometric shapes, the answer must be a positive value. Thus, .

The length of the shorter diagonal is units long.

Compare your answer with the correct one above

Question

If the area of a kite is square units, and one diagonal is units longer than the other, what is the length of the longer diagonal?

Answer

Let be the length of the shorter diagonal. Then the length of the longer diagonal can be represented by .

Recall how to find the area of a kite:

$\text{Area}=\frac{(\text{Diagonal 1})(\text{Diagonal 2})}{2}$

Plug in the given area and solve for .

$20=\frac{x(x+3)}{2}$

Since we are dealing with geometric shapes, the answer must be a positive value. Thus, .

To find the longer diagonal, add .

The length of the longer diagonal is units long.

Compare your answer with the correct one above

Tap the card to reveal the answer