Transformation - Advanced Geometry
Card 0 of 20
Let f(x) = -2x2 + 3x - 5. If g(x) represents f(x) after it has been shifted to the left by three units, and then shifted down by four, which of the following is equal to g(x)?
Let f(x) = -2x2 + 3x - 5. If g(x) represents f(x) after it has been shifted to the left by three units, and then shifted down by four, which of the following is equal to g(x)?
We are told that g(x) is found by taking f(x) and shifting it to the left by three and then down by four. This means that we can represent g(x) as follows:
g(x) = f(x + 3) - 4
Remember that the function f(x + 3) represents f(x) after it has been shifted to the LEFT by three, whereas f(x - 3) represents f(x) after being shifted to the RIGHT by three.
f(x) = -2x2 + 3x - 5
g(x) = f(x + 3) - 4 = \[-2(x+3)2 + 3(x+3) - 5\] - 4
g(x) = -2(x2 + 6x + 9) + 3x + 9 - 5 - 4
g(x) = -2x2 -12x -18 + 3x + 9 - 5 - 4
g(x) = -2x2 - 9x - 18 + 9 - 5 - 4
g(x) = -2x2 - 9x - 18
The answer is -2x2 - 9x - 18.
We are told that g(x) is found by taking f(x) and shifting it to the left by three and then down by four. This means that we can represent g(x) as follows:
g(x) = f(x + 3) - 4
Remember that the function f(x + 3) represents f(x) after it has been shifted to the LEFT by three, whereas f(x - 3) represents f(x) after being shifted to the RIGHT by three.
f(x) = -2x2 + 3x - 5
g(x) = f(x + 3) - 4 = \[-2(x+3)2 + 3(x+3) - 5\] - 4
g(x) = -2(x2 + 6x + 9) + 3x + 9 - 5 - 4
g(x) = -2x2 -12x -18 + 3x + 9 - 5 - 4
g(x) = -2x2 - 9x - 18 + 9 - 5 - 4
g(x) = -2x2 - 9x - 18
The answer is -2x2 - 9x - 18.
Compare your answer with the correct one above
Regular pentagons have lines of symmetry through each vertex and the center of the opposite side, meaning the y-axis forms a line of symmetry in this instance. Therefore, point P is negative b units in the x-direction, and c units in the y-direction. It is a reflection of point (b,c) across the y-axis.

Regular pentagons have lines of symmetry through each vertex and the center of the opposite side, meaning the y-axis forms a line of symmetry in this instance. Therefore, point P is negative b units in the x-direction, and c units in the y-direction. It is a reflection of point (b,c) across the y-axis.
Compare your answer with the correct one above
Let f(x) = x3 – 2x2 + x +4. If g(x) is obtained by reflecting f(x) across the y-axis, then which of the following is equal to g(x)?
Let f(x) = x3 – 2x2 + x +4. If g(x) is obtained by reflecting f(x) across the y-axis, then which of the following is equal to g(x)?
In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding.

Therefore, g(x) = f(–x).
f(x) = x3 – 2x2 + x – 4
g(x) = f(–x) = (–x)3 – 2(–x)2 + (–x) + 4
g(x) = (–1)3x3 –2(–1)2x2 – x + 4
g(x) = –x3 –2x2 –x + 4.
The answer is –x3 –2x2 –x + 4.
In order to reflect a function across the y-axis, all of the x-coordinates of every point on that function must be multiplied by negative one. However, the y-values of each point on the function will not change. Thus, we can represent the reflection of f(x) across the y-axis as f(-x). The figure below shows a generic function (not f(x) given in the problem) that has been reflected across the y-axis, in order to offer a better visual understanding.

Therefore, g(x) = f(–x).
f(x) = x3 – 2x2 + x – 4
g(x) = f(–x) = (–x)3 – 2(–x)2 + (–x) + 4
g(x) = (–1)3x3 –2(–1)2x2 – x + 4
g(x) = –x3 –2x2 –x + 4.
The answer is –x3 –2x2 –x + 4.
Compare your answer with the correct one above
Line m passes through the points (–4, 3) and (2, –6). If line q is generated by reflecting m across the line y = x, then which of the following represents the equation of q?
Line m passes through the points (–4, 3) and (2, –6). If line q is generated by reflecting m across the line y = x, then which of the following represents the equation of q?
When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a).
Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2).
Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.
First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x1, y1) and (x2, y2).
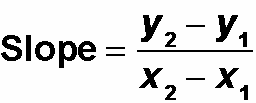
slope = (2 – (–4))/(–6 –3)
= 6/–9 = –2/3
Next, we can use the point-slope formula to find the equation for q.
y – y1 = slope(x – x1)
y – 2 = (–2/3)(x – (–6))
Multiply both sides by 3.
3(y – 2) = –2(x + 6)
3y – 6 = –2x – 12
Add 2x to both sides.
2x + 3y – 6 = –12
Add six to both sides.
2x + 3y = –6
The answer is 2x + 3y = –6.
When a point is reflected across the line y = x, the x and y coordinates are switched. In other words, the point (a, b) reflected across the line y = x would be (b, a).
Thus, if line m is reflected across the line y = x, the points that it passes through will be reflected across the line y = x. As a result, since m passes through (–4, 3) and (2, –6), when m is reflected across y = x, the points it will pass through become (3, –4) and (–6, 2).
Because line q is a reflection of line m across y = x, q must pass through the points (3, –4) and (–6, 2). We know two points on q, so if we determine the slope of q, we can then use the point-slope formula to find the equation of q.
First, let's find the slope between (3, –4) and (–6, 2) using the formula for slope between the points (x1, y1) and (x2, y2).
slope = (2 – (–4))/(–6 –3)
= 6/–9 = –2/3
Next, we can use the point-slope formula to find the equation for q.
y – y1 = slope(x – x1)
y – 2 = (–2/3)(x – (–6))
Multiply both sides by 3.
3(y – 2) = –2(x + 6)
3y – 6 = –2x – 12
Add 2x to both sides.
2x + 3y – 6 = –12
Add six to both sides.
2x + 3y = –6
The answer is 2x + 3y = –6.
Compare your answer with the correct one above
What is the period of the function?

What is the period of the function?

The period is the time it takes for the graph to complete one cycle.
In this particular case we have a sine curve that starts at 0 and completes one cycle when it reaches  .
.
Therefore, the period is 
The period is the time it takes for the graph to complete one cycle.
In this particular case we have a sine curve that starts at 0 and completes one cycle when it reaches 
Therefore, the period is
Compare your answer with the correct one above
If this is a sine graph, what is the phase displacement?
If this is a sine graph, what is the phase displacement?
The phase displacement is the shift from the center of the graph. Since this is a sine graph and the sin(0) = 0, this is in phase.
The phase displacement is the shift from the center of the graph. Since this is a sine graph and the sin(0) = 0, this is in phase.
Compare your answer with the correct one above
If this is a cosine graph, what is the phase displacement?
If this is a cosine graph, what is the phase displacement?
The phase displacement is the shift of the graph. Since cos(0) = 1, the phase shift is π because the graph is at its high point then.
The phase displacement is the shift of the graph. Since cos(0) = 1, the phase shift is π because the graph is at its high point then.
Compare your answer with the correct one above
If g(x) is a transformation of f(x) that moves the graph of f(x) four units up and three units left, what is g(x) in relation to f(x)?
If g(x) is a transformation of f(x) that moves the graph of f(x) four units up and three units left, what is g(x) in relation to f(x)?
To solve this question, you must have an understanding of standard transformations. To move a function along the x-axis in the positive direction, you must subtract the value from the operative x-value. For example, to move a function, f(x), five units to the left would be f(x+5).
To shift a function along the y-axis in the positive direction, you must add the value to the overall function. For example, to move a function, f(x), three units up would be f(x)+3.
The question asks us to move the function, f(x), left three units and up four units. f(x+3) will move the function three units to the left and f(x)+4 will move it four units up.
Together, this gives our final answer of f(x+3)+4.
To solve this question, you must have an understanding of standard transformations. To move a function along the x-axis in the positive direction, you must subtract the value from the operative x-value. For example, to move a function, f(x), five units to the left would be f(x+5).
To shift a function along the y-axis in the positive direction, you must add the value to the overall function. For example, to move a function, f(x), three units up would be f(x)+3.
The question asks us to move the function, f(x), left three units and up four units. f(x+3) will move the function three units to the left and f(x)+4 will move it four units up.
Together, this gives our final answer of f(x+3)+4.
Compare your answer with the correct one above
Let f(x) be a function. Which of the following represents f(x) after it has been reflected across the x-axis, then shifted to the left by four units, and then shifted down by five units?
Let f(x) be a function. Which of the following represents f(x) after it has been reflected across the x-axis, then shifted to the left by four units, and then shifted down by five units?
f(x) undergoes a series of three transformations. The first transformation is the reflection of f(x) across the x-axis. This kind of transformation takes all of the negative values and makes them positive, and all of the positive values and makes them negative. This can be represented by multiplying f(x) by –1. Thus, –f(x) represents f(x) after it is reflected across the x-axis.
Next, the function is shifted to the left by four. In general, if g(x) is a function, then g(x – h) represents a shift by h units. If h is positive, then the shift is to the right, and if h is negative, then the shift is to the left. In order, to shift the function to the left by four, we would need to let h = –4. Thus, after –f(x) is shifted to the left by four, we can write this as –f(x – (–4)) = –f(x + 4).
The final transformation requires shifting the function down by 5. In general, if g(x) is a function, then g(x) + h represents a shift upward if h is positive and a shift downward if h is negative. Thus, a downward shift of 5 to the function –f(x + 4) would be represented as –f(x + 4) – 5.
The three transformations of f(x) can be represented as –f(x + 4) – 5.
The answer is –f(x + 4) – 5.
f(x) undergoes a series of three transformations. The first transformation is the reflection of f(x) across the x-axis. This kind of transformation takes all of the negative values and makes them positive, and all of the positive values and makes them negative. This can be represented by multiplying f(x) by –1. Thus, –f(x) represents f(x) after it is reflected across the x-axis.
Next, the function is shifted to the left by four. In general, if g(x) is a function, then g(x – h) represents a shift by h units. If h is positive, then the shift is to the right, and if h is negative, then the shift is to the left. In order, to shift the function to the left by four, we would need to let h = –4. Thus, after –f(x) is shifted to the left by four, we can write this as –f(x – (–4)) = –f(x + 4).
The final transformation requires shifting the function down by 5. In general, if g(x) is a function, then g(x) + h represents a shift upward if h is positive and a shift downward if h is negative. Thus, a downward shift of 5 to the function –f(x + 4) would be represented as –f(x + 4) – 5.
The three transformations of f(x) can be represented as –f(x + 4) – 5.
The answer is –f(x + 4) – 5.
Compare your answer with the correct one above

The graphs of  and
and  are shown above. Which equation best describes the relationship between
are shown above. Which equation best describes the relationship between  and
and  ?
?
The graphs of 



Compare your answer with the correct one above
If the point (6, 7) is reflected over the line  and then over the x-axis, what is the resulting coordinate?
and then over the x-axis, what is the resulting coordinate?
If the point (6, 7) is reflected over the line 
A reflection over the line  involves a switching of the coordinates to get us (7, 6). A reflection over the x-axis involves a negation of the y-coordinate. Thus the resulting point is (7, –6).
involves a switching of the coordinates to get us (7, 6). A reflection over the x-axis involves a negation of the y-coordinate. Thus the resulting point is (7, –6).
A reflection over the line 
Compare your answer with the correct one above
You are looking at a map of your town and your house is located at the coordinate (0,0). Your school is located at the point (3,4). If each coordinate distance is 1.3 miles, how far away is your school?
You are looking at a map of your town and your house is located at the coordinate (0,0). Your school is located at the point (3,4). If each coordinate distance is 1.3 miles, how far away is your school?
The coordinate length between you and your school is equivalent to the hypotenuse of a right triangle with sides of 3 and 4 units:




The distance is 5 coordinate lengths, and each coordinate length corresponds to 1.3 miles of distance, so

The coordinate length between you and your school is equivalent to the hypotenuse of a right triangle with sides of 3 and 4 units:
The distance is 5 coordinate lengths, and each coordinate length corresponds to 1.3 miles of distance, so
Compare your answer with the correct one above
Let  . If
. If  is equal to
is equal to  when flipped across the x-axis, what is the equation for
when flipped across the x-axis, what is the equation for  ?
?
Let 



When a function  is flipped across the x-axis, the new function
is flipped across the x-axis, the new function  is equal to
is equal to  . Therefore, our function
. Therefore, our function  is equal to:
is equal to:

Our final answer is therefore 
When a function 



Our final answer is therefore
Compare your answer with the correct one above
Let  . If we let
. If we let  equal
equal  when it is flipped across the y-axis, what is the equation for
when it is flipped across the y-axis, what is the equation for  ?
?
Let 



When a function  is flipped across the y-axis, the resulting function
is flipped across the y-axis, the resulting function  is equal to
is equal to  . Therefore, to find our
. Therefore, to find our  , we must substitute in
, we must substitute in  for every
for every  is our equation:
is our equation:

Our final answer is therefore 
When a function 





Our final answer is therefore
Compare your answer with the correct one above
Let  . If
. If  represents
represents  is shifted
is shifted  places to the right and
places to the right and  places upwards, what is the equation for
places upwards, what is the equation for  ?
?
Let 





When a function  is transformed
is transformed  units upwards, the new function
units upwards, the new function  is equal to
is equal to  . Likewise, if
. Likewise, if  is transformed
is transformed  units to the right, the new function
units to the right, the new function  is equal to
is equal to  . Therfore, we can first find the upwards transformation by adding
. Therfore, we can first find the upwards transformation by adding  to the function:
to the function:

Now we can apply the horizontal transformation by replacing all  's in the function with
's in the function with  . Our transformed function therefore becomes:
. Our transformed function therefore becomes:

We then multiply this out to obtain:





Our final answer is therefore 
When a function 








Now we can apply the horizontal transformation by replacing all 

We then multiply this out to obtain:
Our final answer is therefore
Compare your answer with the correct one above
Assume we have a triangle,  , with the following vertices:
, with the following vertices:
 ,
,  , and
, and 
If  were reflected across the line
were reflected across the line  , what would be the coordinates of the new vertices?
, what would be the coordinates of the new vertices?
Assume we have a triangle, 


If 

When we reflect a point across the line,  , we swap the x- and y-coordinates; therefore, in each point, we will switch the x and y-coordinates:
, we swap the x- and y-coordinates; therefore, in each point, we will switch the x and y-coordinates:
 becomes
becomes  ,
,
 becomes
becomes  , and
, and
 becomes
becomes  .
.
The correct answer is the following:

The other answer choices are incorrect because we only use the negatives of the coordinate points if we are flipping across either the x- or y-axis.
When we reflect a point across the line, 






The correct answer is the following:
The other answer choices are incorrect because we only use the negatives of the coordinate points if we are flipping across either the x- or y-axis.
Compare your answer with the correct one above
How is  different from
different from  ?
?
How is 

The standard form of a linear equation is  Here, we are given two equations,
Here, we are given two equations,  and
and  , which differ only in their
, which differ only in their  terms. In other words, these functions differ only in their slope.
terms. In other words, these functions differ only in their slope.  has a larger slope than does
has a larger slope than does  , so
, so  is steeper.
is steeper.
The standard form of a linear equation is 






Compare your answer with the correct one above
Given  , write an equation
, write an equation  that represents a vertical shift four units upward.
that represents a vertical shift four units upward.
Given 

Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is  . Changes to the slope (
. Changes to the slope ( ) will make the graph steeper or shallower, changes to the y-intercept (
) will make the graph steeper or shallower, changes to the y-intercept ( ) will shift the graph vertically, and changes to the indepent variable (
) will shift the graph vertically, and changes to the indepent variable ( ) will shift the graph horizontally. Here, we are given
) will shift the graph horizontally. Here, we are given  and asked to transform it into a new equation vertically shifted up four units. We can accomplish this by adding four to the constant term, so the correct answer is
and asked to transform it into a new equation vertically shifted up four units. We can accomplish this by adding four to the constant term, so the correct answer is  .
.
 multiples the slope by four, which will result in a steeper graph.
multiples the slope by four, which will result in a steeper graph.
 subtracts four from the constant term, which shifts the graph vertically, but in the wrong direction.
subtracts four from the constant term, which shifts the graph vertically, but in the wrong direction.
 adds four to the independent variable, which shifts the graph horizontally to the left.
adds four to the independent variable, which shifts the graph horizontally to the left.
Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is 








Compare your answer with the correct one above
Given  , write an equation
, write an equation  that represents a horizontal shift two units to the right.
that represents a horizontal shift two units to the right.
Given 

Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is  . Changes to the slope (
. Changes to the slope ( ) will make the graph steeper or shallower, changes to the y-intercept (
) will make the graph steeper or shallower, changes to the y-intercept ( ) will shift the graph vertically, and changes to the indepent variable (
) will shift the graph vertically, and changes to the indepent variable ( ) will shift the graph horizontally. Here, we are given
) will shift the graph horizontally. Here, we are given  and asked to transform it into a new equation horizontally shifted to the right two units. We can accomplish this by subtracting two from the independent variable, so the correct answer is
and asked to transform it into a new equation horizontally shifted to the right two units. We can accomplish this by subtracting two from the independent variable, so the correct answer is  .
.
 adds two to the constant term, which shifts the graph vertically.
adds two to the constant term, which shifts the graph vertically.
 adds two to the independent variable which shifts the graph horizontally, but in the wrong direction.
adds two to the independent variable which shifts the graph horizontally, but in the wrong direction.
 multiplies the slope by two, which makes the graph steeper.
multiplies the slope by two, which makes the graph steeper.
Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is 








Compare your answer with the correct one above
Given  , write an equation
, write an equation  that increases the slope by three, shifts the graph horizontally one unit to the left, and shifts the graph vertically three units down.
that increases the slope by three, shifts the graph horizontally one unit to the left, and shifts the graph vertically three units down.
Given 

Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is  . Changes to the slope (
. Changes to the slope ( ) will make the graph steeper or shallower, changes to the y-intercept (
) will make the graph steeper or shallower, changes to the y-intercept ( ) will shift the graph vertically, and changes to the indepent variable (
) will shift the graph vertically, and changes to the indepent variable ( ) will shift the graph horizontally. Here, we are given
) will shift the graph horizontally. Here, we are given  and asked to transform it into a new equation that increases the slope by three, shifts the graph horizontally one unit to the left, and shifts the graph vertically three units down.
and asked to transform it into a new equation that increases the slope by three, shifts the graph horizontally one unit to the left, and shifts the graph vertically three units down.
First, multiply the slope by three.

Add one to the independent variable.

Subtract three from the constant term.

 correctly increases the slope and subtracts three from the constant term, but fails to properly substitute
correctly increases the slope and subtracts three from the constant term, but fails to properly substitute  for
for  , leading to an erroneous simplification. In other words,
, leading to an erroneous simplification. In other words,  becomes
becomes  .
.
 shifts the function to the right instead of the left.
shifts the function to the right instead of the left.
 shifts the function both right and up, rather than left and down.
shifts the function both right and up, rather than left and down.
Algebraic transformations of functions rely on manipulating components of the equation's standard form. The standard form of a linear equation is 




First, multiply the slope by three.
Add one to the independent variable.
Subtract three from the constant term.







Compare your answer with the correct one above




