How to find research summary in chemistry - ACT Science
Card 0 of 20
Chemists can model how solids, liquids, and gases behave at different temperatures and pressures with a graph called a phase diagram. When the pressure and temperature are simultaneously known, a scientist can predict whether the material will be in a specific state. The diagram is divided into sections depending on the phase and the lines between sections represent phase transitions occurring between two or more separate phases.
In general, solids of neatly stacked molecules exist when temperatures are low and pressures are intermediate. These values decrease the kinetic energy of the molecules enough to allow for attractive forces to begin the stacking process. Liquids, by contrast, are found at intermediate pressures and temperatures. The temperature is high enough to impart enough kinetic energy to prevent solid formation and the pressure is high enough to prevent the liquid from becoming a gas. Finally, a gas forms at low pressures and high temperatures. The high level of kinetic energy prevents molecules from associating with one another.
Materials can undergo processes called phase transitions, meaning they can transition from one phase to another. The transition from a solid to a liquid is called melting, while the reverse transition is called freezing. Vaporization occurs when a liquid becomes a gas, while condensation occurs when a gas becomes a liquid. Finally, in a process called sublimation, a solid can directly become a gas without passing through a liquid phase. Additionally, when a gas directly becomes a solid, this is known as deposition.
In order to predict the state of a material, the scientist must know __________.
Chemists can model how solids, liquids, and gases behave at different temperatures and pressures with a graph called a phase diagram. When the pressure and temperature are simultaneously known, a scientist can predict whether the material will be in a specific state. The diagram is divided into sections depending on the phase and the lines between sections represent phase transitions occurring between two or more separate phases.
In general, solids of neatly stacked molecules exist when temperatures are low and pressures are intermediate. These values decrease the kinetic energy of the molecules enough to allow for attractive forces to begin the stacking process. Liquids, by contrast, are found at intermediate pressures and temperatures. The temperature is high enough to impart enough kinetic energy to prevent solid formation and the pressure is high enough to prevent the liquid from becoming a gas. Finally, a gas forms at low pressures and high temperatures. The high level of kinetic energy prevents molecules from associating with one another.
Materials can undergo processes called phase transitions, meaning they can transition from one phase to another. The transition from a solid to a liquid is called melting, while the reverse transition is called freezing. Vaporization occurs when a liquid becomes a gas, while condensation occurs when a gas becomes a liquid. Finally, in a process called sublimation, a solid can directly become a gas without passing through a liquid phase. Additionally, when a gas directly becomes a solid, this is known as deposition.
In order to predict the state of a material, the scientist must know __________.
The passage states that a scientist must know both temperature and pressure in order to find where in the phase diagram a material is. Without this knowledge, the scientist cannot determine whether the material is in a solid, liquid, or gaseous state.
The passage states that a scientist must know both temperature and pressure in order to find where in the phase diagram a material is. Without this knowledge, the scientist cannot determine whether the material is in a solid, liquid, or gaseous state.
Compare your answer with the correct one above
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
In an oxygen molecule, O2, the two oxygen atoms oscillate about a fixed central point. Which form of kinetic energy is best described here?
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
In an oxygen molecule, O2, the two oxygen atoms oscillate about a fixed central point. Which form of kinetic energy is best described here?
In the first paragraph, the passage tells us that individual atoms in a bond that move towards and away from each other constitute vibrational energy. Based on the question, the two oxygen atoms oscillate around the central point (the mid-point of their bond). Thus, this is vibrational energy.
In the first paragraph, the passage tells us that individual atoms in a bond that move towards and away from each other constitute vibrational energy. Based on the question, the two oxygen atoms oscillate around the central point (the mid-point of their bond). Thus, this is vibrational energy.
Compare your answer with the correct one above
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
An oxygen molecule moving from the left side of a chamber to the right would display what type(s) of kinetic energy?
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
An oxygen molecule moving from the left side of a chamber to the right would display what type(s) of kinetic energy?
In the first passage, after describing the different types of kinetic energy, the passage notes that a molecule would likely have varying combinations of kinetic energy. Thus, a molecule moving across the room would display translational, vibrational, and rotational motion.
In the first passage, after describing the different types of kinetic energy, the passage notes that a molecule would likely have varying combinations of kinetic energy. Thus, a molecule moving across the room would display translational, vibrational, and rotational motion.
Compare your answer with the correct one above
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
The relationship between total energy, kinetic energy, and potential energy could best be described as:
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
The relationship between total energy, kinetic energy, and potential energy could best be described as:
The end of the first paragraph helps us answer this question. We are told that a molecule contains a fixed amount of total energy and that some combination of kinetic and potential energy combines to create this sum total. Thus, the relationship that best depicts how the various forms of energy relate is 
.
The end of the first paragraph helps us answer this question. We are told that a molecule contains a fixed amount of total energy and that some combination of kinetic and potential energy combines to create this sum total. Thus, the relationship that best depicts how the various forms of energy relate is
Compare your answer with the correct one above
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
As the kinetic energy of a molecule increases, one would expect the potential energy to:
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
As the kinetic energy of a molecule increases, one would expect the potential energy to:
Using the last few sentences of the first paragraph as a guide, we can see that the total energy is fixed. Thus, some combination of kinetic and potential energies makes up the total energy. We can relate how the energies combine with the following formula: 
. Thus, if the kinetic energy increases, the potential energy would have to decrease to keep the sum total the same.
Using the last few sentences of the first paragraph as a guide, we can see that the total energy is fixed. Thus, some combination of kinetic and potential energies makes up the total energy. We can relate how the energies combine with the following formula:
Compare your answer with the correct one above
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
As the potential energy of a molecule decreases, one would expect the kinetic energy to:
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
As the potential energy of a molecule decreases, one would expect the kinetic energy to:
Using the last few sentences of the first paragraph as a guide, we can see that the total energy of a molecule is fixed and contains a fixed combination of kinetic and potential energies. Thus, we can relate the combination to the total by the following formula: 
. Thus, if the potential energy decreases, the kinetic energy must increase in order to keep the total energy of the molecule constant.
Using the last few sentences of the first paragraph as a guide, we can see that the total energy of a molecule is fixed and contains a fixed combination of kinetic and potential energies. Thus, we can relate the combination to the total by the following formula:
Compare your answer with the correct one above
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
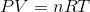
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
The relationship between kinetic and potential energy may best be illustrated by:
Both gases and liquids are considered to be fluids that have individual molecules that move around with kinetic and potential energy. Kinetic energy, defined as the energy related to motion, takes three forms: translational energy that occurs as a molecule moves from position A to position B, rotational energy that occurs as a molecule spins around an imaginary axis at its center of mass, and vibrational energy that occurs as individual atoms in a molecular bond move towards and away from each other. Usually, molecules possess varying combinations of kinetic energy forms. In contrast, potential energy is defined as stored energy that could be released to become kinetic energy. The total energy of a molecule is fixed, meaning that a molecule has some combination of kinetic and potential energies.
Varying amount of kinetic and potential energies define how molecules in a fluid interact with each other. For example, when the kinetic energy of a molecule is high (greater than 1000J), it can no longer interact with neighboring molecules strongly enough to remain a liquid. However, if the potential energies are too high (greater than 1000 J), molecules cannot escape a liquid to become a gas. If the kinetic energy is high and the potential energy is low, molecules tend to become a gas and can be modeled by an equation known as the Ideal Gas Law:
Where P is the pressure of a gas, V is the volume, n is the number of moles of a gas, R is a constant, and T is temperature in degrees Kelvin.
The Ideal Gas Law perfectly applies to particles with no mass, no intermolecular interactions, and no true volume. However, real molecules do not adhere perfectly to the Ideal Gas Law.
The relationship between kinetic and potential energy may best be illustrated by:
The first paragraph helps us understand that a total amount of energy is fixed per molecule and is a combination of kinetic and potential energies. We can relate the two energies by the following formula: 
. Thus, as kinetic energy decreases, potential energy increases. The only curve that shows this relationship is a linear curve with a negative slope.
The first paragraph helps us understand that a total amount of energy is fixed per molecule and is a combination of kinetic and potential energies. We can relate the two energies by the following formula:
Compare your answer with the correct one above
Current high levels of fossil fuel use, including coal-burning power plants and gasoline-powered automobiles, have helped contribute to the high concentrations of sulfur trioxide, SO3, found in the atmosphere. When sulfur trioxide and water interact, they can undergo the following chemical reaction to produce sulfuric acid, which is the main contributor to acid rain worldwide:
Acid rain showers are particularly common near coal-burning power plants and large cities. These showers are responsible for significant economic damage to sidewalks, roads, and buildings. Scientists interested in studying the effects of acid rain often use basic substances like calcium carbonate, the main component of limestone buildings, and expose them to varying volumes of acid rain to determine what volume of acid rain is necessary to begin to erode a building. A sample graph of one scientist’s experiment is replicated below:
Measuring acid and base levels is commonly done with a scale called pH, which uses the concentration of hydrogen ions to determine the acidity. Hydrogen ions are in a balance with hydroxide ions to give a scale with a range from 0 to 14. Values equal to or between 0 and 6.9 represent the acidic range where hydrogen ions predominate and values equal to or ranging from 7.1 and 14 represent the basic range where hydroxide ions predominate. Thus, the more hydrogen ions present, the more acidic the solution.
Scientists can tell when a titration (pH) experiment passes a certain pH using compounds called indicators. Indicators are usually colorless at pH levels below that of their specified color change. A table of indicators used by the above scientists and the pH at which they change colors is presented below.
The relationship between the concentrations of hydrogen and hydroxide ions in an acid-base solution may best be illustrated as which of the following?
Current high levels of fossil fuel use, including coal-burning power plants and gasoline-powered automobiles, have helped contribute to the high concentrations of sulfur trioxide, SO3, found in the atmosphere. When sulfur trioxide and water interact, they can undergo the following chemical reaction to produce sulfuric acid, which is the main contributor to acid rain worldwide:
Acid rain showers are particularly common near coal-burning power plants and large cities. These showers are responsible for significant economic damage to sidewalks, roads, and buildings. Scientists interested in studying the effects of acid rain often use basic substances like calcium carbonate, the main component of limestone buildings, and expose them to varying volumes of acid rain to determine what volume of acid rain is necessary to begin to erode a building. A sample graph of one scientist’s experiment is replicated below:
Measuring acid and base levels is commonly done with a scale called pH, which uses the concentration of hydrogen ions to determine the acidity. Hydrogen ions are in a balance with hydroxide ions to give a scale with a range from 0 to 14. Values equal to or between 0 and 6.9 represent the acidic range where hydrogen ions predominate and values equal to or ranging from 7.1 and 14 represent the basic range where hydroxide ions predominate. Thus, the more hydrogen ions present, the more acidic the solution.
Scientists can tell when a titration (pH) experiment passes a certain pH using compounds called indicators. Indicators are usually colorless at pH levels below that of their specified color change. A table of indicators used by the above scientists and the pH at which they change colors is presented below.
The relationship between the concentrations of hydrogen and hydroxide ions in an acid-base solution may best be illustrated as which of the following?
According to the paragraph below the passage graph, the number of hydrogen ions present in a solution is measured by a pH scale. The end of the paragraph tells us that when pH is low, the number of hydrogen ions is high and the number of hydroxide ions in low. In other words, when one is high, the other is low. This describes a reciprocal relationship.
According to the paragraph below the passage graph, the number of hydrogen ions present in a solution is measured by a pH scale. The end of the paragraph tells us that when pH is low, the number of hydrogen ions is high and the number of hydroxide ions in low. In other words, when one is high, the other is low. This describes a reciprocal relationship.
Compare your answer with the correct one above
The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.
Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.
Figure 1:
By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.
Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified.
Figure 2:
When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation:
Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.
Table 1:
Trial # Electric Charge Calculated in Coulombs (C) Vacuum Used? 1 1.602176487 x 10-8 No 2 1.602176487 x 10-2 Yes 3 1.602176487 x 10-6 No 4 1.602176487 x 10-4 Yes
Based only on the information in the passage, which of the following could be the charge of one electron?
I. 1.602176487 x 10-6 C
II. 1.602176487 x 10-2 C
III. 1.602176487 × 10-19 C
IV. 1.602176487 × 10-17 C
The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.
Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.
Figure 1:
By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.
Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified.
Figure 2:
When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation:
Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.
Table 1:
| Trial # | Electric Charge Calculated in Coulombs (C) | Vacuum Used? |
|---|---|---|
| 1 | 1.602176487 x 10-8 | No |
| 2 | 1.602176487 x 10-2 | Yes |
| 3 | 1.602176487 x 10-6 | No |
| 4 | 1.602176487 x 10-4 | Yes |
Based only on the information in the passage, which of the following could be the charge of one electron?
I. 1.602176487 x 10-6 C
II. 1.602176487 x 10-2 C
III. 1.602176487 × 10-19 C
IV. 1.602176487 × 10-17 C
The oil drops are suspended in the electric field by a charge that is equal to the net charge on the oil droplet. The passage and data table suggest that the oil drops all have total net charges that are multiples of either III or IV. This is because each electron on a drop has a charge that is some factor of the total net charge on the oil droplet. In other words, if there is one electron with charge X and you have 100 excess electrons, you will have a total charge of 100X. Based just on the information in the passage, the answer could be any number that is a factor of the observed values for the oil droplets.
The oil drops are suspended in the electric field by a charge that is equal to the net charge on the oil droplet. The passage and data table suggest that the oil drops all have total net charges that are multiples of either III or IV. This is because each electron on a drop has a charge that is some factor of the total net charge on the oil droplet. In other words, if there is one electron with charge X and you have 100 excess electrons, you will have a total charge of 100X. Based just on the information in the passage, the answer could be any number that is a factor of the observed values for the oil droplets.
Compare your answer with the correct one above
The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.
Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.
Figure 1:
By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.
Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified.
Figure 2:
When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation:
Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.
Table 1:
Trial # Electric Charge Calculated in Coulombs (C) Vacuum Used? 1 1.602176487 x 10-8 No 2 1.602176487 x 10-2 Yes 3 1.602176487 x 10-6 No 4 1.602176487 x 10-4 Yes
Changes to which of the following would likely result in a difference in the observed strength of the electric field needed to suspend an oil drop?
The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.
Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.
Figure 1:
By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.
Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified.
Figure 2:
When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation:
Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.
Table 1:
| Trial # | Electric Charge Calculated in Coulombs (C) | Vacuum Used? |
|---|---|---|
| 1 | 1.602176487 x 10-8 | No |
| 2 | 1.602176487 x 10-2 | Yes |
| 3 | 1.602176487 x 10-6 | No |
| 4 | 1.602176487 x 10-4 | Yes |
Changes to which of the following would likely result in a difference in the observed strength of the electric field needed to suspend an oil drop?
The experiment is fundamentally matching the net electric charge on the oil drop with an external electric field to exactly counteract the force of gravity. As a result, changes to any of these quantities will change the observed results.
The experiment is fundamentally matching the net electric charge on the oil drop with an external electric field to exactly counteract the force of gravity. As a result, changes to any of these quantities will change the observed results.
Compare your answer with the correct one above
The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.
Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.
Figure 1:
By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.
Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified.
Figure 2:
When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation:
Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.
Table 1:
Trial # Electric Charge Calculated in Coulombs (C) Vacuum Used? 1 1.602176487 x 10-8 No 2 1.602176487 x 10-2 Yes 3 1.602176487 x 10-6 No 4 1.602176487 x 10-4 Yes
In Trial 1 and 3, the additional net force not present in Trial 2 and 4 is most probably acting:
The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.
Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.
Figure 1:
By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.
Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified.
Figure 2:
When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation:
Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.
Table 1:
| Trial # | Electric Charge Calculated in Coulombs (C) | Vacuum Used? |
|---|---|---|
| 1 | 1.602176487 x 10-8 | No |
| 2 | 1.602176487 x 10-2 | Yes |
| 3 | 1.602176487 x 10-6 | No |
| 4 | 1.602176487 x 10-4 | Yes |
In Trial 1 and 3, the additional net force not present in Trial 2 and 4 is most probably acting:
The additional force in the absence of a vacuum is mainly air resistance, and the magnitude of the observed electric force suggests that the net force is acting parallel and opposite to gravity. Thus, it is in the same direction as the electric force.
The additional force in the absence of a vacuum is mainly air resistance, and the magnitude of the observed electric force suggests that the net force is acting parallel and opposite to gravity. Thus, it is in the same direction as the electric force.
Compare your answer with the correct one above
The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.
Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.
Figure 1:
By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.
Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified.
Figure 2:
When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation:
Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.
Table 1:
Trial # Electric Charge Calculated in Coulombs (C) Vacuum Used? 1 1.602176487 x 10-8 No 2 1.602176487 x 10-2 Yes 3 1.602176487 x 10-6 No 4 1.602176487 x 10-4 Yes
The electric force experienced by oil drops will vary directly with the magnitude of charge on the drop. A scientist is measuring two different drops in two different experimental apparatuses, but each in perfect suspension and not moving. Drop 1 has a greater net charge than does drop 2. The magnitude of the electric force:
The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.
Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.
Figure 1:
By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.
Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified.
Figure 2:
When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation:
Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.
Table 1:
| Trial # | Electric Charge Calculated in Coulombs (C) | Vacuum Used? |
|---|---|---|
| 1 | 1.602176487 x 10-8 | No |
| 2 | 1.602176487 x 10-2 | Yes |
| 3 | 1.602176487 x 10-6 | No |
| 4 | 1.602176487 x 10-4 | Yes |
The electric force experienced by oil drops will vary directly with the magnitude of charge on the drop. A scientist is measuring two different drops in two different experimental apparatuses, but each in perfect suspension and not moving. Drop 1 has a greater net charge than does drop 2. The magnitude of the electric force:
The electric force, in isolation, will be greater on drop 1 because it has a greater net charge to interact with the external electric field.
The electric force, in isolation, will be greater on drop 1 because it has a greater net charge to interact with the external electric field.
Compare your answer with the correct one above
The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.
Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.
Figure 1:
By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.
Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified.
Figure 2:
When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation:
Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.
Table 1:
Trial # Electric Charge Calculated in Coulombs (C) Vacuum Used? 1 1.602176487 x 10-8 No 2 1.602176487 x 10-2 Yes 3 1.602176487 x 10-6 No 4 1.602176487 x 10-4 Yes
Which of the following statements is most consistent with the findings of this experiment?
The Millikin oil drop experiment is among the most important experiments in the history of science. It was used to determine one of the fundamental constants of the universe, the charge on the electron. For his work, Robert Millikin won the Nobel Prize in Physics in 1923.
Millikin used an experimental setup as follows in Figure 1. He opened a chamber of oil into an adjacent uniform electric field. The oil droplets sank into the electric field once the trap door opened, but were then immediately suspended by the forces of electricity present in the field.
Figure 1:
By determining how much force was needed to exactly counteract the gravity pulling the oil droplet down, Millikin was able to determine the force of electricity. This is depicted in Figure 2.
Using this information, he was able to calculate the exact charge on an electron. By changing some conditions, such as creating a vacuum in the apparatus, the experiment can be modified.
Figure 2:
When the drop is suspended perfectly, the total forces up equal the total forces down. Because Millikin knew the electric field in the apparatus, the force of air resistance, the mass of the drop, and the acceleration due to gravity, he was able to solve the following equation:
Table 1 summarizes the electric charge found on oil drops in suspension. Millikin correctly concluded that the calculated charges must all be multiples of the fundamental charge of the electron. A hypothetical oil drop contains some net charge due to lost electrons, and this net charge cannot be smaller than the charge on a single electron.
Table 1:
| Trial # | Electric Charge Calculated in Coulombs (C) | Vacuum Used? |
|---|---|---|
| 1 | 1.602176487 x 10-8 | No |
| 2 | 1.602176487 x 10-2 | Yes |
| 3 | 1.602176487 x 10-6 | No |
| 4 | 1.602176487 x 10-4 | Yes |
Which of the following statements is most consistent with the findings of this experiment?
The data presented in the passage suggest that the fundamental charge on an electron must be a factor of the observed charge on the entire oil drop. While this value can change, the fundamental charge on all electrons will be identical.
The data presented in the passage suggest that the fundamental charge on an electron must be a factor of the observed charge on the entire oil drop. While this value can change, the fundamental charge on all electrons will be identical.
Compare your answer with the correct one above
A student wants to perform an experiment that tests the relationship between the pressure of a gas and the volume it occupies. To perform this experiment, the student places a specific type of gas in a sealed chamber that can change pressure and that can adapt its volume to the gas within it. The chamber also adjusts to the changing pressure such that the temperature (which also has an effect on gas volume) does not change. The following data was obtained:
In Trial 4, the chamber used in the experiment malfunctioned and there was a slight decrease in temperature, leading to a faulty reading of volume for Trial 4. Given this information, what can we say about the relationship between the temperature of a gas and its volume?
A student wants to perform an experiment that tests the relationship between the pressure of a gas and the volume it occupies. To perform this experiment, the student places a specific type of gas in a sealed chamber that can change pressure and that can adapt its volume to the gas within it. The chamber also adjusts to the changing pressure such that the temperature (which also has an effect on gas volume) does not change. The following data was obtained:
In Trial 4, the chamber used in the experiment malfunctioned and there was a slight decrease in temperature, leading to a faulty reading of volume for Trial 4. Given this information, what can we say about the relationship between the temperature of a gas and its volume?
This is a tricky question. First we must estimate what the correct reading for Trial 4 should have been to see how the decrease in temperature affected the volume. Using mental math, we can deduce that the volume reading for Trial 4 should have been about 22.4/2.5 or (multiplying both the denominator and numerator by 4) 89.6/10 or essentially 9. Since the actual reading was 8.2 Liters, we know that the decrease in temperature decreased the volume, implying a direct relationship. That is, as one goes up, the other goes up, and vice versa. However our work is not done. Since we do not know by how much the temperature changed, we cannot make a call as to whether the relationship is linear or exponential. Therefore, the correct answer is that it is simply directly related.
This is a tricky question. First we must estimate what the correct reading for Trial 4 should have been to see how the decrease in temperature affected the volume. Using mental math, we can deduce that the volume reading for Trial 4 should have been about 22.4/2.5 or (multiplying both the denominator and numerator by 4) 89.6/10 or essentially 9. Since the actual reading was 8.2 Liters, we know that the decrease in temperature decreased the volume, implying a direct relationship. That is, as one goes up, the other goes up, and vice versa. However our work is not done. Since we do not know by how much the temperature changed, we cannot make a call as to whether the relationship is linear or exponential. Therefore, the correct answer is that it is simply directly related.
Compare your answer with the correct one above
A student wants to perform an experiment which tests the relationship between the pressure of a gas and the volume it occupies. To perform this experiment, the student places a specific type of gas in a sealed chamber that can change pressure and which can adapt its volume to the gas within it. The chamber also adjusts to the changing pressure such that the temperature (which also has an effect on gas volume) does not change. The following data was obtained:
In a second experiment, the student tries the same experiment described in the pre-question text and uses a different gas for each trial. If the readings for volume yielded the same results, what could be said about the relationship between type of gas and volume?
A student wants to perform an experiment which tests the relationship between the pressure of a gas and the volume it occupies. To perform this experiment, the student places a specific type of gas in a sealed chamber that can change pressure and which can adapt its volume to the gas within it. The chamber also adjusts to the changing pressure such that the temperature (which also has an effect on gas volume) does not change. The following data was obtained:
In a second experiment, the student tries the same experiment described in the pre-question text and uses a different gas for each trial. If the readings for volume yielded the same results, what could be said about the relationship between type of gas and volume?
The correct answer is that there is no relationship. As type of gas was one of the variables held constant in the first experiment, once the type of gas was no longer held constant, we would expect different results than those that experiment one yielded; however, since the data came out the same, we can safely conclude that there is no observable relationship between type of gas and volume.
The correct answer is that there is no relationship. As type of gas was one of the variables held constant in the first experiment, once the type of gas was no longer held constant, we would expect different results than those that experiment one yielded; however, since the data came out the same, we can safely conclude that there is no observable relationship between type of gas and volume.
Compare your answer with the correct one above
The above chemical equation describes the dissociation of carbonic acid 
into bicarbonate 
and hydrogen ion 
. A chemistry student wants to study the behavior of carbonic acid, as it is a part of one of the most important physiological control systems in the human body.
When carbon dioxide 
enters the blood in your body, it takes on the form of carbonic acid. Carbonic acid is in what we call "equilibrium"with bicarbonate ion and hydrogen ion. This equilibrium functions in the following manner: if more carbonic acid is present, more will dissociate into bicarbonate and hydrogen ion. On the other hand, if there is more bicarbonate and/or hydrogen ion, we say that equilibrium as shown in the above equation will "shift left" and more carbonic acid will be produced from bicarbonate and hydrogen.
To study this effect, the student obtains a mixture of carbonic acid, bicarbonate, and hydrogen ion. Next, the student conducts trials in which she adds a certain amount of one of the chemicals one at a time and then measures how the concentrations of each chemical change after each addition.
pH is a measure of hydrogen ion concentration and is used to measure acidity. A pH of 7 is neutral, while a low pH corresponds to a high concentration of hydrogen ions, or an acid. What can we infer would happen to the pH of a person's blood if a large amount of carbon dioxide were to be produced in that person's body, such as during exercise?
The above chemical equation describes the dissociation of carbonic acid
When carbon dioxide
To study this effect, the student obtains a mixture of carbonic acid, bicarbonate, and hydrogen ion. Next, the student conducts trials in which she adds a certain amount of one of the chemicals one at a time and then measures how the concentrations of each chemical change after each addition.
pH is a measure of hydrogen ion concentration and is used to measure acidity. A pH of 7 is neutral, while a low pH corresponds to a high concentration of hydrogen ions, or an acid. What can we infer would happen to the pH of a person's blood if a large amount of carbon dioxide were to be produced in that person's body, such as during exercise?
The correct answer is that this person's blood pH would decrease. With more carbon dioxide in the blood, as the passage states, more carbonic acid would be present. Therefore, according to the passage's description of equilibrium, equilibrium would shift right and produce more bicarbonate and hydrogen ions. This would increase the concentration of hydrogen and therefore lower the pH.
The correct answer is that this person's blood pH would decrease. With more carbon dioxide in the blood, as the passage states, more carbonic acid would be present. Therefore, according to the passage's description of equilibrium, equilibrium would shift right and produce more bicarbonate and hydrogen ions. This would increase the concentration of hydrogen and therefore lower the pH.
Compare your answer with the correct one above
The above chemical equation describes the dissociation of carbonic acid into bicarbonate and hydrogen ion . A chemistry student wants to study the behavior of carbonic acid, as it is a part of one of the most important physiological control systems in the human body.
When carbon dioxide enters the blood in your body, it takes on the form of carbonic acid. Carbonic acid is in what we call "equilibrium"with bicarbonate ion and hydrogen ion. This equilibrium functions in the following manner: if more carbonic acid is present, more will dissociate into bicarbonate and hydrogen ion. On the other hand, if there is more bicarbonate and/or hydrogen ion, we say that equilibrium as shown in the above equation will "shift left" and more carbonic acid will be produced from bicarbonate and hydrogen.
To study this effect, the student obtains a mixture of carbonic acid, bicarbonate, and hydrogen ion. Next, the student conducts trials in which she adds a certain amount of one of the chemicals one at a time and then measures how the concentrations of each chemical change after each addition.
What can we infer would happen to one of the student's trials if the student added both bicarbonate ion and hydrogen ion to that trial?
The above chemical equation describes the dissociation of carbonic acid
When carbon dioxide
To study this effect, the student obtains a mixture of carbonic acid, bicarbonate, and hydrogen ion. Next, the student conducts trials in which she adds a certain amount of one of the chemicals one at a time and then measures how the concentrations of each chemical change after each addition.
What can we infer would happen to one of the student's trials if the student added both bicarbonate ion and hydrogen ion to that trial?
If the student adds either bicarbonate ion or hydrogen ion, we know that the equation's equilibrium will shift to the left. So, it is reasonable to assume that if the student adds both bicarbonate ion and hydrogen ion to the trial, the reaction will shift farther to the left than if the student had only added one of the reactants.
If the student adds either bicarbonate ion or hydrogen ion, we know that the equation's equilibrium will shift to the left. So, it is reasonable to assume that if the student adds both bicarbonate ion and hydrogen ion to the trial, the reaction will shift farther to the left than if the student had only added one of the reactants.
Compare your answer with the correct one above
Two scientists wanted to test the solubility of different substances. Solubility is a measure of how many moles of a given substance (known as the solute) can dissolve in a given volume of another substance (known as the solvent). The solvent can also be thought of as the substance present in greater amount, while the solute can be seen as the substance present in lesser amount. The scientists performed the following experiments to investigate this property.
Experiment 1
The scientists tested the number of moles of several substances that could be completely dissolved in 
of water at various temperatures. They made their solutions by slowly adding amounts of each substance to beakers sitting on a hot plate containing water and a stirring rod until no more of the substance dissolved in the solution. The beakers were weighed before and after the additions and the difference in mass was calculated to be the added mass of the substance. The researchers then calculated the number of moles that dissolved for each trial using the molecular mass and the recorded mass for each trial. Results are recorded in Table 1.
Table 1
Experiment 2
In this experiment, the scientists wanted to test the solubility of 
in a variety of liquids at several temperatures. Their procedure was similar to that of Experiment 1, but with a range of liquids and only one solid. The results are compiled in Table 2.
Table 2
In Experiment 2, which of the following combinations of temperature and solvent dissolved the greatest number of moles of 
?
Two scientists wanted to test the solubility of different substances. Solubility is a measure of how many moles of a given substance (known as the solute) can dissolve in a given volume of another substance (known as the solvent). The solvent can also be thought of as the substance present in greater amount, while the solute can be seen as the substance present in lesser amount. The scientists performed the following experiments to investigate this property.
Experiment 1
The scientists tested the number of moles of several substances that could be completely dissolved in
Table 1
Experiment 2
In this experiment, the scientists wanted to test the solubility of
Table 2
In Experiment 2, which of the following combinations of temperature and solvent dissolved the greatest number of moles of
To find the correct answer to this question, we need to look for it in Table 2. We are asked to find the greatest number of moles of 
that dissolved. Begin by searching in the last column until you find the largest value. Then, look at the temperature and solvent corresponding to that value and see if any answer choices match what you found.
In this case, the largest number of moles dissolved is 
. This corresponds with 
at 
, which is in fact one of our answer choices.
To find the correct answer to this question, we need to look for it in Table 2. We are asked to find the greatest number of moles of
In this case, the largest number of moles dissolved is
Compare your answer with the correct one above
Two scientists wanted to test the solubility of different substances. Solubility is a measure of how many moles of a given substance (known as the solute) can dissolve in a given volume of another substance (known as the solvent). The solvent can also be thought of as the substance present in greater amount, while the solute can be seen as the substance present in lesser amount. The scientists performed the following experiments to investigate this property.
Experiment 1
The scientists tested the number of moles of several substances that could be completely dissolved in of water at various temperatures. They made their solutions by slowly adding amounts of each substance to beakers sitting on a hot plate containing water and a stirring rod until no more of the substance dissolved in the solution. The beakers were weighed before and after the additions and the difference in mass was calculated to be the added mass of the substance. The researchers then calculated the number of moles that dissolved for each trial using the molecular mass and the recorded mass for each trial. Results are recorded in Table 1.
Table 1
Experiment 2
In this experiment, the scientists wanted to test the solubility of in a variety of liquids at several temperatures. Their procedure was similar to that of Experiment 1, but with a range of liquids and only one solid. The results are compiled in Table 2.
Table 2
Which of the following correctly ranks the solutes from Experiment 1 in decreasing order of solubility in water at 
?
Two scientists wanted to test the solubility of different substances. Solubility is a measure of how many moles of a given substance (known as the solute) can dissolve in a given volume of another substance (known as the solvent). The solvent can also be thought of as the substance present in greater amount, while the solute can be seen as the substance present in lesser amount. The scientists performed the following experiments to investigate this property.
Experiment 1
The scientists tested the number of moles of several substances that could be completely dissolved in
Table 1
Experiment 2
In this experiment, the scientists wanted to test the solubility of
Table 2
Which of the following correctly ranks the solutes from Experiment 1 in decreasing order of solubility in water at
The introduction explains that solubility is a measure of how many moles of a substance can dissolve in a given volume of another substance. This is a very important clue that tells us we need to focus on the "moles added" column rather than the "grams added" column. We need to rank our substances in decreasing order, so we need start with the one with the highest solubility at 
.
The number of moles dissolved at 
are as follows.
: 
: 
: 
: 
So the correct order is:
The introduction explains that solubility is a measure of how many moles of a substance can dissolve in a given volume of another substance. This is a very important clue that tells us we need to focus on the "moles added" column rather than the "grams added" column. We need to rank our substances in decreasing order, so we need start with the one with the highest solubility at
The number of moles dissolved at
So the correct order is:
Compare your answer with the correct one above
Two scientists wanted to test the solubility of different substances. Solubility is a measure of how many moles of a given substance (known as the solute) can dissolve in a given volume of another substance (known as the solvent). The solvent can also be thought of as the substance present in greater amount, while the solute can be seen as the substance present in lesser amount. The scientists performed the following experiments to investigate this property.
Experiment 1
The scientists tested the number of moles of several substances that could be completely dissolved in of water at various temperatures. They made their solutions by slowly adding amounts of each substance to beakers sitting on a hot plate containing water and a stirring rod until no more of the substance dissolved in the solution. The beakers were weighed before and after the additions and the difference in mass was calculated to be the added mass of the substance. The researchers then calculated the number of moles that dissolved for each trial using the molecular mass and the recorded mass for each trial. Results are recorded in Table 1.
Table 1
Experiment 2
In this experiment, the scientists wanted to test the solubility of in a variety of liquids at several temperatures. Their procedure was similar to that of Experiment 1, but with a range of liquids and only one solid. The results are compiled in Table 2.
Table 2
Which of the following best explains the relationship between temperature and solubility of 
?
Two scientists wanted to test the solubility of different substances. Solubility is a measure of how many moles of a given substance (known as the solute) can dissolve in a given volume of another substance (known as the solvent). The solvent can also be thought of as the substance present in greater amount, while the solute can be seen as the substance present in lesser amount. The scientists performed the following experiments to investigate this property.
Experiment 1
The scientists tested the number of moles of several substances that could be completely dissolved in
Table 1
Experiment 2
In this experiment, the scientists wanted to test the solubility of
Table 2
Which of the following best explains the relationship between temperature and solubility of
This question doesn't tell us where to look, but it tells us we need to be concerned with solubility of 
. Experiment 1 is the only place where 
is mentioned, so begin there. In Table 1, the entries for moles of 
are highest at 
, and lower for increasing temperature. This means that temperature and solubility are indirectly related; as one increases, the other decreases. Thus, our correct answer is, "As temperature decreases, solubility of 
increases," because our solubility is highest at lower temperatures.
This question doesn't tell us where to look, but it tells us we need to be concerned with solubility of
Compare your answer with the correct one above