Cosine - ACT Math
Card 0 of 20

If angle A measures 30 degrees and the hypotenuse is 4, what is the length of AB in the given right triangle?

If angle A measures 30 degrees and the hypotenuse is 4, what is the length of AB in the given right triangle?
Cosine A = Adjacent / Hypotenuse = AB / AC = AB / 4
Cosine A = AB / 4
Cos (30º) = √3 / 2 = AB / 4
Solve for AB
√3 / 2 = AB / 4
AB = 4 * (√3 / 2) = 2√3
Cosine A = Adjacent / Hypotenuse = AB / AC = AB / 4
Cosine A = AB / 4
Cos (30º) = √3 / 2 = AB / 4
Solve for AB
√3 / 2 = AB / 4
AB = 4 * (√3 / 2) = 2√3
Compare your answer with the correct one above
To solve this problem you need to make the triangle that the problem is talking about. Cosine is equal to the adjacent side over the hypotenuse of a right triangle

So this is what our triangle looks like:

Now use the pythagorean theorem to find the other side: 


Sine is equal to the opposite side over the hypotenuse, the opposite side is 12


To solve this problem you need to make the triangle that the problem is talking about. Cosine is equal to the adjacent side over the hypotenuse of a right triangle
So this is what our triangle looks like:

Now use the pythagorean theorem to find the other side:
Sine is equal to the opposite side over the hypotenuse, the opposite side is 12
Compare your answer with the correct one above
The hypotenuse of right triangle HLM shown below is  long. The cosine of angle
long. The cosine of angle  is
is  . How many inches long is
. How many inches long is  ?
?

The hypotenuse of right triangle HLM shown below is 




Remember that 
Then, we can set up the equation using the given information.

Now, solve for  .
.


Remember that
Then, we can set up the equation using the given information.
Now, solve for 
Compare your answer with the correct one above
A man has a rope that is  long, attached to the top of a small building. He pegs the rope into the ground at an angle of
long, attached to the top of a small building. He pegs the rope into the ground at an angle of  . How far away from the building did he walk horizontally to attach the rope to the ground? Round to the nearest inch.
. How far away from the building did he walk horizontally to attach the rope to the ground? Round to the nearest inch.
A man has a rope that is 

Begin by drawing out this scenario using a little right triangle:

We know that the cosine of an angle is equal to the ratio of the side adjacent to that angle to the hypotenuse of the triangle. Thus, for our triangle, we know:

Using your calculator, solve for  :
:

This is  . Now, take the decimal portion in order to find the number of inches involved.
. Now, take the decimal portion in order to find the number of inches involved.

Thus, rounded, your answer is  feet and
feet and  inches.
inches.
Begin by drawing out this scenario using a little right triangle:

We know that the cosine of an angle is equal to the ratio of the side adjacent to that angle to the hypotenuse of the triangle. Thus, for our triangle, we know:
Using your calculator, solve for 
This is 
Thus, rounded, your answer is 

Compare your answer with the correct one above

What is  in the right triangle above? Round to the nearest hundredth.
in the right triangle above? Round to the nearest hundredth.

What is 
Recall that the cosine of an angle is the ratio of the adjacent side to the hypotenuse of that triangle. Thus, for this triangle, we can say:

Solving for  , we get:
, we get:

 or
or 
Recall that the cosine of an angle is the ratio of the adjacent side to the hypotenuse of that triangle. Thus, for this triangle, we can say:
Solving for 

Compare your answer with the correct one above
An airline pilot must know the exact vertical height of his plane above the runway to know when to extend the landing gear under the nose. If the nose of the plane is  feet away from the ground and the plane is descending at an angle of
feet away from the ground and the plane is descending at an angle of  to the vertical, how far above the ground to the nearest
to the vertical, how far above the ground to the nearest  foot is the landing gear?
foot is the landing gear?
(Ignore the height of the plane itself).
An airline pilot must know the exact vertical height of his plane above the runway to know when to extend the landing gear under the nose. If the nose of the plane is 


(Ignore the height of the plane itself).
The plane itself is effectively at the top of a right triangle, with topmost angle  and hypotenuse
and hypotenuse  feet. If this is the case, then SOHCAHTOA tells us that
feet. If this is the case, then SOHCAHTOA tells us that  .
.
Now, solve for the adjacent:

Thus, our plane's nose is approximately  feet from the runway.
feet from the runway.
The plane itself is effectively at the top of a right triangle, with topmost angle 


Now, solve for the adjacent:
Thus, our plane's nose is approximately 
Compare your answer with the correct one above

In the right triangle shown above, what is the  ?
?

In the right triangle shown above, what is the 
Use SOH-CAH-TOA to solve for the sine of a given angle. This stands for:


 .
.
From our triangle we see that at point  , the adjacent side is side
, the adjacent side is side  and the hypotenuse doesn't depend upon position, it's always
and the hypotenuse doesn't depend upon position, it's always  . Thus we get that
. Thus we get that 

Use SOH-CAH-TOA to solve for the sine of a given angle. This stands for:

From our triangle we see that at point 



Compare your answer with the correct one above
In a given right triangle  , hypotenuse
, hypotenuse  and
and  . Using the definition of
. Using the definition of  , find the length of leg
, find the length of leg  . Round all calculations to the nearest tenth.
. Round all calculations to the nearest tenth.
In a given right triangle 




In right triangles, SOHCAHTOA tells us that  , and we know that
, and we know that  and hypotenuse
and hypotenuse  . Therefore, a simple substitution and some algebra gives us our answer.
. Therefore, a simple substitution and some algebra gives us our answer.

 Use a calculator or reference to approximate cosine.
Use a calculator or reference to approximate cosine.
 Isolate the variable term.
Isolate the variable term.
Thus,  .
.
In right triangles, SOHCAHTOA tells us that 




Thus, 
Compare your answer with the correct one above
In a given right triangle  , hypotenuse
, hypotenuse  and
and  . Using the definition of
. Using the definition of  , find the length of leg
, find the length of leg  . Round all calculations to the nearest hundredth.
. Round all calculations to the nearest hundredth.
In a given right triangle 




In right triangles, SOHCAHTOA tells us that  , and we know that
, and we know that  and hypotenuse
and hypotenuse  . Therefore, a simple substitution and some algebra gives us our answer.
. Therefore, a simple substitution and some algebra gives us our answer.

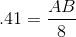 Use a calculator or reference to approximate cosine.
Use a calculator or reference to approximate cosine.
 Isolate the variable term.
Isolate the variable term.
Thus,  .
.
In right triangles, SOHCAHTOA tells us that 


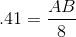

Thus, 
Compare your answer with the correct one above
In a given right triangle  , hypotenuse
, hypotenuse  and
and  . Using the definition of
. Using the definition of  , find the length of leg
, find the length of leg  . Round all calculations to the nearest tenth.
. Round all calculations to the nearest tenth.
In a given right triangle 




In right triangles, SOHCAHTOA tells us that  , and we know that
, and we know that  and hypotenuse
and hypotenuse  . Therefore, a simple substitution and some algebra gives us our answer.
. Therefore, a simple substitution and some algebra gives us our answer.

 Use a calculator or reference to approximate cosine.
Use a calculator or reference to approximate cosine.
 Isolate the variable term.
Isolate the variable term.
Thus,  .
.
In right triangles, SOHCAHTOA tells us that 




Thus, 
Compare your answer with the correct one above
Edgar is standing at the top of a 35-foot long slide. He knows that the angle between the top of the slide and the ladder that he climbed to reach the top is 68 degrees. If the ladder meets the ground at a right angle, how far did Edgar climb?
Edgar is standing at the top of a 35-foot long slide. He knows that the angle between the top of the slide and the ladder that he climbed to reach the top is 68 degrees. If the ladder meets the ground at a right angle, how far did Edgar climb?
Edgar is standing on top of a right triangle because the angle from the vertical ladder to the ground is 90 degrees. To solve this question, you must know SOHCAHTOA. This acronym can be broken into three parts to solve for the sine, cosine, and tangent.



In order to solve for the missing side, you need to choose the trigonometric function that includes the side you need to find and the side that you know, relative to the angle that you know. In this case, you know the hypotenuse, so you would not use the tangent function; furthermore, you are looking for the side that is adjacent to the 68-degree angle. Thus, you need the function that incorporates adjacent and hypotenuse—the cosine function.



Typically, you would use a calculator at this point to calculate the cosine function; however, based on the answer choices provided, you can stop at this point.
Edgar is standing on top of a right triangle because the angle from the vertical ladder to the ground is 90 degrees. To solve this question, you must know SOHCAHTOA. This acronym can be broken into three parts to solve for the sine, cosine, and tangent.
In order to solve for the missing side, you need to choose the trigonometric function that includes the side you need to find and the side that you know, relative to the angle that you know. In this case, you know the hypotenuse, so you would not use the tangent function; furthermore, you are looking for the side that is adjacent to the 68-degree angle. Thus, you need the function that incorporates adjacent and hypotenuse—the cosine function.
Typically, you would use a calculator at this point to calculate the cosine function; however, based on the answer choices provided, you can stop at this point.
Compare your answer with the correct one above

In the above triangle,  and
and  . Find
. Find  .
.

In the above triangle, 


With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the adjacent and hypotenuse sides of the triangle with relation to the angle. With this information, we can use the cosine function to find the angle.




With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the adjacent and hypotenuse sides of the triangle with relation to the angle. With this information, we can use the cosine function to find the angle.
Compare your answer with the correct one above

For the above triangle,  and
and  . Find
. Find  .
.

For the above triangle, 


With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the adjacent and hypotenuse sides of the triangle with relation to the angle. With this information, we can use the cosine function to find the angle.




With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the adjacent and hypotenuse sides of the triangle with relation to the angle. With this information, we can use the cosine function to find the angle.
Compare your answer with the correct one above

For the above triangle,  and
and  . Find
. Find  .
.

For the above triangle, 


With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the adjacent and hypotenuse sides of the triangle with relation to the angle. However, if we plug the given values into the formula for cosine, we get:



This problem does not have a solution. The sides of a right triangle must be shorter than the hypotenuse. A triangle with a side longer than the hypotenuse cannot exist. Similarly, the domain of the arccos function is ![\left [ -1, 1\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/272522/gif.latex) . It is not defined at 1.3.
. It is not defined at 1.3.
With right triangles, we can use SOH CAH TOA to solve for unknown side lengths and angles. For this problem, we are given the adjacent and hypotenuse sides of the triangle with relation to the angle. However, if we plug the given values into the formula for cosine, we get:
This problem does not have a solution. The sides of a right triangle must be shorter than the hypotenuse. A triangle with a side longer than the hypotenuse cannot exist. Similarly, the domain of the arccos function is ![\left [ -1, 1\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/272522/gif.latex)
Compare your answer with the correct one above
A  rope is thrown down from a building to the ground and tied up at a distance of
rope is thrown down from a building to the ground and tied up at a distance of  from the base of the building. What is the angle measure between the rope and the ground? Round to the nearest hundredth of a degree_._
from the base of the building. What is the angle measure between the rope and the ground? Round to the nearest hundredth of a degree_._
A 

You can draw your scenario using the following right triangle:

Recall that the cosine of an angle is equal to the ratio of the adjacent side to the hypotenuse of the triangle. You can solve for the angle by using an inverse cosine function:
 or
or  degrees.
degrees.
You can draw your scenario using the following right triangle:

Recall that the cosine of an angle is equal to the ratio of the adjacent side to the hypotenuse of the triangle. You can solve for the angle by using an inverse cosine function:


Compare your answer with the correct one above

What is the value of  in the right triangle above? Round to the nearest hundredth of a degree.
in the right triangle above? Round to the nearest hundredth of a degree.

What is the value of 
Recall that the cosine of an angle is equal to the ratio of the adjacent side to the hypotenuse of the triangle. You can solve for the angle by using an inverse cosine function:
 or
or  .
.
Recall that the cosine of an angle is equal to the ratio of the adjacent side to the hypotenuse of the triangle. You can solve for the angle by using an inverse cosine function:


Compare your answer with the correct one above
A support beam (buttress) lies against a building under construction. If the beam is  feet long and strikes the building at a point
feet long and strikes the building at a point  feet up the wall, what angle does the beam strike the building at? Round to the nearest degree.
feet up the wall, what angle does the beam strike the building at? Round to the nearest degree.
A support beam (buttress) lies against a building under construction. If the beam is 

Our answer lies in inverse functions. If the buttress is  feet long and is
feet long and is  feet up the ladder at the desired angle, then:
feet up the ladder at the desired angle, then:

Thus, using inverse functions we can say that 
Thus, our buttress strikes the buliding at approximately a  angle.
angle.
Our answer lies in inverse functions. If the buttress is 

Thus, using inverse functions we can say that
Thus, our buttress strikes the buliding at approximately a 
Compare your answer with the correct one above
A stone monument stands as a tourist attraction. A tourist wants to catch the sun at just the right angle to "sit" on top of the pillar. The tourist lies down on the ground  meters away from the monument, points the camera at the top of the monument, and the camera's display reads "DISTANCE --
meters away from the monument, points the camera at the top of the monument, and the camera's display reads "DISTANCE --  METERS". To the nearest
METERS". To the nearest  degree, what angle is the sun at relative to the horizon?
degree, what angle is the sun at relative to the horizon?
A stone monument stands as a tourist attraction. A tourist wants to catch the sun at just the right angle to "sit" on top of the pillar. The tourist lies down on the ground 


Our answer lies in inverse functions. If the monument is  meters away and the camera is
meters away and the camera is  meters from the monument's top at the desired angle, then:
meters from the monument's top at the desired angle, then:

Thus, using inverse functions we can say that 
Thus, our buttress strikes the buliding at approximately a  angle.
angle.
Our answer lies in inverse functions. If the monument is 

Thus, using inverse functions we can say that
Thus, our buttress strikes the buliding at approximately a 
Compare your answer with the correct one above
What is the cosine of the angle formed between the origin and the point  if that angle is formed with one side of the angle beginning on the
if that angle is formed with one side of the angle beginning on the  -axis and then rotating counter-clockwise to
-axis and then rotating counter-clockwise to  ? Round to the nearest hundredth.
? Round to the nearest hundredth.
What is the cosine of the angle formed between the origin and the point 


Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the  -axis as your reference point for your angle. (Hence, it is called the "reference angle.") Now, it is easiest to think of this like you are drawing a little triangle in the second quadrant of the Cartesian plane. It would look like:
-axis as your reference point for your angle. (Hence, it is called the "reference angle.") Now, it is easiest to think of this like you are drawing a little triangle in the second quadrant of the Cartesian plane. It would look like:

So, you first need to calculate the hypotenuse:

So, the cosine of an angle is:
 or, for your data,
or, for your data,  .
.
This is approximately  . Rounding, this is
. Rounding, this is  . However, since
. However, since  is in the second quadrant your value must be negative:
is in the second quadrant your value must be negative:  .
.
Recall that when you calculate a trigonometric function for an obtuse angle like this, you always use the 

So, you first need to calculate the hypotenuse:
So, the cosine of an angle is:


This is approximately 



Compare your answer with the correct one above
If  and
and  , what is the value of
, what is the value of  ?
?
If 


Based on this data, we can make a little triangle that looks like:

This is because  .
.
Now, this means that  must equal
must equal  . (Recall that the cosine function is negative in the second quadrant.) Now, we are looking for:
. (Recall that the cosine function is negative in the second quadrant.) Now, we are looking for:
 or
or  . This is the cosine of a reference angle of:
. This is the cosine of a reference angle of:

Looking at our little triangle above, we can see that the cosine of  is
is  .
.
Based on this data, we can make a little triangle that looks like:

This is because 
Now, this means that 



Looking at our little triangle above, we can see that the cosine of 

Compare your answer with the correct one above




