Acute / Obtuse Triangles - ACT Math

Card 0 of 20

Question

Points A, B, C, D are collinear. The measure of ∠ DCE is 130° and of ∠ AEC is 80°. Find the measure of ∠ EAD.

Answer

To solve this question, you need to remember that the sum of the angles in a triangle is 180°. You also need to remember supplementary angles. If you know what ∠ DCE is, you also know what ∠ ECA is. Hence you know two angles of the triangle, 180°-80°-50°= 50°.

Compare your answer with the correct one above

Question

In the triangle below, AB=BC (figure is not to scale) . If angle A is 41°, what is the measure of angle B?

A (Angle A = 41°)

B C

Answer

If angle A is 41°, then angle C must also be 41°, since AB=BC. So, the sum of these 2 angles is:

41° + 41° = 82°

Since the sum of the angles in a triangle is 180°, you can find out the measure of the remaining angle by subtracting 82 from 180:

180° - 82° = 98°

Compare your answer with the correct one above

Question

Points A, B, and C are collinear (they lie along the same line). The measure of angle CAD is $30^{\circ}$ . The measure of angle CBD is $60^{\circ}$ . The length of segment $\overline{AD}$ is 4.

Find the measure of $\dpi{100} \small \angle ADB$ .

Answer

The measure of $\dpi{100} \small \angle ADB$ is $30^{\circ}$ . Since $\dpi{100} \small A$ , $\dpi{100} \small B$ , and $\dpi{100} \small C$ are collinear, and the measure of $\dpi{100} \small \angle CBD$ is $60^{\circ}$ , we know that the measure of $\dpi{100} \small \angle ABD$ is $120^{\circ}$ .

Because the measures of the three angles in a triangle must add up to $180^{\circ}$ , and two of the angles in triangle $\dpi{100} \small ABD$ are $30^{\circ}$ and $120^{\circ}$ , the third angle, $\dpi{100} \small \angle ADB$ , is $30^{\circ}$ .

Compare your answer with the correct one above

Question

Two interior angles in an obtuse triangle measure $123^{\circ}$ and $11^{\circ}$ . What is the measurement of the third angle.

Answer

Interior angles of a triangle always add up to 180 degrees.

Compare your answer with the correct one above

Question

In a given triangle, the angles are in a ratio of 1:3:5. What size is the middle angle?

Answer

Since the sum of the angles of a triangle is $180^{\circ}$ , and given that the angles are in a ratio of 1:3:5, let the measure of the smallest angle be , then the following expression could be written:

$x+3x+5x=180$

$9x=180$

$x=20$

If the smallest angle is 20 degrees, then given that the middle angle is in ratio of 1:3, the middle angle would be 3 times as large, or 60 degrees.

Compare your answer with the correct one above

Question

Observe the following image and answer the question below:

Are triangles and congruent?

Answer

Two triangles are only congruent if all of their sides are the same length, and all of the corresponding angles are of the same degree. Luckily, we only need three of these six numbers to completely determine the others, as long as we have at least one angle and one side, and any other combination of the other numbers.

In this case, we have two adjacent angles and one side, directly across from one of our angles in both triangles. This can be called the AAS case. We can see from our picture that all of our angles match, and the two sides match as well. They're all in the same position relative to each other on the triangle, so that is enough information to say that the two triangles are congruent.

Compare your answer with the correct one above

Question

The ratio of the side lengths of a triangle is 7:10:11. In a similar triangle, the middle side is 9 inches long. What is the length of the longest side of the second triangle?

Answer

Side lengths of similar triangles can be expressed in proportions. Establish a proportion comparing the middle and long sides of your triangles.

10/11 = 9/x

Cross multiply and solve for x.

10x = 99

x = 9.9

Compare your answer with the correct one above

Question

Two triangles are similar to each other. The bigger one has side lengths of 12, 3, and 14.

The smaller triangle's shortest side is 1 unit in length. What is the length of the smaller triangle's longest side?

Answer

Because the triangles are similar, a ratio can be set up between the triangles' longest sides and shortest sides as such: 14/3 = x/1. Solving for x, we obtain that the shortest side of the triangle is 14/3 units long.

Compare your answer with the correct one above

Question

The ratio of the side lengths of a triangle is . The longest side of a similar triangle is . What is the length of the smallest side of that similar triangle?

Answer

Use proportions to solve for the missing side:

$\frac{20}{24}=\frac{11}x{}$

Cross multiply and solve:

$\frac{264}{20}=x=13.2$

Compare your answer with the correct one above

Question

There are two similar triangles. One has side lengths of 14, 17, and 19. The smaller triangle's smallest side length is 2. What is the length of its longest side?

Answer

Use proportions to solve for the missing side:

$\frac{2}{14}=\frac{x}{19}$

Cross multiply and solve:

$\frac{38}{14}=x=2.7$

Compare your answer with the correct one above

Question

The base of a triangle is $8\ cm$ and the area is $48\ cm^2$ . The height of the triangle is then decreased by 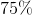. What is the final area of the triangle?

Answer

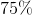
The formula for the area of a triangle is

$\frac{1}{2}b \times h$ .

If the area is equal to 48 cm2 and the base is 8 cm, then the initial height is:

$48 = \frac{1}{2} \times 8 \times h$

If 12 is decreased by 75% then

$12 \times .75 = 9$ , and . The final height is 3 cm.

Therefore the final area is

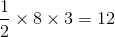$\frac{1}{2}\times 8\times 3=12$ .

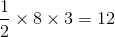
Compare your answer with the correct one above

Question

If the area of an isosceles triangle is and its base is , what is the height of the triangle?

Answer

Use the formula for area of a triangle to solve for the height:

$A=\frac{1}{2}(b)(h)$

$50=\frac{1}{2}(10)(h)$

Compare your answer with the correct one above

Question

Find the height of the isosceles triangle above if the length of $\overline{AB}=12$ and $\overline{BC}=8$ . If your answer is in a decimal form, round to the nearest tenths place.

Answer

Because this is an isosceles triangle, $\overline{AC}=\overline{AB}$ . Also, we know that the base of the triangle, $\overline{BC}=8$ . Therefore, we create two triangles by bisecting the trinagle down the center. We are solving for the length of the long arm of the triangle. We know that the hypotenuse is 12 and the base is 4 (half of 8).

Thus we use the Pythagorean Theorem to find the length of the long arm:

$12^{2} = 4^2+h^2$

$h = \sqrt{12^2-4^2}$

Compare your answer with the correct one above

Question

The triangle above has an area of units squared. If the length of the base is units, what is the height of the triangle?

Answer

The area of a triangle is found using the formula

$A=\frac{1}{2}(base)(height)$

The height of any triangle is the length from it's highest point to the base, as pictured below:

We can find the height by rearranging the area formula:

$h = \frac{2A}{b} = \frac{2(15)}{10} = 3$

Compare your answer with the correct one above

Question

What is the value of in the triangle above? Round to the nearest hundredth.

Answer

Begin by filling in the missing angle for your triangle. Since a triangle has a total of degrees, you know that the missing angle is:

Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:

$\frac{sin(30)}{30}=\frac{sin(100)}{x}$

Solving for , you get:

$x=\frac{30sin(100)}{sin(30)}=59.0884651807326...$

Rounding, this is .

Compare your answer with the correct one above

Question

A triangle has a perimeter of 36 inches, and one side that is 12 inches long. The lengths of the other two sides have a ratio of 3:5. What is the length of the longest side of the triangle?

Answer

We know that the perimeter is 36 inches, and one side is 12. This means, the sum of the lengths of the other two sides are 24. The ratio between the two sides is 3:5, giving a total of 8 parts. We divide the remaining length, 24 inches, by 8 giving us 3. This means each part is 3. We multiply this by the ratio and get 9:15, meaning the longest side is 15 inches.

Compare your answer with the correct one above

Question

What is the value of in the triangle above? Round to the nearest hundredth.

Answer

What is the value of in the triangle above? Round to the nearest hundredth.

Begin by filling in the missing angle for your triangle. Since a triangle has a total of degrees, you know that the missing angle is:

Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:

$\frac{sin(34)}{17}=\frac{sin(135)}{x}$

Solving for , you get:

$x=\frac{34sin(135)}{sin(34)}=42.99344718275794$

Rounding, this is .

Compare your answer with the correct one above

Question

What is the value of in the triangle above? Round to the nearest hundredth.

Answer

Begin by filling in the missing angle for your triangle. Since a triangle has a total of degrees, you know that the missing angle is:

Draw out the figure:

Now, to solve this, you will need some trigonometry. Use the Law of Sines to calculate the value:

$\frac{sin(20)}{7}=\frac{sin(50)}{x}$

Solving for , you get:

$x=\frac{7sin(50)}{sin(20)}=15.67834879458227...$

Rounding, this is .

Compare your answer with the correct one above

Question

What is the length of side ? Round to the nearest hundredth.

Answer

Begin by filling in the missing angle for your triangle. Since a triangle has a total of degrees, you know that the missing angle is:

Draw out the figure:

This problem becomes incredibly easy! This is an isosceles triangle. Therefore, you know that is , because it is "across" from a degree angle—which matches the other degree angle!

Compare your answer with the correct one above

Question

Two similiar triangles exist where the ratio of perimeters is 4:5 for the smaller to the larger triangle. If the larger triangle has sides of 6, 7, and 12 inches, what is the perimeter, in inches, of the smaller triangle?

Answer

The larger triangle has a perimeter of 25 inches. Therefore, using a 4:5 ratio, the smaller triangle's perimeter will be 20 inches.

Compare your answer with the correct one above

Tap the card to reveal the answer