Cubes - ACT Math

Card 0 of 20

Question

Find the length of the diagonal of a cube with side length of .

Answer

We begin with a picture, noting that the diagonal, labeled as , is the length across the cube from one vertex to the opposite side's vertex.

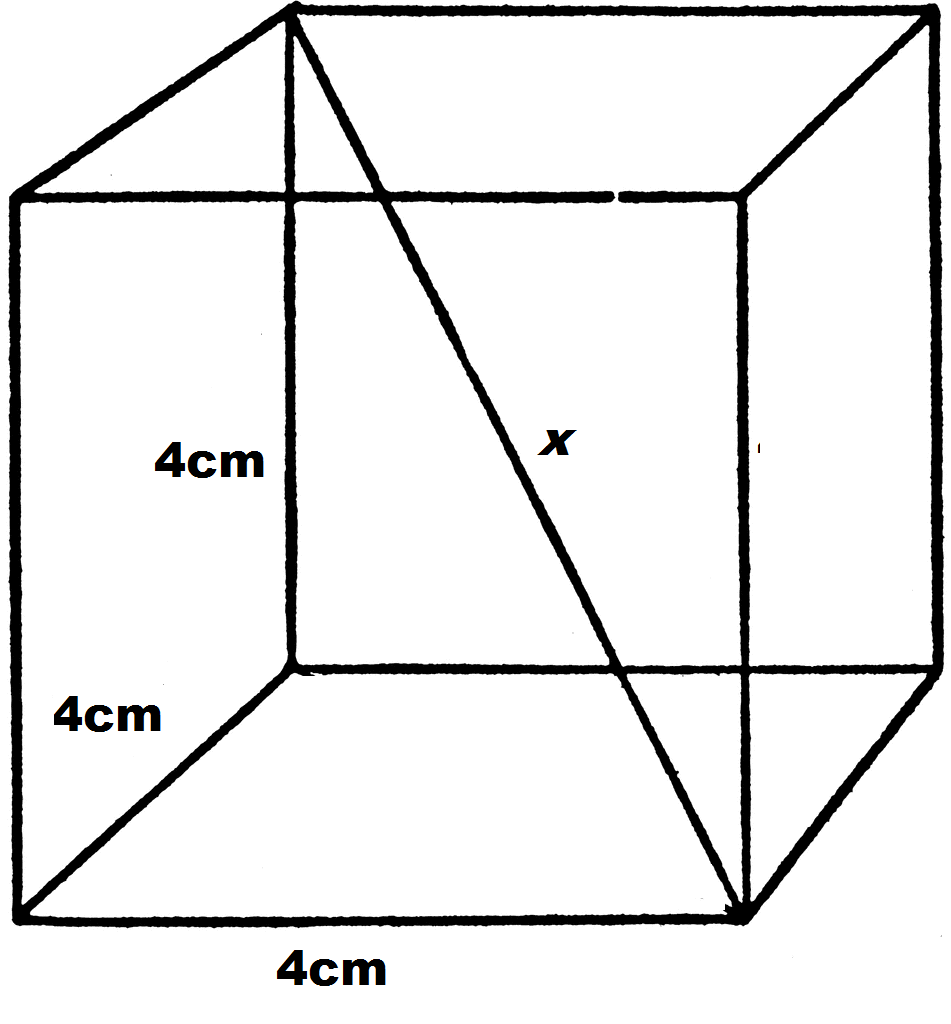
However, the trick to solving the problem is to also draw in the diagonal of the bottom face of the cube, which we labeled .

Note that this creates two right triangles. Though our end goal is to find , we can begin by looking at the right triangle in the bottom face to find . Using either the Pythagorean Theorem or the fact that we have a 45-45-90 right traingle, we can calculate the hypotenuse.

$y=4\sqrt{2}$

Now that we know the value of , we can turn to our second right triangle to find using the Pythagorean Theorem.

$(4)^2+(4\sqrt{2})^2=x^2$

Taking the square root of both sides and simplifying gives the answer.

$x=4\sqrt{3}cm$

Compare your answer with the correct one above

Question

What is the diagonal length for a cube with volume of ? Round to the nearest hundredth.

Answer

Recall that the volume of a cube is computed using the equation

, where is the length of one side of the cube.

So, for our data, we know:

Using your calculator, take the cube root of both sides. You can always do this by raising to the $\frac{1}{3}$ power if your calculator does not have a varied-root button.

$\sqrt[3]{91.125} = \sqrt[3]{s^3}$

If you get , the value really should be rounded up to . This is because of calculator estimations. So, if the sides are , you can find the diagonal by using a variation on the Pythagorean Theorem working for three dimensions:

$diagonal=\sqrt{s^2+s^2+s^2}$

$diagonal = \sqrt{4.5^2+4.5^2+4.5^2}=\sqrt{60.75}$

This is . Round it to .

Compare your answer with the correct one above

Question

What is the length of the diagonal of a cube with a volume of ?

Answer

Recall that the diagonal of a cube is most easily found when you know that cube's dimensions. For the volume of a cube, the pertinent equation is:

, where represents the length of one side of the cube. For our data, this gives us:

Now, you could factor this by hand or use your calculator. You will see that is .

Now, we find the diagonal by using a three-dimensional version of the Pythagorean Theorem / distance formula:

$d = \sqrt{33^2+33^2+33^2}$ or $d=\sqrt{3*33^2}$

You can rewrite this:

$d=33\sqrt{3}$

Compare your answer with the correct one above

Question

Our backyard pool holds 10,000 gallons. Its average depth is 4 feet deep and it is 10 feet long. If there are 7.48 gallons in a cubic foot, how wide is the pool?

Answer

There are 7.48 gallons in cubic foot. Set up a ratio:

1 ft3 / 7.48 gallons = x cubic feet / 10,000 gallons

Pool Volume = 10,000 gallons = 10,000 gallons * (1 ft3/ 7.48 gallons) = 1336.9 ft3

Pool Volume = 4ft x 10 ft x WIDTH = 1336.9 cubic feet

Solve for WIDTH:

4 ft x 10 ft x WIDTH = 1336.9 cubic feet

WIDTH = 1336.9 / (4 x 10) = 33.4 ft

Compare your answer with the correct one above

Question

A cube has a volume of 64cm3. What is the area of one side of the cube?

Answer

The cube has a volume of 64cm3, making the length of one edge 4cm (4 * 4 * 4 = 64).

So the area of one side is 4 * 4 = 16cm2

Compare your answer with the correct one above

Question

A cube as the volume of .

Find the length of a side of this cube.

Answer

The formula to find the volume of the cube is

Since we know the volume, we can set up the equation

$\sqrt[3]64=4$

Compare your answer with the correct one above

Question

A cube has a surface area of $1014\textup{ in}^2$ , what is the length of the side of the cube? (If necessary, round to the nearest hundredth.)

Answer

To find the length of the side of a square given the surface area, use the surface area formula and solve for :

$1014\textup{ inches}^2 = 6*s^2$ , now divide both sides by 6
$169\textup{ inches}^2 = s^2$ , now square root both sides
.

Compare your answer with the correct one above

Question

A certain cubic box when unfolded and laid flat on a table covers exactly square units of space. What is the width of the box, in units?

Answer

To find the length of the edge of a cube from its surface area, remember that $SA\square = 6s^2$ , where is the length of a side.

$s = \sqrt{60} = 2\sqrt{15}$

So, the box is $2\sqrt{15}$ units long.

Compare your answer with the correct one above

Question

Given the volume of a cube is , find the side length.

Answer

To find side length, simply realize that volume is the side length cubed. Thus,

$s=\sqrt[3]{V}=\sqrt[3]{64}=\sqrt[3]{4^3}=4$

Compare your answer with the correct one above

Question

Find the length of the edge of a cube given the volume is .

Answer

To solve, simply take the cube root of the volume. Thus,

$s=\sqrt[3]{V}=\sqrt[3]{27}=3$

Compare your answer with the correct one above

Question

If the surface area of a cube equals 96, what is the length of one side of the cube?

Answer

The surface area of a cube = 6a2 where a is the length of the side of each edge of the cube. Put another way, since all sides of a cube are equal, a is just the lenght of one side of a cube.

We have 96 = 6a2 → a2 = 16, so that's the area of one face of the cube.

Solving we get √16, so a = 4

Compare your answer with the correct one above

Question

A sphere with a volume of $\frac{32}{3}$ $\pi m^{3}$ is inscribed in a cube, as shown in the diagram below.

What is the surface area of the cube, in $m^{2}$ ?

Answer

We must first find the radius of the sphere in order to solve this problem. Since we already know the volume, we will use the volume formula to do this.

$V_{sphere}=\frac{4}{3}\pi r^{3}$

$\frac{32}{3}\pi =\frac{4}{3}\pi r^{3}$

$\frac{32}{3}=\frac{4}{3}r^{3}$

$\frac{3}{4}\cdot \frac{32}{3}= r^{3}$

$8=r^{3}$

With the radius of the sphere in hand, we can now apply it to the cube. The radius of the sphere is half the distance from the top to the bottom of the cube (or half the distance from one side to another). Therefore, the radius represents half of a side length of a square. So in this case

$side=2\cdot 2=4$

The formula for the surface area of a cube is:

$SA_{cube}=6s^{2}$

$6s^{2}=6\cdot (4)^{2}=6\cdot 16=96$

The surface area of the cube is $96\ m^{2}$

Compare your answer with the correct one above

Question

What is the surface area of a cube if its height is 3 cm?

Answer

The area of one face is given by the length of a side squared.

$A_{face}=(3cm)^2=9\ cm^2$

The area of 6 faces is then given by six times the area of one face: 54 cm2.

$A_{total}=6(A_{face})=6(9\ cm^2)=54\ cm^2$

Compare your answer with the correct one above

Question

The side of a cube has a length of $\dpi{100} \small 5 cm$ . What is the total surface area of the cube?

Answer

A cube has 6 faces. The area of each face is found by squaring the length of the side.

$\dpi{100} \small 5\times 5 = 25$

Multiply the area of one face by the number of faces to get the total surface area of the cube.

$\dpi{100} \small 25 \times 6=150$

Compare your answer with the correct one above

Question

What is the surface area, in square inches, of a four-inch cube?

Answer

To answer this question, we need to find the surface area of a cube.

To do this, we must find the area of one face and multiply it by , because a cube has faces that are square in shape and equal in size.

To find the area of a square, you multiply its length by its width. (Note that the length and width of a square are the same.) Therefore, for this data:

$area = L\cdot W=4:in\cdot 4:in=16:in^2$

We now must multiply the area of one face by 6 to get the total surface are of the cube.

$16:in^2\cdot6=96:in^2$

Therefore, the surface are of a four-inch cube is .

Compare your answer with the correct one above

Question

What is the surface area, in square inches, of a cube with sides measuring ?

Answer

The surface area of a cube is a measure of the total area of thesurface of all of the sides of that cube.

Since a cube contains square sides, the surface area is times the area of a square side.

The area of one square side is sidelength sidelength, or in this case. Therefore, the surface area of this cube is square inches.

Compare your answer with the correct one above

Question

What is the surface area of a cube with a volume of ? Round your answer to the nearest hundreth if necessary

Answer

First we need to find the side length of the cube. Do that by taking the cube root of the volume.

$\sqrt[n]{512mm^3}$ =
Next plug the side length into the formula for the surface area of a cube:

Compare your answer with the correct one above

Question

What is the length of the side of a cube whose surface area is equal to its volume?

Answer

To find the side length of a cube whose surface area is the same as its volume, set the surface area and volume equations of a cube equal to each other, the solve for the side length:

Set these two formulas equal to eachother and solve for s.

$\ s^3 = 6s^2 \ ewline \frac{s^3}{s^2}=\frac{6s^2}{s^2}\ ewline s = 6$

Compare your answer with the correct one above

Question

What is the surface area of a cube with a side of length $\textup{3ft}$ ?

Answer

To find the surface area of a cube with a given side length, use the formula:

Compare your answer with the correct one above

Question

Find the surface area of a cube whose side length is .

Answer

To find surface area of a cube, simply calculate the area of one side and multiply it by . Thus,

Compare your answer with the correct one above

Tap the card to reveal the answer