Trapezoids - ACT Math
Card 0 of 16
Find the measure of angle 
in the isosceles trapezoid pictured below.
Find the measure of angle
The sum of the angles in any quadrilateral is 360**°, and the properties of an isosceles trapezoid dictate that the sets of angles adjoined by parallel lines (in this case, the bottom set and top set of angles) are equal. Subtracting 2(72°) from 360°** gives the sum of the two top angles, and dividing the resulting 216**°** by 2 yields the measurement of x, which is 108**°**.
The sum of the angles in any quadrilateral is 360**°, and the properties of an isosceles trapezoid dictate that the sets of angles adjoined by parallel lines (in this case, the bottom set and top set of angles) are equal. Subtracting 2(72°) from 360°** gives the sum of the two top angles, and dividing the resulting 216**°** by 2 yields the measurement of x, which is 108**°**.
Compare your answer with the correct one above
Given the following isosceles triangle:
In degrees, find the measure of the sum of 
and 
in the figure above.
Given the following isosceles triangle:
In degrees, find the measure of the sum of
All quadrilaterals' interior angles sum to 360°. In isosceles trapezoids, the two top angles are equal to each other.
Similarly, the two bottom angles are equal to each other as well.
Therefore, to find the sum of the two bottom angles, we subtract the measures of the top two angles from 360:
All quadrilaterals' interior angles sum to 360°. In isosceles trapezoids, the two top angles are equal to each other.
Similarly, the two bottom angles are equal to each other as well.
Therefore, to find the sum of the two bottom angles, we subtract the measures of the top two angles from 360:
Compare your answer with the correct one above
In the isosceles trapezoid above,
. 
and 
.
In degrees, what is the measure of 
?
In the isosceles trapezoid above,
In degrees, what is the measure of
To find the measure of angle DAC, we must know that the interior angles of all triangles sum up to 180 degrees. Also, as this is an isosceles trapezoid, 
and 
are equal to each other. The two diagonals within the trapezoid bisect angles 
and 
at the same angle.
Thus, 
must also be equal to 50 degrees.
Thus, 
.
Now that we know two angles out of the three in the triangle on the left, we can subtract them from 180 degrees to find 
:
To find the measure of angle DAC, we must know that the interior angles of all triangles sum up to 180 degrees. Also, as this is an isosceles trapezoid,
Thus,
Thus,
Now that we know two angles out of the three in the triangle on the left, we can subtract them from 180 degrees to find
Compare your answer with the correct one above
Trapezoid 
is an isosceles trapezoid with angle 
. If 
and 
are paired, what is the measure of 
?
Trapezoid
As a rule, adjacent (non-paired) angles in a trapezoid are supplementary. Thus, we know that if 
, then 
. Since we are told that 
and 
are paired and trapezoid 
is isosceles, 
must also equal 
.
As a rule, adjacent (non-paired) angles in a trapezoid are supplementary. Thus, we know that if
Compare your answer with the correct one above
Trapezoid A and Trapezoid B are similar. The bases of Trapezoid A are 
and 
. Trapezoid B has a smaller base of 
. How long is the larger base of Trapezoid B?
Trapezoid A and Trapezoid B are similar. The bases of Trapezoid A are
Because the two trapezoids are similar, the ratio of their bases must be the same. Therefore, we must set up a cross-multiplication to solve for the missing base:
, using 
as the variable for the missing base.
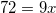
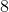
Therefore, the length of the longer base of Trapezoid B is 
.
Because the two trapezoids are similar, the ratio of their bases must be the same. Therefore, we must set up a cross-multiplication to solve for the missing base:
Therefore, the length of the longer base of Trapezoid B is
Compare your answer with the correct one above
Find the area of a trapezoid given bases of length 6 and 7 and height of 2.
Find the area of a trapezoid given bases of length 6 and 7 and height of 2.
To solve, simply use the formula for the area of a trapezoid.
Substitute
into the area formula.
Thus,
To solve, simply use the formula for the area of a trapezoid.
Substitute
into the area formula.
Thus,
Compare your answer with the correct one above
What is the area of this regular trapezoid?
What is the area of this regular trapezoid?
To solve this question, you must divide the trapezoid into a rectangle and two right triangles. Using the Pythagorean Theorem, you would calculate the height of the triangle which is 4. The dimensions of the rectangle are 5 and 4, hence the area will be 20. The base of the triangle is 3 and the height of the triangle is 4. The area of one triangle is 6. Hence the total area will be 20+6+6=32. If you forget to split the shape into a rectangle and TWO triangles, or if you add the dimensions of the trapezoid, you could arrive at 26 as your answer.
To solve this question, you must divide the trapezoid into a rectangle and two right triangles. Using the Pythagorean Theorem, you would calculate the height of the triangle which is 4. The dimensions of the rectangle are 5 and 4, hence the area will be 20. The base of the triangle is 3 and the height of the triangle is 4. The area of one triangle is 6. Hence the total area will be 20+6+6=32. If you forget to split the shape into a rectangle and TWO triangles, or if you add the dimensions of the trapezoid, you could arrive at 26 as your answer.
Compare your answer with the correct one above
What is the area of the trapezoid above if a = 2, b = 6, and h = 4?
What is the area of the trapezoid above if a = 2, b = 6, and h = 4?
Area of a Trapezoid = ½(a+b)*h
= ½ (2+6) * 4
= ½ (8) * 4
= 4 * 4 = 16
Area of a Trapezoid = ½(a+b)*h
= ½ (2+6) * 4
= ½ (8) * 4
= 4 * 4 = 16
Compare your answer with the correct one above
Find the area of a trapezoid if the height is 
, and the small and large bases are 
and 
, respectively.
Find the area of a trapezoid if the height is
Write the formula to find the area of a trapezoid.
Substitute the givens and evaluate the area.
Write the formula to find the area of a trapezoid.
Substitute the givens and evaluate the area.
Compare your answer with the correct one above
Trapezoid 
has an area of 
. If height 
and 
, what is the measure of 
?
Trapezoid
The formula for the area of a trapezoid is:
We have here the height and one of the bases, plus the area, and we are being asked to find the length of base 
. Plug in known values and solve.
Thus, 
The formula for the area of a trapezoid is:
We have here the height and one of the bases, plus the area, and we are being asked to find the length of base
Thus,
Compare your answer with the correct one above
A trapezoid has bases of length 
and 
and side lengths of 
and 
. What is the upper non-inclusive limit of the trapezoid's diagonal length?
A trapezoid has bases of length
The upper limit of a trapezoid's diagonal length is determined by the lengths of the larger base and larger side because the larger base, larger side and longest diagonal form a triangle, meaning you can use a triangle's side length rule.
Specifically, the non-inclusive upper limit will be the sum of the larger base and larger side.
In this case, 
, meaning that the diagonal length can go up to but not including 
.
The upper limit of a trapezoid's diagonal length is determined by the lengths of the larger base and larger side because the larger base, larger side and longest diagonal form a triangle, meaning you can use a triangle's side length rule.
Specifically, the non-inclusive upper limit will be the sum of the larger base and larger side.
In this case,
Compare your answer with the correct one above
If the height of the trapezoid above is 
units, what is the length of the diagonal 
?
If the height of the trapezoid above is
To find the diagonal, we must subtract the top base from the bottom base:
This leaves us with 4, which is the sum of the distance to the left and right of the top base. Taking half of that
gives us the length of the distance to only the left side.
This means that the base of a triangle that includes that diagonal is equal to
.
Since the height is 
, we can solve this problem either using the Pythagorean Theorum or by remembering that this is a special right triangle (
triangle). Therefore, the hypotenuse is 
.
See the figure below for clarification:
To find the diagonal, we must subtract the top base from the bottom base:
This leaves us with 4, which is the sum of the distance to the left and right of the top base. Taking half of that
This means that the base of a triangle that includes that diagonal is equal to
Since the height is
See the figure below for clarification:
Compare your answer with the correct one above
Suppose the lengths of the bases of a trapezoid are 1 and 5 respectively. The altitude of the trapezoid is 4. What is the diagonal of the trapezoid?
Suppose the lengths of the bases of a trapezoid are 1 and 5 respectively. The altitude of the trapezoid is 4. What is the diagonal of the trapezoid?
The altitude of the trapezoid splits the trapezoid into two right triangles and a rectangle. Choose one of those right triangles. The base length of that right triangle is necessary to solve for the diagonal.
Using the base lengths of the trapezoid, the length of the base of the right triangle can be solved. The length of the rectangle is 1 unit. The longer length of the trapezoid base is 5 units.
Since there are 2 right triangles bases that lie on the longer base of the trapezoid, we will assume that their base lengths are 
since their lengths are unknown. Combining the lengths of the right triangles and the rectangle, write the equation to solve for the length of the right triangle bases.
The length of each triangular base is 2.
The diagonal of the trapezoid connects from either bottom angle of the trapezoid to the far upper corner of the rectangle. This diagonal connects to form another right triangle, where the sum of the solved triangular base and the rectangle length is a leg, and the altitude of the trapezoid is another leg.
Use the Pythagorean Theorem to solve for the diagonal.
The altitude of the trapezoid splits the trapezoid into two right triangles and a rectangle. Choose one of those right triangles. The base length of that right triangle is necessary to solve for the diagonal.
Using the base lengths of the trapezoid, the length of the base of the right triangle can be solved. The length of the rectangle is 1 unit. The longer length of the trapezoid base is 5 units.
Since there are 2 right triangles bases that lie on the longer base of the trapezoid, we will assume that their base lengths are
The length of each triangular base is 2.
The diagonal of the trapezoid connects from either bottom angle of the trapezoid to the far upper corner of the rectangle. This diagonal connects to form another right triangle, where the sum of the solved triangular base and the rectangle length is a leg, and the altitude of the trapezoid is another leg.
Use the Pythagorean Theorem to solve for the diagonal.
Compare your answer with the correct one above
Given the height of a trapezoid is 
and a base length is 
, what is the length of the other base if the area of the trapezoid is 
?
Given the height of a trapezoid is
Write the formula used to find the area of a trapezoid.
Substitute the given information to the formula and solve for the unknown base.
Write the formula used to find the area of a trapezoid.
Substitute the given information to the formula and solve for the unknown base.
Compare your answer with the correct one above
is an isosceles trapezoid that is bisected by 
.
. If 
, 
, and 
, then what is the length of 
?
We know that all three horizontal lines are parallel to one another. By definition, we can set up a ratio between the lengths of the sides provided to us in the question and the lengths of the two parallel lines:
Once we substitute the given information, we get
We cross multiply to solve for EF
We know that all three horizontal lines are parallel to one another. By definition, we can set up a ratio between the lengths of the sides provided to us in the question and the lengths of the two parallel lines:
Once we substitute the given information, we get
We cross multiply to solve for EF
Compare your answer with the correct one above
If a trapezoid has a height of 14, base lengths of 10 and 12, and side lengths of 13, what is its perimeter?
If a trapezoid has a height of 14, base lengths of 10 and 12, and side lengths of 13, what is its perimeter?
Use the formula for perimeter of a trapezoid:
Where 
is the perimeter, 
and 
are the lengths of the bases, and 
is the length of the side.
In this case:
Use the formula for perimeter of a trapezoid:
Where
In this case:
Compare your answer with the correct one above