Parallelograms - ACT Math
Card 0 of 20
In the parallellogram, what is the value of  ?
?

In the parallellogram, what is the value of 

Opposite angles are equal, and adjacent angles must sum to 180.
Therefore, we can set up an equation to solve for z:
(z – 15) + 2z = 180
3z - 15 = 180
3z = 195
z = 65
Now solve for x:
2_z_ = x = 130°
Opposite angles are equal, and adjacent angles must sum to 180.
Therefore, we can set up an equation to solve for z:
(z – 15) + 2z = 180
3z - 15 = 180
3z = 195
z = 65
Now solve for x:
2_z_ = x = 130°
Compare your answer with the correct one above

In parallelogram  ,
,  . What is
. What is 

In parallelogram 

In the above parallelogram,  and
and  are consecutive angles (i.e. next to each other). In a parallelogram, consecutive angles are supplementary, meaning they add to
are consecutive angles (i.e. next to each other). In a parallelogram, consecutive angles are supplementary, meaning they add to  .
.



In the above parallelogram, 


Compare your answer with the correct one above

In parallelogram  ,
,  . What is
. What is  ?
?

In parallelogram 


In parallelogram  ,
,  and
and  are opposite angles. In a parallelogram, opposite angles are congruent. This means these two angles are equal.
are opposite angles. In a parallelogram, opposite angles are congruent. This means these two angles are equal.


In parallelogram 


Compare your answer with the correct one above

In parallelogram  ,
,  and the height is
and the height is  . What is
. What is  ?
?

In parallelogram 



We can start this problem by drawing the height and labeling the lengths with the given values.

When we do this, we can see that we have drawn a triangle inside the paralellogram including  . Because we know the lengths of two sides of this triangle, we can use trigonometry to find
. Because we know the lengths of two sides of this triangle, we can use trigonometry to find  .
.
With respect to  , we know the values of the opposite and hypotenuse sides of the triangle. Thus, we can use the sine function to solve for
, we know the values of the opposite and hypotenuse sides of the triangle. Thus, we can use the sine function to solve for  .
.



We can start this problem by drawing the height and labeling the lengths with the given values.

When we do this, we can see that we have drawn a triangle inside the paralellogram including 

With respect to 

Compare your answer with the correct one above

In parallelogram  , what is the sum of
, what is the sum of  and
and  ?
?

In parallelogram 


In a parallelogram, consecutive angles are supplementary.  and
and  are consecutive, so their sum is
are consecutive, so their sum is  .
.
In a parallelogram, consecutive angles are supplementary. 


Compare your answer with the correct one above

In parallelogram  ,
,  and
and  . Find
. Find  .
.

In parallelogram 



In a parallelogram, consecutive angles are supplementary. Thus,





In a parallelogram, consecutive angles are supplementary. Thus,
Compare your answer with the correct one above

 is a parallelogram. Find
is a parallelogram. Find  .
.



In a parallelogram, consecutive angles are supplementary (i.e. add to  ) and opposite angles are congruent (i.e. equal). Using these properties, we can write a system of equations.
) and opposite angles are congruent (i.e. equal). Using these properties, we can write a system of equations.
1. 
2. 
Starting with equation 1.,



Now substituting into equation 2.,





Finally, because opposite angles are congruent, we know that  .
.


In a parallelogram, consecutive angles are supplementary (i.e. add to 
1.
2.
Starting with equation 1.,
Now substituting into equation 2.,
Finally, because opposite angles are congruent, we know that 
Compare your answer with the correct one above

 is a parallelogram. Find
is a parallelogram. Find  .
.



In a parallelogram, consecutive angles are supplementary and opposite angles are congruent. Using these properties, we can write a system of equations. Because we have three variables, we will need three equations.
1. 
2. 
3. 
Start with equation 1.


Now simplify equation 2.


Finally, simplify equation 3.




Note that we can plug this simplified equation 3 directly into the simplified equation 2 to solve for  .
.

Now that we have  , we can solve for
, we can solve for  using equation 1.
using equation 1.




With  , we can solve for
, we can solve for  using equation 3.
using equation 3.



Now that we have  and
and  , we can solve for
, we can solve for  .
.

In a parallelogram, consecutive angles are supplementary and opposite angles are congruent. Using these properties, we can write a system of equations. Because we have three variables, we will need three equations.
1.
2.
3.
Start with equation 1.
Now simplify equation 2.
Finally, simplify equation 3.
Note that we can plug this simplified equation 3 directly into the simplified equation 2 to solve for 
Now that we have 

With 

Now that we have 


Compare your answer with the correct one above

 is a parallelogram. Find
is a parallelogram. Find  .
.



In a parallelogram, consecutive angles are supplementary and opposite angles are congruent. Using these properties, we can write a system of equations.
1. 
2. 
3. 
Starting with equation 1.,



Substituting into equation 2.,




Using equation 3.,


In a parallelogram, consecutive angles are supplementary and opposite angles are congruent. Using these properties, we can write a system of equations.
1.
2.
3.
Starting with equation 1.,
Substituting into equation 2.,
Using equation 3.,
Compare your answer with the correct one above

In parallelogram  ,
,  . What is
. What is  ?
?

In parallelogram 


In a parellelogram, consecutive angles are supplementary.



In a parellelogram, consecutive angles are supplementary.
Compare your answer with the correct one above

In parallelogram  ,
,  . What is
. What is  ?
?

In parallelogram 


In a parallelogram, opposite angles are congruent.


In a parallelogram, opposite angles are congruent.
Compare your answer with the correct one above

 is a parallelogram. Find
is a parallelogram. Find  .
.



In a parallelogram, consecutive angles are supplementary and opposite angles are congruent.








In a parallelogram, consecutive angles are supplementary and opposite angles are congruent.
Compare your answer with the correct one above

 is a parallelogram. Find
is a parallelogram. Find  .
.



In a parallelogram, consecutive angles are supplementary and opposite angles are congruent.









In a parallelogram, consecutive angles are supplementary and opposite angles are congruent.
Compare your answer with the correct one above
In parallelogram  , the length of
, the length of  is
is  units, the length of
units, the length of  is
is  units, and the length of
units, and the length of  is
is  units.
units.  is perpendicular fo
is perpendicular fo  . Find the area, in square units, of
. Find the area, in square units, of  .
.

In parallelogram 










The formula to find the area of a parallelogram is

The base,  , is given by the question.
, is given by the question.


You should recognize that  is not only the height of parallelogram
is not only the height of parallelogram  , but it is also a leg of the right triangle
, but it is also a leg of the right triangle  .
.
Use the Pythagorean Theorem to find the length of  .
.




Now that we have the height, multiply it by the base to find the area of the parallelogram.
The formula to find the area of a parallelogram is
The base, 
You should recognize that 


Use the Pythagorean Theorem to find the length of 
Now that we have the height, multiply it by the base to find the area of the parallelogram.
Compare your answer with the correct one above
A parallelogram has a base of  and its side is
and its side is  long. A line is drawn to connect the edge of the top base with the bottom base. The line is perpendicular to the bottom base, and the base of this triangle is one-fourth the length of the bottom base. Find the area of the parallelogram.
long. A line is drawn to connect the edge of the top base with the bottom base. The line is perpendicular to the bottom base, and the base of this triangle is one-fourth the length of the bottom base. Find the area of the parallelogram.
A parallelogram has a base of 

The formula for the area of a parallelogram is given by the equation  , where
, where  is the base and
is the base and  is the height of the parallelogram.
is the height of the parallelogram.
The only given information is that the base is  , the side is
, the side is  , and the base of the right triangle in the parallelogram (the triangle formed between the edge of the top base and the bottom base) is
, and the base of the right triangle in the parallelogram (the triangle formed between the edge of the top base and the bottom base) is  because
because  .
.
The last part of information that is required to fulfill the needs of the area formula is the parallelogram's height,  . The parallelogram's height is given by the mystery side of the right triangle described in the question. In order to solve for the triangle's third side, we can use the Pythagorean Theorem,
. The parallelogram's height is given by the mystery side of the right triangle described in the question. In order to solve for the triangle's third side, we can use the Pythagorean Theorem,  .
.
In this case, the unknown side is one of the legs of the triangle, so we will label it  . The given side of the triangle that is part of the base we will call
. The given side of the triangle that is part of the base we will call  , and the side of the parallelogram is also the hypotenuse of the triangle, so in the Pythagorean Formula its length will be represented by
, and the side of the parallelogram is also the hypotenuse of the triangle, so in the Pythagorean Formula its length will be represented by  . At this point, we can substitute in these values and solve for
. At this point, we can substitute in these values and solve for  :
:





 , but because we're finding a length, the answer must be 4. The negative option can be negated.
, but because we're finding a length, the answer must be 4. The negative option can be negated.
Remembering that we temporarily called  "
" " for the pythagorean theorem, this means that
" for the pythagorean theorem, this means that  .
.
Now all the necessary parts for the area of a parallelogram equation are available to be used:


The formula for the area of a parallelogram is given by the equation 


The only given information is that the base is 



The last part of information that is required to fulfill the needs of the area formula is the parallelogram's height, 

In this case, the unknown side is one of the legs of the triangle, so we will label it 




Remembering that we temporarily called 


Now all the necessary parts for the area of a parallelogram equation are available to be used:
Compare your answer with the correct one above
If a rectangular plot measures  by
by  , what is the length of the diagonal of the plot, in feet?
, what is the length of the diagonal of the plot, in feet?
If a rectangular plot measures 

To answer this question, we must find the diagonal of a rectangle that is  by
by  . Because a rectangle is made up of right angles, the diagonal of a rectangle creates a right triangle with two of the sides.
. Because a rectangle is made up of right angles, the diagonal of a rectangle creates a right triangle with two of the sides.
Because a right triangle is formed by the diagonal, we can use the Pythagorean Theorem, which is:

 and
and  each represent a different leg of the triangle and
each represent a different leg of the triangle and  represents the length of the hypotenuse, which in this case is the same as the diagonal length.
represents the length of the hypotenuse, which in this case is the same as the diagonal length.
We can then plug in our known values and solve for 

We now must take the square root of each side so that we can solve for 

Therefore, the diagonal of the rectangle is  .
.
To answer this question, we must find the diagonal of a rectangle that is 

Because a right triangle is formed by the diagonal, we can use the Pythagorean Theorem, which is:



We can then plug in our known values and solve for
We now must take the square root of each side so that we can solve for
Therefore, the diagonal of the rectangle is 
Compare your answer with the correct one above
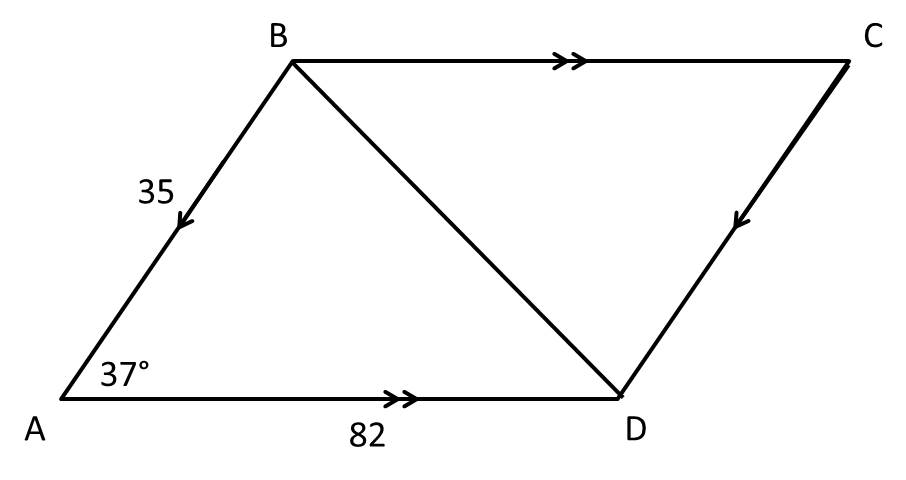
 is a parallelogram. Find the length of diagonal
is a parallelogram. Find the length of diagonal  .
.



To find the length of the diagonal, we can consider only the triangle  and use the law of cosines to find the length of the unknown side.
and use the law of cosines to find the length of the unknown side.
The Law of Cosines:

Where  is the length of the unknown side,
is the length of the unknown side,  and
and  are the lengths of the known sides, and
are the lengths of the known sides, and  is the angle between
is the angle between  and
and  .
.
From the problem:




To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
Compare your answer with the correct one above

 is a parallelogram. Find the length of diagonal
is a parallelogram. Find the length of diagonal  .
.



To find the length of the diagonal, we can consider only the triangle  and use the law of cosines to find the length of the unknown side.
and use the law of cosines to find the length of the unknown side.
The Law of Cosines:

Where  is the length of the unknown side,
is the length of the unknown side,  and
and  are the lengths of the known sides, and
are the lengths of the known sides, and  is the angle between
is the angle between  and
and  .
.
From the problem:




To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
Compare your answer with the correct one above

 is a parallelogram. Find the length of diagonal.
is a parallelogram. Find the length of diagonal.  .
.



To find the length of the diagonal, we can consider only the triangle  and use the law of cosines to find the length of the unknown side.
and use the law of cosines to find the length of the unknown side.
The Law of Cosines:

Where  is the length of the unknown side,
is the length of the unknown side,  and
and  are the lengths of the known sides, and
are the lengths of the known sides, and  is the angle between
is the angle between  and
and  .
.
From the problem:




To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
Compare your answer with the correct one above

 is a parallelogram. Find the length of diagonal
is a parallelogram. Find the length of diagonal  .
.



To find the length of the diagonal, we can consider only the triangle  and use the law of cosines to find the length of the unknown side.
and use the law of cosines to find the length of the unknown side.
The Law of Cosines:

Where  is the length of the unknown side,
is the length of the unknown side,  and
and  are the lengths of the known sides, and
are the lengths of the known sides, and  is the angle between
is the angle between  and
and  .
.
From the problem:




To find the length of the diagonal, we can consider only the triangle 
The Law of Cosines:
Where 





From the problem:
Compare your answer with the correct one above