Other Quadrilaterals - ACT Math
Card 0 of 18
The interior angles of a quadrilateral are 
, 
, 
, and 
. What is the measure of the smallest angle of the quadrilateral?
The interior angles of a quadrilateral are 
In order to solve this problem we need the following key piece of knowledge: the interior angles of a quadrilateral add up to 360 degrees. Now, we can write the following equation:
When we combine like terms, we get the following:
We will need to subtract 71 from both sides of the equation:
Now, we will divide both sides of the equation by 17.
We now have a value for the x-variable; however, the problem is not finished. The question asks for the measure of the smallest angle. We know that the smallest angle will be one of the following:
or 
In order to find out, we will substitute 17 degrees for the x-variable.
Because 51 degrees is less than 71 degrees, the measure of the smallest angle is the following:
In order to solve this problem we need the following key piece of knowledge: the interior angles of a quadrilateral add up to 360 degrees. Now, we can write the following equation:
When we combine like terms, we get the following:
We will need to subtract 71 from both sides of the equation:
Now, we will divide both sides of the equation by 17.
We now have a value for the x-variable; however, the problem is not finished. The question asks for the measure of the smallest angle. We know that the smallest angle will be one of the following:
In order to find out, we will substitute 17 degrees for the x-variable.
Because 51 degrees is less than 71 degrees, the measure of the smallest angle is the following:
Compare your answer with the correct one above
bisects 
. If 
then, in degrees, what is the value of 
?
A rectangle has two sets of parallel sides with all angles equaling 90 degrees.
Since 
bisects 
into two equal parts, this creates an isosceles triangle 
.
Therefore 
. The sum of the angles in a triangle is 180 degrees.
Therefore 
A rectangle has two sets of parallel sides with all angles equaling 90 degrees.
Since
Therefore
Therefore
Compare your answer with the correct one above
The rhombus above is bisected by two diagonals.
If 
and 
then, in degrees, what is the value of the 
?
Note: The shape above may not be drawn to scale.
The rhombus above is bisected by two diagonals.
If
Note: The shape above may not be drawn to scale.
A rhombus is a quadrilateral with two sets of parallel sides as well as equal opposite angles. Since the lines drawn inside the rhombus are diagonals, 
and 
are each bisected into two equal angles.
Therefore, 
, which creates a triangle in the upper right quadrant of the kite. The sum of angles in a triangle is 180 degreees.
Thus,
Since 
is only half of 
,
A rhombus is a quadrilateral with two sets of parallel sides as well as equal opposite angles. Since the lines drawn inside the rhombus are diagonals,
Therefore,
Thus,
Since
Compare your answer with the correct one above
If 
and 
, then, in degrees, what is the value of 
?
Note: The figure may not be drawn to scale.
If
Note: The figure may not be drawn to scale.
In a rhombus, opposite angles are equal to each other. Therefore we can set 
and 
equal to one another and solve for 
:
Therefore, 
A rhombus, like any other quadrilateral, has a sum of angles of 360 degrees.
In a rhombus, opposite angles are equal to each other. Therefore we can set
Therefore,
A rhombus, like any other quadrilateral, has a sum of angles of 360 degrees.
Compare your answer with the correct one above
The sides of rectangle A measure to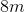 
, 
, 
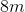, and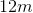 
. Rectangle B is similar to Rectangle A. The shorter sides of rectangle B measure 
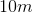each. How long are the longer sides of Rectangle B?
The sides of rectangle A measure to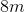
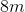
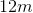
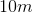
In similar rectangles, the ratio of the sides must be equal.
To solve this question, the following equation must be set up:
, using 
as the variable for the missing side.
We then must cross multiply, which leaves us with:
Lastly, we divide both sides by 8 to solve for the missing side:
Therefore, the longer sides of the rectangle are each 
.
In similar rectangles, the ratio of the sides must be equal.
To solve this question, the following equation must be set up:
We then must cross multiply, which leaves us with:
Lastly, we divide both sides by 8 to solve for the missing side:
Therefore, the longer sides of the rectangle are each
Compare your answer with the correct one above
Suppose a rectangle has side lengths of 7 and 3. Another rectangle has another set of side lengths that are 8 and 4. Are these similar rectangles, and why?
Suppose a rectangle has side lengths of 7 and 3. Another rectangle has another set of side lengths that are 8 and 4. Are these similar rectangles, and why?
Set up the proportion to determine if the ratios of both rectangles are equal.
If they are, then they are similar.
These are not similar rectangles since their ratios are not the same.
Set up the proportion to determine if the ratios of both rectangles are equal.
If they are, then they are similar.
These are not similar rectangles since their ratios are not the same.
Compare your answer with the correct one above
Jane plans to re-tile her kitchen with tiles that have a length of 
inches and a width of 
inches wide. If her kitchen measures 
feet by 
feet, how many tiles will she need?
Jane plans to re-tile her kitchen with tiles that have a length of
When attempting to solve how many pieces of a particular object you need to cover a certain area, always make sure that your units of measurement (for the object and for the area you are covering) are the same. In the case of this question, the units of measurement are different, so you must first convert all measurements to use the same unit.
Since the tiles being used to cover the area are measured in inches, convert all units given to inches:
Length: 
feet 
inches
Width: 
feet 
inches
Then, find the area of the entire space you are covering. Since the space is rectangular (this can be assumed since only length and width are given as measurements), multiply the length and width to find the total area: 
square inches.
Next, find the area of each of the tiles: 
square inches. Divide the total area of the space by the area of each of your tiles: 
. In cases where you are covering a certain area with an object, always round up if you have a decimal (no matter how small), because you cannot simply buy 
of a tile.
The answer is 
.
When attempting to solve how many pieces of a particular object you need to cover a certain area, always make sure that your units of measurement (for the object and for the area you are covering) are the same. In the case of this question, the units of measurement are different, so you must first convert all measurements to use the same unit.
Since the tiles being used to cover the area are measured in inches, convert all units given to inches:
Length:
Width:
Then, find the area of the entire space you are covering. Since the space is rectangular (this can be assumed since only length and width are given as measurements), multiply the length and width to find the total area:
Next, find the area of each of the tiles:
The answer is
Compare your answer with the correct one above
Vikram is looking at a scale drawing of a room he is building. The drawing is of a rectangle that measures 
inches by 
inches. If he knows the length of the longer side of the room will measure 
feet, what is the area of the room?
Vikram is looking at a scale drawing of a room he is building. The drawing is of a rectangle that measures
When solving such problems, always make sure that your units of measurement are all the same. In the case of this problem, you must convert feet to inches. Multiply 30 by 12 in order to get its equivalent in inches.
We know that the 30 feet corresponds with the side of the drawing that is 18 inches because it is stated that the longest side will be 30 feet. Divide 360 by 18 in order to find the ratio of the actual size of the room to the measurements on the drawing
This means that the actual measurements of the room are 20 times the measurements of the drawing. Multiply 20 times 12 in order to find the measurement of the shorter side in inches.
Divide both the 360 and 240 by 12 to convert the measurements back into feet.
Then multiply the results to get the final answer.
When solving such problems, always make sure that your units of measurement are all the same. In the case of this problem, you must convert feet to inches. Multiply 30 by 12 in order to get its equivalent in inches.
We know that the 30 feet corresponds with the side of the drawing that is 18 inches because it is stated that the longest side will be 30 feet. Divide 360 by 18 in order to find the ratio of the actual size of the room to the measurements on the drawing
This means that the actual measurements of the room are 20 times the measurements of the drawing. Multiply 20 times 12 in order to find the measurement of the shorter side in inches.
Divide both the 360 and 240 by 12 to convert the measurements back into feet.
Then multiply the results to get the final answer.
Compare your answer with the correct one above
If a trapezoid has base lengths of 
and 
and a height of 
, what is its area?
If a trapezoid has base lengths of
Use the formula for area of a trapezoid:
Where 
is the area, 
and 
are the lengths of the two bases, and 
is the height.
In this case:
Use the formula for area of a trapezoid:
Where
In this case:
Compare your answer with the correct one above
A parallelogram has a side length of 
, a height of 
, and a base length of 
. What is its area?
A parallelogram has a side length of
Use the formula for area of a parallelogram:
Where 
is the area, 
is the base length, and 
is the height.
In this case:
Use the formula for area of a parallelogram:
Where
In this case:
Compare your answer with the correct one above
In the parallelogram above, 
and 
. What is the length of the diagonal 
?
In the parallelogram above,
In a parallelogram, the two diagonals bisect each other at their centers. Therefore, 
. To find 
, we set them equal to one another and solve.
Plugging this value back into both equations, then adding those values together, gives us our answer of 
.
In a parallelogram, the two diagonals bisect each other at their centers. Therefore,
Plugging this value back into both equations, then adding those values together, gives us our answer of
Compare your answer with the correct one above
A square has a length of 
. What must be the length of the diagonal?
A square has a length of
A square with a length of 
indicates that all sides are 
since a square has 4 equal sides. Use the Pythagorean Theorem to solve for the diagonal.
A square with a length of
Compare your answer with the correct one above
If the rectangle has side lengths of 
and 
, what is the diagonal of the rectangle?
If the rectangle has side lengths of
Use the Pythagorean Theorem to solve for the diagonal.
Use the Pythagorean Theorem to solve for the diagonal.
Compare your answer with the correct one above
Find the perimeter of the rhombus above.
Find the perimeter of the rhombus above.
By definition, a rhombus is a quadrilateral with four equal sides whose angles do not all equal 90 degrees. To find the perimeter, we must find the values of x and y. In order to do so, we must set up a system of equations where we set two sides equal to each other. Any two sides can be used to create these systems.
Here is one example:
Eq. 1
Eq. 2
Now we plug 
into the first equation to find the value of 
:
Plugging these values into any of the three equations will give us the length of one side equaling 11.
Since there are four sides, 
.
By definition, a rhombus is a quadrilateral with four equal sides whose angles do not all equal 90 degrees. To find the perimeter, we must find the values of x and y. In order to do so, we must set up a system of equations where we set two sides equal to each other. Any two sides can be used to create these systems.
Here is one example:
Eq. 1
Eq. 2
Now we plug
Plugging these values into any of the three equations will give us the length of one side equaling 11.
Since there are four sides,
Compare your answer with the correct one above
Find the length of a rectangle if the area is 
, and the width is 
.
Find the length of a rectangle if the area is
Write the formula to solve the area of a rectangle.
Substitute the dimension and area to solve for the length.
Write the formula to solve the area of a rectangle.
Substitute the dimension and area to solve for the length.
Compare your answer with the correct one above
If the perimeter of a square is 
and the area is 
, what is the side length of the square?
If the perimeter of a square is
The square has 4 equal sides. Let's assume a side is 
.
Each side of the square has a length of 
.
The area of the square is:
Substitute 
into the area to solve for 
.
Since one side of the square is 
, substitute the value of 
to determine the length of the square side.
The square has 4 equal sides. Let's assume a side is
Each side of the square has a length of
The area of the square is:
Substitute
Since one side of the square is
Compare your answer with the correct one above
Find the side of a square if the area is 
.
Find the side of a square if the area is
The area of a square is:
Substitute the area and solve for the side.
The quantity inside the square root may not be factorized in attempt to eliminate the square root!
The side length of the square is:
The area of a square is:
Substitute the area and solve for the side.
The quantity inside the square root may not be factorized in attempt to eliminate the square root!
The side length of the square is:
Compare your answer with the correct one above
A homeowner wants to set up a rectangular enclosure for his dog. The plot of land that the enclosure will enclose measures 
by 
. What is the length in feet of chain link fence the owner will need to create a fence around the enclosure?
A homeowner wants to set up a rectangular enclosure for his dog. The plot of land that the enclosure will enclose measures
To answer this question, we must find the perimeter of the fence the homeowner is wanting to create.
To find the perimeter of a rectangle, we multiply the length by two, multiply the width by two, and add these two numbers together. The equation can be represented as this:
We must then plug in our values of 
and 
given to us for the length and width.
So for this data:
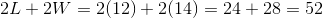
Therefore, the amount of fencing needed to fully surround the dog's enclosure is 
.
To answer this question, we must find the perimeter of the fence the homeowner is wanting to create.
To find the perimeter of a rectangle, we multiply the length by two, multiply the width by two, and add these two numbers together. The equation can be represented as this:
We must then plug in our values of
So for this data:
Therefore, the amount of fencing needed to fully surround the dog's enclosure is
Compare your answer with the correct one above