Hexagons - ACT Math
Card 0 of 20
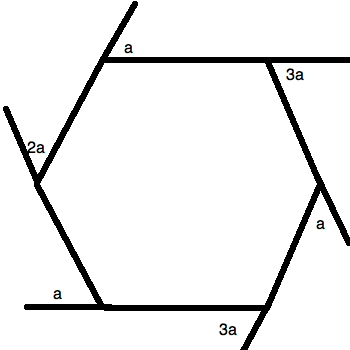
All of the angles marked are exterior angles.
What is the value of  in degrees? Round to the nearest hundredth.
in degrees? Round to the nearest hundredth.

All of the angles marked are exterior angles.
What is the value of 
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:
 , where
, where  is the number of sides.
is the number of sides.
Therefore, a hexagon like this one has:
 .
.
Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:

Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to  . Since there are
. Since there are  angles, you know that the numeric portion will be
angles, you know that the numeric portion will be  or
or  . Thus, you can write:
. Thus, you can write:

Simplify and solve for  :
:



This is  or
or  .
.
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:


Therefore, a hexagon like this one has:

Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:

Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to 



Simplify and solve for 
This is 

Compare your answer with the correct one above
The sum of all the angles inside of a regular hexagon is  . Determine the value of one angle.
. Determine the value of one angle.
The sum of all the angles inside of a regular hexagon is 
In a regular hexagon, all of the sides are the same length, and all of the angles are equivalent. The problem tells us that all of the angles inside the hexagon sum to  . To find the value of one angle, we must divide
. To find the value of one angle, we must divide  by
by  , since there are
, since there are  angles inside of a hexagon.
angles inside of a hexagon.

In a regular hexagon, all of the sides are the same length, and all of the angles are equivalent. The problem tells us that all of the angles inside the hexagon sum to 



Compare your answer with the correct one above

The figure above is a hexagon. All of the angles listed (except the interior one) are exterior angles to the hexagon's interior angles.
What is the value of  ?
?

The figure above is a hexagon. All of the angles listed (except the interior one) are exterior angles to the hexagon's interior angles.
What is the value of 
There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:
 , where
, where  is the number of sides.
is the number of sides.
Therefore, a hexagon like this one has:
 .
.
Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:

Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to  . Thus, you can write:
. Thus, you can write:

Solve for  :
:


There are two key things for a question like this. The first is to know that a polygon has a total degree measure of:


Therefore, a hexagon like this one has:

Next, you should remember that all of the exterior angles listed are supplementary to their correlative interior angles. This lets you draw the following figure:

Now, you just have to manage your algebra well. You must sum up all of the interior angles and set them equal to 
Solve for 
Compare your answer with the correct one above
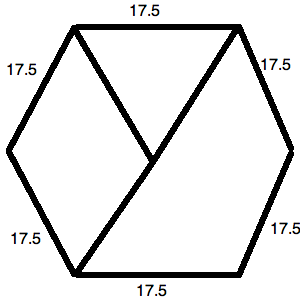
Two hexagons are similar. If they have the ratio of 4:5, and the side of the first hexagon is 16, what is the side of the second hexagon?
Two hexagons are similar. If they have the ratio of 4:5, and the side of the first hexagon is 16, what is the side of the second hexagon?
This type of problem can be solved through using the formula:

If the ratio of the hexagons is 4:5, then  and
and  .
.  denotes area. The side length of the first hexagon is 16.
denotes area. The side length of the first hexagon is 16.
Substituting in the numbers, the formula looks like:

This quickly begins a problem where the second area can be solved for by rearranging all the given information.



The radical can then by simplified with or without a calculator.
Without a calculator, the 320 can be factored out and simplified:


This type of problem can be solved through using the formula:
If the ratio of the hexagons is 4:5, then 


Substituting in the numbers, the formula looks like:
This quickly begins a problem where the second area can be solved for by rearranging all the given information.
The radical can then by simplified with or without a calculator.
Without a calculator, the 320 can be factored out and simplified:
Compare your answer with the correct one above
The ratio between two similar hexagons is  . The side length of the first hexagon is 12 and the second is 17. What must
. The side length of the first hexagon is 12 and the second is 17. What must  be?
be?
The ratio between two similar hexagons is 

This kind of problem can be solved for by using the formula:

where the  values are the similarity ratio and the
values are the similarity ratio and the  values are the side lengths.
values are the side lengths.
In this case, the problem provides  , but not
, but not  .
.  is denoted as
is denoted as  in the question.
in the question.
There are four variables in this formula, and three of them are provided in the problem. This means that we can solve for  (
( ) by substituting in all known values and rearranging the formula so it's in terms of
) by substituting in all known values and rearranging the formula so it's in terms of  .
.



This kind of problem can be solved for by using the formula:
where the 

In this case, the problem provides 



There are four variables in this formula, and three of them are provided in the problem. This means that we can solve for 


Compare your answer with the correct one above
A single hexagonal cell of a honeycomb is two centimeters in diameter.

What’s the area of the cell to the nearest tenth of a centimeter?
A single hexagonal cell of a honeycomb is two centimeters in diameter.

What’s the area of the cell to the nearest tenth of a centimeter?
How do you find the area of a hexagon?
There are several ways to find the area of a hexagon.
- In a regular hexagon, split the figure into triangles.
- Find the area of one triangle.
- Multiply this value by six.
Alternatively, the area can be found by calculating one-half of the side length times the apothem.
Regular hexagons:
Regular hexagons are interesting polygons. Hexagons are six sided figures and possess the following shape:
In a regular hexagon, all sides equal the same length and all interior angles have the same measure; therefore, we can write the following expression.

One of the easiest methods that can be used to find the area of a polygon is to split the figure into triangles. Let's start by splitting the hexagon into six triangles.

In this figure, the center point,  , is equidistant from all of the vertices. As a result, the six dotted lines within the hexagon are the same length. Likewise, all of the triangles within the hexagon are congruent by the side-side-side rule: each of the triangle's share two sides inside the hexagon as well as a base side that makes up the perimeter of the hexagon. In a similar fashion, each of the triangles have the same angles. There are
, is equidistant from all of the vertices. As a result, the six dotted lines within the hexagon are the same length. Likewise, all of the triangles within the hexagon are congruent by the side-side-side rule: each of the triangle's share two sides inside the hexagon as well as a base side that makes up the perimeter of the hexagon. In a similar fashion, each of the triangles have the same angles. There are  in a circle and the hexagon in our image has separated it into six equal parts; therefore, we can write the following:
in a circle and the hexagon in our image has separated it into six equal parts; therefore, we can write the following:



We also know the following:

Now, let's look at each of the triangles in the hexagon. We know that each triangle has two two sides that are equal; therefore, each of the base angles of each triangle must be the same. We know that a triangle has  and we can solve for the two base angles of each triangle using this information.
and we can solve for the two base angles of each triangle using this information.



Each angle in the triangle equals  . We now know that all the triangles are congruent and equilateral: each triangle has three equal side lengths and three equal angles. Now, we can use this vital information to solve for the hexagon's area. If we find the area of one of the triangles, then we can multiply it by six in order to calculate the area of the entire figure. Let's start by analyzing
. We now know that all the triangles are congruent and equilateral: each triangle has three equal side lengths and three equal angles. Now, we can use this vital information to solve for the hexagon's area. If we find the area of one of the triangles, then we can multiply it by six in order to calculate the area of the entire figure. Let's start by analyzing  . If we draw, an altitude through the triangle, then we find that we create two
. If we draw, an altitude through the triangle, then we find that we create two  triangles.
triangles.

Let's solve for the length of this triangle. Remember that in  triangles, triangles possess side lengths in the following ratio:
triangles, triangles possess side lengths in the following ratio:

Now, we can analyze  using the a substitute variable for side length,
using the a substitute variable for side length,  .
.

We know the measure of both the base and height of  and we can solve for its area.
and we can solve for its area.



Now, we need to multiply this by six in order to find the area of the entire hexagon.
![\textup{Area of Hexagon}[ABCDEF]=6\times\frac{\sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065143/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{6 \sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065144/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{3\sqrt{3}}{2}\times s^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065145/gif.latex)
We have solved for the area of a regular hexagon with side length,  . If we know the side length of a regular hexagon, then we can solve for the area.
. If we know the side length of a regular hexagon, then we can solve for the area.
If we are not given a regular hexagon, then we an solve for the area of the hexagon by using the side length(i.e.  ) and apothem (i.e.
) and apothem (i.e.  ), which is the length of a line drawn from the center of the polygon to the right angle of any side. This is denoted by the variable
), which is the length of a line drawn from the center of the polygon to the right angle of any side. This is denoted by the variable  in the following figure:
in the following figure:

Alternative method:
If we are given the variables  and
and  , then we can solve for the area of the hexagon through the following formula:
, then we can solve for the area of the hexagon through the following formula:

In this equation,  is the area,
is the area,  is the perimeter, and
is the perimeter, and  is the apothem. We must calculate the perimeter using the side length and the equation
is the apothem. We must calculate the perimeter using the side length and the equation  , where
, where  is the side length.
is the side length.
Solution:
In the problem we are told that the honeycomb is two centimeters in diameter. In order to solve the problem we need to divide the diameter by two. This is because the radius of this diameter equals the interior side length of the equilateral triangles in the honeycomb. Lets find the side length of the regular hexagon/honeycomb.

Substitute and solve.



We know the following information.

As a result, we can write the following:

Let's substitute this value into the area formula for a regular hexagon and solve.


Simplify.

Solve.

Round to the nearest tenth of a centimeter.

How do you find the area of a hexagon?
There are several ways to find the area of a hexagon.
- In a regular hexagon, split the figure into triangles.
- Find the area of one triangle.
- Multiply this value by six.
Alternatively, the area can be found by calculating one-half of the side length times the apothem.
Regular hexagons:
Regular hexagons are interesting polygons. Hexagons are six sided figures and possess the following shape:
In a regular hexagon, all sides equal the same length and all interior angles have the same measure; therefore, we can write the following expression.
One of the easiest methods that can be used to find the area of a polygon is to split the figure into triangles. Let's start by splitting the hexagon into six triangles.

In this figure, the center point, 


We also know the following:
Now, let's look at each of the triangles in the hexagon. We know that each triangle has two two sides that are equal; therefore, each of the base angles of each triangle must be the same. We know that a triangle has 
Each angle in the triangle equals 



Let's solve for the length of this triangle. Remember that in 
Now, we can analyze 


We know the measure of both the base and height of 
Now, we need to multiply this by six in order to find the area of the entire hexagon.
We have solved for the area of a regular hexagon with side length, 
If we are not given a regular hexagon, then we an solve for the area of the hexagon by using the side length(i.e. 



Alternative method:
If we are given the variables 

In this equation, 




Solution:
In the problem we are told that the honeycomb is two centimeters in diameter. In order to solve the problem we need to divide the diameter by two. This is because the radius of this diameter equals the interior side length of the equilateral triangles in the honeycomb. Lets find the side length of the regular hexagon/honeycomb.
Substitute and solve.
We know the following information.
As a result, we can write the following:
Let's substitute this value into the area formula for a regular hexagon and solve.
Simplify.
Solve.
Round to the nearest tenth of a centimeter.
Compare your answer with the correct one above
A hexagon is made up of 6 congruent equilateral triangles. Each equilateral triangle has a length of 8 units. What is the area in square units of the hexagon?
A hexagon is made up of 6 congruent equilateral triangles. Each equilateral triangle has a length of 8 units. What is the area in square units of the hexagon?
First, let's draw out the hexagon.

Because the hexagon is made up of 6 equilateral triangles, to find the area of the hexagon, we will first find the area of each equilateral triangle then multiply it by 6.

Using the Pythagorean Theorem, we find that the height of each equilateral triangle is  .
.
The area of the triangle is then

Multiply this value by 6 to find the area of the hexagon.
First, let's draw out the hexagon.

Because the hexagon is made up of 6 equilateral triangles, to find the area of the hexagon, we will first find the area of each equilateral triangle then multiply it by 6.

Using the Pythagorean Theorem, we find that the height of each equilateral triangle is 
The area of the triangle is then
Multiply this value by 6 to find the area of the hexagon.
Compare your answer with the correct one above
What is the area of a regular hexagon with a side length of  ?
?
What is the area of a regular hexagon with a side length of 
This question is asking about the area of a regular hexagon that looks like this:

Now, you could proceed by noticing that the hexagon can be divided into little equilateral triangles:

By use of the properties of isosceles and  triangles, you could compute that the area of one of these little triangles is:
triangles, you could compute that the area of one of these little triangles is:
 , where
, where  is the side length. Since there are
is the side length. Since there are  of these triangles, you can multiply this by
of these triangles, you can multiply this by  to get the area of the regular hexagon:
to get the area of the regular hexagon:

It is likely easiest merely to memorize the aforementioned equation for the area of an equilateral triangle. From this, you can derive the hexagon area equation mentioned above. Using this equation and our data, we know:

This question is asking about the area of a regular hexagon that looks like this:

Now, you could proceed by noticing that the hexagon can be divided into little equilateral triangles:

By use of the properties of isosceles and 




It is likely easiest merely to memorize the aforementioned equation for the area of an equilateral triangle. From this, you can derive the hexagon area equation mentioned above. Using this equation and our data, we know:
Compare your answer with the correct one above
What is the area of a regular hexagon with a perimeter of  ?
?
What is the area of a regular hexagon with a perimeter of 
A hexagon has  sides. A regular polygon is one that has sides that are of equal length. Therefore, if the side length of our polygon is taken to be
sides. A regular polygon is one that has sides that are of equal length. Therefore, if the side length of our polygon is taken to be  , we know:
, we know:
 , or
, or 
This question is asking about the area of a regular hexagon that looks like this:

Now, you could proceed by noticing that the hexagon can be divided into little equilateral triangles:

By use of the properties of isosceles and  triangles, you could compute that the area of one of these little triangles is:
triangles, you could compute that the area of one of these little triangles is:
 , where
, where  is the side length. Since there are
is the side length. Since there are  of these triangles, you can multiply this by
of these triangles, you can multiply this by  to get the area of the regular hexagon:
to get the area of the regular hexagon:

It is likely easiest merely to memorize the aforementioned equation for the area of an equilateral triangle. From this, you can derive the hexagon area equation mentioned above. Using this equation and our data, we know:

A hexagon has 


This question is asking about the area of a regular hexagon that looks like this:

Now, you could proceed by noticing that the hexagon can be divided into little equilateral triangles:

By use of the properties of isosceles and 




It is likely easiest merely to memorize the aforementioned equation for the area of an equilateral triangle. From this, you can derive the hexagon area equation mentioned above. Using this equation and our data, we know:
Compare your answer with the correct one above

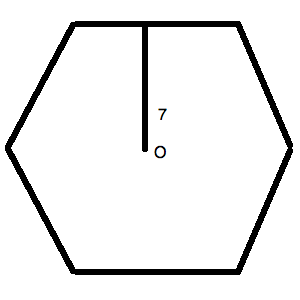
The figure above is a regular hexagon.  is the center of the figure. The line drawn is perpendicular to the side.
is the center of the figure. The line drawn is perpendicular to the side.
What is the area of the figure above?

The figure above is a regular hexagon. 
What is the area of the figure above?
You can redraw the figure given to notice the little equilateral triangle that is formed within the hexagon. Since a hexagon can have the  degrees of its internal rotation divided up evenly, the central angle is
degrees of its internal rotation divided up evenly, the central angle is  degrees. The two angles formed with the sides also are
degrees. The two angles formed with the sides also are  degrees. Thus, you could draw:
degrees. Thus, you could draw:

Now, the  is located on the side that is the same as
is located on the side that is the same as  on your standard
on your standard  triangle. The base of the little triangle formed here is
triangle. The base of the little triangle formed here is  on the standard triangle. Let's call our unknown value
on the standard triangle. Let's call our unknown value  .
.
We know, then, that:

Another way to write  is:
is:

Now, there are several ways you could proceed from here. Notice that there are  of those little triangles in the hexagon. Since you know that the are of a triangle is:
of those little triangles in the hexagon. Since you know that the are of a triangle is:

and for your data...


The area of the whole figure is:

You can redraw the figure given to notice the little equilateral triangle that is formed within the hexagon. Since a hexagon can have the 



Now, the 




We know, then, that:
Another way to write 
Now, there are several ways you could proceed from here. Notice that there are 
and for your data...
The area of the whole figure is:
Compare your answer with the correct one above
What is the area of a regular hexagon with a side length of  miles? Simplify all fractions and square roots in your answer.
miles? Simplify all fractions and square roots in your answer.
What is the area of a regular hexagon with a side length of 
For a hexagon with side length  , the formula for the area is
, the formula for the area is
 .
.
We have a side length of 4 miles, so we plug that into the equation and simplify the fraction.

For a hexagon with side length 

We have a side length of 4 miles, so we plug that into the equation and simplify the fraction.
Compare your answer with the correct one above
What is the area of a hexagon with a side of length two? Simplify all fractions and square roots.
What is the area of a hexagon with a side of length two? Simplify all fractions and square roots.
To find the area of a hexagon with a given side length,  , use the formula:
, use the formula:

Plugging in 2 for  and reducing we get:
and reducing we get:

 . (remember order of operations, square first!)
. (remember order of operations, square first!)
To find the area of a hexagon with a given side length, 
Plugging in 2 for 

Compare your answer with the correct one above
The perimeter of a regular hexagon is  . What is the length of one of its diagonals?
. What is the length of one of its diagonals?
The perimeter of a regular hexagon is 
To begin, calculate the side length of the hexagon. Since it is regular, its sides are of equal length. This means that a given side is  or
or  in length. Now, consider your figure like this:
in length. Now, consider your figure like this:
The little triangle at the top forms an equilateral triangle. This means that all of its sides are  . You could form six of these triangles in your figure if you desired. This means that the long diagonal is really just
. You could form six of these triangles in your figure if you desired. This means that the long diagonal is really just  or
or  .
.
To begin, calculate the side length of the hexagon. Since it is regular, its sides are of equal length. This means that a given side is 


The little triangle at the top forms an equilateral triangle. This means that all of its sides are 


Compare your answer with the correct one above
The figure above is a regular hexagon. O is the center of the figure. The line segment makes a perpendicular angle with the external side.
What is the length of the diagonal of the regular hexagon pictured above?

The figure above is a regular hexagon. O is the center of the figure. The line segment makes a perpendicular angle with the external side.
What is the length of the diagonal of the regular hexagon pictured above?
You could redraw your figure as follows. Notice that this kind of figure makes an equilateral triangle within the hexagon. This allows you to create a useful  triangle.
triangle.

The  in the figure corresponds to
in the figure corresponds to 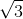 in a reference
in a reference  triangle. The hypotenuse is
triangle. The hypotenuse is  in the reference triangle.
in the reference triangle.
Therefore, we can say:

Solve for  :
:
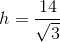
Rationalize the denominator:

Now, the diagonal of a regular hexagon is actually just double the length of this hypotenuse. (You could draw another equilateral triangle on the bottom and duplicate this same calculation set—if you wanted to spend extra time without need!) Thus, the length of the diagonal is:

You could redraw your figure as follows. Notice that this kind of figure makes an equilateral triangle within the hexagon. This allows you to create a useful 

The 
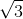


Therefore, we can say:
Solve for 
Rationalize the denominator:
Now, the diagonal of a regular hexagon is actually just double the length of this hypotenuse. (You could draw another equilateral triangle on the bottom and duplicate this same calculation set—if you wanted to spend extra time without need!) Thus, the length of the diagonal is:
Compare your answer with the correct one above
What is the maximum length of each side for a regular hexago with a perimeter of  ?
?
What is the maximum length of each side for a regular hexago with a perimeter of 
Use the formula for perimeter to solve for the side length:



Use the formula for perimeter to solve for the side length:
Compare your answer with the correct one above
Find the length of one side for a regular hexagon with a perimeter of  .
.
Find the length of one side for a regular hexagon with a perimeter of 
Use the formula for perimeter to solve for the side length:



Use the formula for perimeter to solve for the side length:
Compare your answer with the correct one above
Find the length of one side for a regular hexon with a perimeter of  .
.
Find the length of one side for a regular hexon with a perimeter of 
Use the formula for perimeter to solve for the side length:



Use the formula for perimeter to solve for the side length:
Compare your answer with the correct one above
If the perimeter of a regular hexagon is  , what is the length of a side of that regular hexagon?
, what is the length of a side of that regular hexagon?
If the perimeter of a regular hexagon is 
Use the formula for perimeter to solve for the length of a side of the regular hexagon:

Where  is perimeter and
is perimeter and  is the length of a side.
is the length of a side.
In this case:


Use the formula for perimeter to solve for the length of a side of the regular hexagon:
Where 

In this case:
Compare your answer with the correct one above
What is the side of a Hexagon whose area is  ?
?
What is the side of a Hexagon whose area is 
To find the side of a hexagon given the area, set the area formula equal to the given area and solve for the side.

To find the side of a hexagon given the area, set the area formula equal to the given area and solve for the side.
Compare your answer with the correct one above

The figure above is a regular hexagon.  is the center of the figure. The line drawn is perpendicular to the side.
is the center of the figure. The line drawn is perpendicular to the side.
What is the perimeter of the figure above?

The figure above is a regular hexagon. 
What is the perimeter of the figure above?
You can redraw the figure given to notice the little equilateral triangle that is formed within the hexagon. Since a hexagon can have the  degrees of its internal rotation divided up evenly, the central angle is
degrees of its internal rotation divided up evenly, the central angle is  degrees. The two angles formed with the sides also are
degrees. The two angles formed with the sides also are  degrees. Thus, you could draw:
degrees. Thus, you could draw:

Now, the  is located on the side that is the same as
is located on the side that is the same as  on your standard
on your standard  triangle. The base of the little triangle formed here is
triangle. The base of the little triangle formed here is  on the standard triangle. Let's call our unknown value
on the standard triangle. Let's call our unknown value  .
.
We know, then, that:

Or, 
Now, this is only half of the size of the hexagon's side. Therefore, the full side length is  .
.
Since this is a regular hexagon, all of the sides are of equal length. This means that your total perimeter is  or
or  .
.
You can redraw the figure given to notice the little equilateral triangle that is formed within the hexagon. Since a hexagon can have the 



Now, the 




We know, then, that:
Or,
Now, this is only half of the size of the hexagon's side. Therefore, the full side length is 
Since this is a regular hexagon, all of the sides are of equal length. This means that your total perimeter is 

Compare your answer with the correct one above